1 . 已知数列 满足
满足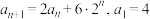 .
.
(1)证明数列 为等差数列,并求
为等差数列,并求 ;
;
(2)求数列 的前
的前 项和
项和 .
.
 满足
满足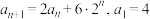 .
.(1)证明数列
 为等差数列,并求
为等差数列,并求 ;
;(2)求数列
 的前
的前 项和
项和 .
.
您最近一年使用:0次
2024-01-25更新
|
1517次组卷
|
4卷引用:广东省深圳市龙岗区2023-2024学年高二上学期1月期末质量监测数学试题
广东省深圳市龙岗区2023-2024学年高二上学期1月期末质量监测数学试题广东省广州市广东实验中学2024届高三上学期第二次调研数学试题(已下线)第五章:数列(单元测试)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)江苏省南京市田家炳高级中学2023-2024学年高二下学期期中考试数学试卷
2 . 已知数列{an}满足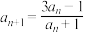 ,
, ,令
,令 .
.
(1)证明:数列 是等差数列;
是等差数列;
(2)求数列 的通项公式.
的通项公式.
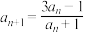 ,
, ,令
,令 .
.(1)证明:数列
 是等差数列;
是等差数列;(2)求数列
 的通项公式.
的通项公式.
您最近一年使用:0次
2023-12-13更新
|
511次组卷
|
4卷引用:广东省汕头市潮阳实验学校2023-2024学年高二上学期第二次月考数学试题
广东省汕头市潮阳实验学校2023-2024学年高二上学期第二次月考数学试题(已下线)4.2.1&4.2.2 等差数列的概念与等差数列的通项公式(8大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)(已下线)5.2.1 等差数列(4知识点+8题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)(已下线)4.2.1 等差数列的概念(分层练习)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第二册)
22-23高二上·福建漳州·期中
名校
解题方法
3 . 设数列 的各项都为正数,且
的各项都为正数,且 .
.
(1)证明数列 为等差数列;
为等差数列;
(2)设 ,求数列
,求数列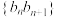 的前
的前 项和
项和 .
.
 的各项都为正数,且
的各项都为正数,且 .
.(1)证明数列
 为等差数列;
为等差数列;(2)设
 ,求数列
,求数列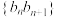 的前
的前 项和
项和 .
.
您最近一年使用:0次
2023-09-30更新
|
2570次组卷
|
9卷引用:广东省广州市第九十七中学2024届高三上学期10月月考数学试题
(已下线)广东省广州市第九十七中学2024届高三上学期10月月考数学试题福建省诏安县桥东中学2022-2023学年高二上学期期中考试数学试题甘肃省兰州市教育局第四片区联考2023-2024学年高二上学期期中考试数学试题辽宁省六校协作体2024届高三上学期期中联考数学试题(已下线)第4章 数列 章末题型归纳总结(2)(已下线)第09讲 第四章 数列 章节验收测评卷(综合卷)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第二册)(已下线)热点5-1 等差数列的通项及前n项和(8题型+满分技巧+限时检测)(已下线)第4章 数列单元检测(基础卷)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)(已下线)4.2.2 等差数列的前n项和公式——随堂检测
名校
解题方法
4 . 马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…,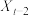 ,
,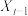 ,
,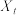 ,
, ,…,那么
,…,那么 时刻的状态的条件概率仅依赖前一状态
时刻的状态的条件概率仅依赖前一状态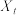 ,即
,即 .
.
现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为 ,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 ,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为
,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为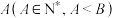 ,赌博过程如下图的数轴所示.
,赌博过程如下图的数轴所示. ,
, )时,
)时,最终输光的概率为 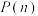 ,请回答下列问题:
,请回答下列问题:
(1)请直接写出 与
与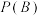 的数值.
的数值.
(2)证明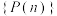 是一个等差数列,并写出公差d.
是一个等差数列,并写出公差d.
(3)当 时,分别计算
时,分别计算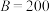 ,
, 时,
时,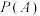 的数值,并结合实际,解释当
的数值,并结合实际,解释当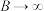 时,
时,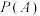 的统计含义.
的统计含义.
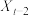 ,
,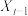 ,
,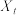 ,
, ,…,那么
,…,那么 时刻的状态的条件概率仅依赖前一状态
时刻的状态的条件概率仅依赖前一状态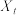 ,即
,即 .
.现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为
 ,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 ,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为
,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为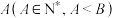 ,赌博过程如下图的数轴所示.
,赌博过程如下图的数轴所示.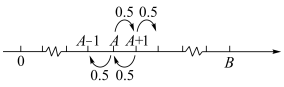
 ,
, )时,
)时,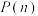 ,请回答下列问题:
,请回答下列问题:(1)请直接写出
 与
与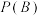 的数值.
的数值.(2)证明
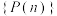 是一个等差数列,并写出公差d.
是一个等差数列,并写出公差d.(3)当
 时,分别计算
时,分别计算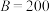 ,
, 时,
时,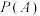 的数值,并结合实际,解释当
的数值,并结合实际,解释当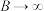 时,
时,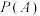 的统计含义.
的统计含义.
您最近一年使用:0次
2023-04-06更新
|
10638次组卷
|
20卷引用:广东省佛山市南海区第一中学2024届高三上学期10月月考数学试题
广东省佛山市南海区第一中学2024届高三上学期10月月考数学试题浙江省杭州市2023届高三下学期教学质量检测(二模)数学试题(已下线)专题10 计数原理与概率统计(理科)(已下线)模块二 专题4 条件概率与全概率公式(已下线)专题08 概率统计及计数原理(已下线)押新高考第19题 概率统计江西省景德镇一中2022-2023学年高二(19班)下学期期中考试数学试题湖南师范大学附属中学2023届高三三模数学试题(已下线)第四篇 概率与统计 专题6 随机游走与马尔科夫过程 微点1 随机游走与马尔科夫链(已下线)重难点突破01 概率与统计的综合应用(十八大题型)-3(已下线)概 率辽宁省沈阳市第二中学2024届高三下学期开学考试数学试题专题14条件概率与全概率公式(已下线)专题03 条件概率与全概率公式(2)(已下线)专题04 概率统计大题(已下线)专题8-2分布列综合归类-2(已下线)湖南省郴州市2024届高三一模数学试题变式题17-22(已下线)专题6 全概率与数列结合问题河南省信阳市新县高级中学2024届高三下学期适应性考试(八)数学试题单元测试B卷——第七章 随机变量及其分布
解题方法
5 . 已知数列 的前
的前 项和为
项和为 ,且
,且
(1)求 ,并证明数列
,并证明数列 是等差数列:
是等差数列:
(2)若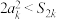 ,求正整数
,求正整数 的所有取值.
的所有取值.
 的前
的前 项和为
项和为 ,且
,且
(1)求
 ,并证明数列
,并证明数列 是等差数列:
是等差数列:(2)若
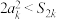 ,求正整数
,求正整数 的所有取值.
的所有取值.
您最近一年使用:0次
2023-03-14更新
|
4520次组卷
|
5卷引用:广东省广州市2023届高三综合测试(一)数学试题
广东省广州市2023届高三综合测试(一)数学试题专题13数列(解答题)云南省文山州广南县第一中学校2024届高三上学期第一次省统测数学模拟试题江苏省扬州市宝应县2024届高三上学期期末模拟数学试题(已下线)第4章 数列单元测试基础卷-2023-2024学年高二上学期数学人教A版(2019)选择性必修第二册
解题方法
6 . 已知数列 中
中 ,其前
,其前 项和记为
项和记为 ,且满足
,且满足 .
.
(1)求数列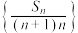 的通项公式;
的通项公式;
(2)设无穷数列 ,
, ,…
,… ,…对任意自然数
,…对任意自然数 和
和 ,不等式
,不等式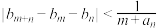 均成立,证明:数列
均成立,证明:数列 是等差数列.
是等差数列.
 中
中 ,其前
,其前 项和记为
项和记为 ,且满足
,且满足 .
.(1)求数列
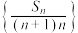 的通项公式;
的通项公式;(2)设无穷数列
 ,
, ,…
,… ,…对任意自然数
,…对任意自然数 和
和 ,不等式
,不等式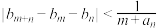 均成立,证明:数列
均成立,证明:数列 是等差数列.
是等差数列.
您最近一年使用:0次
2023-03-16更新
|
636次组卷
|
3卷引用:广东省韶关市武江区广东北江实验学校2022-2023学年高二下学期第一次(3月)月考数学试题
广东省韶关市武江区广东北江实验学校2022-2023学年高二下学期第一次(3月)月考数学试题江苏省南京市中华、东外、镇江三校2022-2023学年高三下学期3月联考数学试题(已下线)第4章 数列 单元综合检测(重点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
名校
解题方法
7 . 已知正项数列 的前
的前 项和为
项和为 ,且满足
,且满足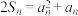 .
.
(1)求数列
 的通项公式;
的通项公式;(2)设
 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: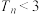 .
.
您最近一年使用:0次
2022-11-12更新
|
1950次组卷
|
10卷引用:广东省肇庆市2023届高三上学期第一次教学质量检测数学试题
广东省肇庆市2023届高三上学期第一次教学质量检测数学试题广东省梅州市平远县平远中学2022-2023学年高三上学期期末考试数学试题广东省韶关市南雄中学2023届高三下学期4月月考数学试题广东省惠州市博罗县博师高级中学2024届高三上学期9月月考数学试题(已下线)4.2 等差数列(5)湖南省2023届高三下学期3月联考数学试题安徽省马鞍山市第二中学2022-2023学年高二下学期期中模拟测试(B)数学试题湖南省长沙市雅礼中学2024届高三上学期月考(二)数学试题(已下线)湖南省长沙市雅礼中学2024届高三上学期月考(二)数学试题变式题15-18湖南省株洲市第一中学2022届高三上学期期中数学试题
8 . 已知等差数列 满足
满足 ,
,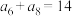 ,等比数列
,等比数列 满足
满足 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)令 ,求证:
,求证: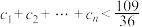 ,其中
,其中 .
.
 满足
满足 ,
,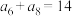 ,等比数列
,等比数列 满足
满足 ,
, .
.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)令
 ,求证:
,求证: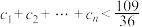 ,其中
,其中 .
.
您最近一年使用:0次
2022-11-24更新
|
888次组卷
|
3卷引用:广东省佛山市第一中学2023届高三上学期第三次月考数学试题
9 . 已知数列 满足
满足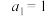 ,
, ,令
,令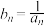 ,设数列
,设数列 前n项和为
前n项和为 .
.
(1)求证:数列 为等差数列;
为等差数列;
(2)若存在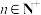 ,使不等式
,使不等式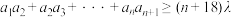 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)设正项数列 满足
满足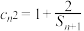 ,求证:
,求证: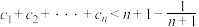 .
.
 满足
满足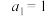 ,
, ,令
,令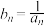 ,设数列
,设数列 前n项和为
前n项和为 .
.(1)求证:数列
 为等差数列;
为等差数列;(2)若存在
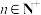 ,使不等式
,使不等式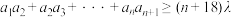 成立,求实数
成立,求实数 的取值范围;
的取值范围;(3)设正项数列
 满足
满足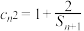 ,求证:
,求证: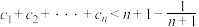 .
.
您最近一年使用:0次
2022-07-21更新
|
1578次组卷
|
7卷引用:广东省广东实验中学2023届高三上学期第一次段考数学试题
广东省广东实验中学2023届高三上学期第一次段考数学试题四川省眉山市2021-2022学年高一下学期期末数学(理)试题(已下线)4.2.3 等差数列的前n项和-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)(已下线)4.2.2.2 等差数列的前n项和的性质及应用(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第二册)(已下线)专题15 数列不等式的证明 微点6 数列不等式的证明综合训练(已下线)数列与不等式(已下线)4.1 等差数列(第2课时)(十三大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
10 . 设数列 的前
的前 项和为
项和为 ,已知
,已知 ,__________.
,__________.
(1)求数列 的通项公式;
的通项公式;
(2)设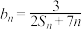 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
从下列两个条件中任选一个作为已知,补充在上面问题的横线中进行求解(若两个都选,则按所写的第1个评分):
①数列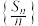 是以
是以 为公差的等差数列;②
为公差的等差数列;② .
.
 的前
的前 项和为
项和为 ,已知
,已知 ,__________.
,__________.(1)求数列
 的通项公式;
的通项公式;(2)设
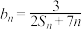 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.从下列两个条件中任选一个作为已知,补充在上面问题的横线中进行求解(若两个都选,则按所写的第1个评分):
①数列
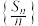 是以
是以 为公差的等差数列;②
为公差的等差数列;② .
.
您最近一年使用:0次
2022-11-03更新
|
744次组卷
|
6卷引用:广东省佛山市顺德区2023届高三上学期教学质量检测(一)数学试题
广东省佛山市顺德区2023届高三上学期教学质量检测(一)数学试题江西省丰城中学2023届高三上学期第四次段考数学(理)试题(已下线)第4章 数列 单元综合检测-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)(已下线)第4章 数列 单元综合检测(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第二册)江苏省淮安市高中校协作体2024届高三上学期期中联考数学试题(已下线)技巧04 结构不良问题解题策略(5大核心考点)(讲义)



