1 . 已知数列 的前
的前 项和为
项和为 ,且
,且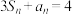 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,且数列
,且数列 的前
的前 项和为
项和为 ,若
,若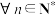 都有不等式
都有不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 的前
的前 项和为
项和为 ,且
,且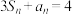 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,且数列
,且数列 的前
的前 项和为
项和为 ,若
,若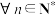 都有不等式
都有不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-26更新
|
1486次组卷
|
6卷引用:福建省南平市2023-2024学年高二上学期期末数学试题
福建省南平市2023-2024学年高二上学期期末数学试题黑龙江省实验中学2023-2024学年高二下学期4月考数学试题(已下线)专题04数列求和的6种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(北师大版2019选择性必修第二册)(已下线)专题03数列期末7种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(人教B版2019选择性必修第三册)江西省临川第二中学2023-2024学年高二下学期6月月考数学试题四川省江油市太白中学2023-2024学年高二下学期期中考试数学试题
名校
2 . 某人从 地到
地到 地有路程接近的2条路线可以选择,其中第一条路线上有
地有路程接近的2条路线可以选择,其中第一条路线上有 个路口,第二条路线上有
个路口,第二条路线上有 个路口.
个路口.
(1)若 ,
, ,第一条路线的每个路口遇到红灯的概率均为
,第一条路线的每个路口遇到红灯的概率均为 ;第二条路线的第一个路口遇到红灯的概率为
;第二条路线的第一个路口遇到红灯的概率为 ,第二个路口遇到红灯的概率为
,第二个路口遇到红灯的概率为 ,从“遇到红灯次数的期望”考虑,哪条路线更好?请说明理由.
,从“遇到红灯次数的期望”考虑,哪条路线更好?请说明理由.
(2)已知;随机变量 服从两点分布,且
服从两点分布,且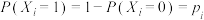 ,.则
,.则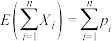 ,且
,且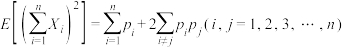 .若第一条路线的第
.若第一条路线的第 个路口遇到红灯的概率为
个路口遇到红灯的概率为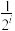 ,当选择第一条路线时,求遇到红灯次数的方差.
,当选择第一条路线时,求遇到红灯次数的方差.
 地到
地到 地有路程接近的2条路线可以选择,其中第一条路线上有
地有路程接近的2条路线可以选择,其中第一条路线上有 个路口,第二条路线上有
个路口,第二条路线上有 个路口.
个路口.(1)若
 ,
, ,第一条路线的每个路口遇到红灯的概率均为
,第一条路线的每个路口遇到红灯的概率均为 ;第二条路线的第一个路口遇到红灯的概率为
;第二条路线的第一个路口遇到红灯的概率为 ,第二个路口遇到红灯的概率为
,第二个路口遇到红灯的概率为 ,从“遇到红灯次数的期望”考虑,哪条路线更好?请说明理由.
,从“遇到红灯次数的期望”考虑,哪条路线更好?请说明理由.(2)已知;随机变量
 服从两点分布,且
服从两点分布,且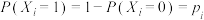 ,.则
,.则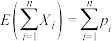 ,且
,且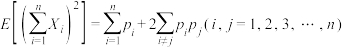 .若第一条路线的第
.若第一条路线的第 个路口遇到红灯的概率为
个路口遇到红灯的概率为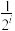 ,当选择第一条路线时,求遇到红灯次数的方差.
,当选择第一条路线时,求遇到红灯次数的方差.
您最近一年使用:0次
2024-01-22更新
|
956次组卷
|
6卷引用:福建省南平市浦城县2023-2024学年高二下学期4月期中考试数学试题
名校
解题方法
3 . 已知等比数列 公比为q,前n项和为
公比为q,前n项和为 ,且满足
,且满足 ,则( )
,则( )
 公比为q,前n项和为
公比为q,前n项和为 ,且满足
,且满足 ,则( )
,则( )A. | B.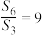 |
C. , ,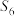 , , 成等比数列 成等比数列 | D. |
您最近一年使用:0次
2023-12-14更新
|
521次组卷
|
3卷引用:福建省南平第一中学2023-2024学年高二上学期第三次月考数学试卷
福建省南平第一中学2023-2024学年高二上学期第三次月考数学试卷湖南省衡阳市衡阳县第二中学2023-2024学年高二上学期期末达标测试数学试题(B卷)(已下线)专题07 等比数列及其前n项和6种常见考法归类(3)
4 . 记 为数列
为数列 的前
的前 项和,
项和, 为数列
为数列 的前
的前 项和,若
项和,若 且
且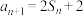 .
.
(1)证明:数列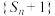 是等比数列;
是等比数列;
(2)若 成立,求
成立,求 的最小值.
的最小值.
 为数列
为数列 的前
的前 项和,
项和, 为数列
为数列 的前
的前 项和,若
项和,若 且
且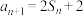 .
.(1)证明:数列
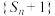 是等比数列;
是等比数列;(2)若
 成立,求
成立,求 的最小值.
的最小值.
您最近一年使用:0次
2023-10-02更新
|
846次组卷
|
3卷引用:福建省南平市建阳第二中学2024届高三上学期第二次月考数学试题
名校
解题方法
5 . 已知数列 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, ,
, .
.(1)求数列
 、
、 的通项公式;
的通项公式;(2)设
 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
您最近一年使用:0次
2022-06-02更新
|
1318次组卷
|
4卷引用:福建省南平第一中学2023-2024学年高二上学期第三次月考数学试卷
解题方法
6 . 已知数列 满足对任意的正整数n,都有
满足对任意的正整数n,都有 ,其中
,其中 ,则数列
,则数列 的前2022项和是( )
的前2022项和是( )
 满足对任意的正整数n,都有
满足对任意的正整数n,都有 ,其中
,其中 ,则数列
,则数列 的前2022项和是( )
的前2022项和是( )A.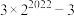 | B.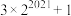 | C. | D.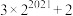 |
您最近一年使用:0次
2022-03-07更新
|
707次组卷
|
3卷引用:福建省南平市浦城县第三中学2023届高三上学期数学期中测试模拟卷试题(3)
福建省南平市浦城县第三中学2023届高三上学期数学期中测试模拟卷试题(3)三省三校(黑龙江哈师大附中、东北师大附中、辽宁实验中学)2022届高三下学期第一次模拟数学(理)试题(已下线)三省三校2022届高三下学期第一次模拟数学(理)试题变式题6-10
7 . 若数列 的各项均为正数,且满足
的各项均为正数,且满足 ,
,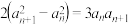 ,则数列
,则数列 的前6项和为
的前6项和为_______ .
 的各项均为正数,且满足
的各项均为正数,且满足 ,
,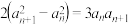 ,则数列
,则数列 的前6项和为
的前6项和为
您最近一年使用:0次
8 . 已知数列 满足
满足 ,
,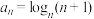
 .定义:使乘积
.定义:使乘积 为正整数的
为正整数的
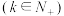 叫做“幸运数”,则在
叫做“幸运数”,则在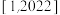 内的所有“幸运数”的和为
内的所有“幸运数”的和为________ .
 满足
满足 ,
,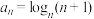
 .定义:使乘积
.定义:使乘积 为正整数的
为正整数的
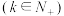 叫做“幸运数”,则在
叫做“幸运数”,则在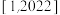 内的所有“幸运数”的和为
内的所有“幸运数”的和为
您最近一年使用:0次
9 . 已知数列 的前
的前 项和是
项和是 ,且
,且
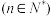 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设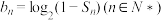 ,
,
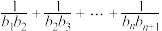 ,求
,求 的取值范围.
的取值范围.
 的前
的前 项和是
项和是 ,且
,且
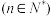 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
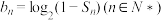 ,
,
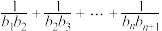 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-08-24更新
|
302次组卷
|
3卷引用:福建省南平市浦城县2021届高三上学期期中测试数学试题
名校
解题方法
10 . 已知数列 的前n项和
的前n项和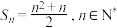 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和.
项和.
 的前n项和
的前n项和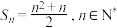 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前 项和.
项和.
您最近一年使用:0次
2021-09-03更新
|
722次组卷
|
15卷引用:福建省建瓯市芝华中学2023届高三上学期暑期考试数学试题
福建省建瓯市芝华中学2023届高三上学期暑期考试数学试题2016-2017学年重庆市高一春季九校联考数学(文)试卷(已下线)测试卷38 数列(B)-2021届高考数学一轮复习(文理通用)单元过关测试卷(已下线)4.3.2 等比数列的前n项和公式(第1课时)(练习)-2020-2021学年上学期高二数学同步精品课堂(新教材人教版选择性必修第二册)广西钦州市大寺中学2020-2021学年高一下学期期中考试数学试题(已下线)专题04 数列求和(知识串讲)-2020-2021学年高二数学重难点手册(数列篇,人教A版2019选择性必修第二册)重庆市第十一中学2021届高三下学期5月月考数学试题山西省运城市平陆中学2021-2022学年高二上学期开学测试数学试题广西南宁市第十九中学2023届高三上学期数学(文)信息卷(三)试题陕西省汉中市城固县2021-2022学年高三上学期调研检测理科数学试题福建省莆田第十五中学、二十四中学2021-2022学年高二上学期期末联考数学试题新疆柯坪县柯坪湖州国庆中学2023届高三上学期期末考试数学(文)试题河北省衡水市武邑中学2024届高三上学期第三次调研考试数学试题(已下线)第四章 数列(压轴题专练)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第一册)(已下线)专题21 数列解答题(文科)-2



