2024·全国·模拟预测
解题方法
1 . 在四棱锥 中,已知底面
中,已知底面 为正方形,平面
为正方形,平面 、平面
、平面 都与平面
都与平面 垂直,
垂直,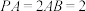 ,点
,点 分别为
分别为 的中点,点
的中点,点 在棱
在棱 上,则( )
上,则( )
 中,已知底面
中,已知底面 为正方形,平面
为正方形,平面 、平面
、平面 都与平面
都与平面 垂直,
垂直,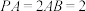 ,点
,点 分别为
分别为 的中点,点
的中点,点 在棱
在棱 上,则( )
上,则( )| A.四边形BCTS为等腰梯形 |
B.不存在点 ,使得 ,使得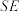 ∥平面 ∥平面 |
C.存在点 ,使得 ,使得 |
D.点 到 到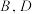 两点的距离和的最小值为 两点的距离和的最小值为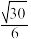 |
您最近半年使用:0次
2024·全国·模拟预测
解题方法
2 . 在四棱锥 中,底面
中,底面 为正方形,平面
为正方形,平面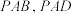 都与平面
都与平面 垂直,
垂直,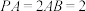 ,点
,点 分别为
分别为 的中点,且
的中点,且 是线段
是线段 上一点(包含端点),给出下列结论:①四边形
上一点(包含端点),给出下列结论:①四边形 为等腰梯形;②不存在点
为等腰梯形;②不存在点 ,使得
,使得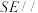 平面
平面 ;③存在点
;③存在点 ,使得
,使得 ;④
;④ 的最小值为
的最小值为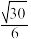 .其中所有正确结论的序号为
.其中所有正确结论的序号为______ .
 中,底面
中,底面 为正方形,平面
为正方形,平面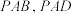 都与平面
都与平面 垂直,
垂直,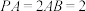 ,点
,点 分别为
分别为 的中点,且
的中点,且 是线段
是线段 上一点(包含端点),给出下列结论:①四边形
上一点(包含端点),给出下列结论:①四边形 为等腰梯形;②不存在点
为等腰梯形;②不存在点 ,使得
,使得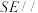 平面
平面 ;③存在点
;③存在点 ,使得
,使得 ;④
;④ 的最小值为
的最小值为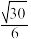 .其中所有正确结论的序号为
.其中所有正确结论的序号为
您最近半年使用:0次
3 . 如图,已知正三棱锥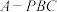 和正三棱锥
和正三棱锥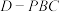 的侧棱长均为
的侧棱长均为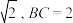 .若将正三棱锥
.若将正三棱锥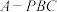 绕
绕 旋转,使得点
旋转,使得点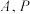 分别旋转至点
分别旋转至点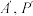 处,且
处,且 四点共面,点
四点共面,点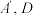 分别位于
分别位于 两侧,则下列说法中正确的是( )
两侧,则下列说法中正确的是( )
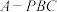 和正三棱锥
和正三棱锥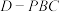 的侧棱长均为
的侧棱长均为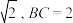 .若将正三棱锥
.若将正三棱锥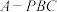 绕
绕 旋转,使得点
旋转,使得点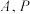 分别旋转至点
分别旋转至点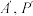 处,且
处,且 四点共面,点
四点共面,点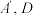 分别位于
分别位于 两侧,则下列说法中正确的是( )
两侧,则下列说法中正确的是( )
A.多面体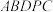 存在外接球 存在外接球 | B.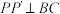 |
C.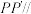 平面 平面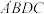 | D.点 运动所形成的最短轨迹长大于 运动所形成的最短轨迹长大于 |
您最近半年使用:0次
4 . 在直四棱柱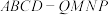 中,底面
中,底面 为平行四边形,
为平行四边形,  ,
,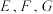 分别为线段
分别为线段 的中点.
的中点.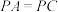 ;
;
(2)证明:平面 //平面
//平面 ;
;
(3)若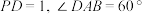 ,当
,当 与平面
与平面 所成角的正弦值最大时,求四棱锥
所成角的正弦值最大时,求四棱锥 的体积.
的体积.
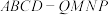 中,底面
中,底面 为平行四边形,
为平行四边形,  ,
,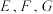 分别为线段
分别为线段 的中点.
的中点.
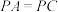 ;
;(2)证明:平面
 //平面
//平面 ;
;(3)若
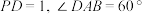 ,当
,当 与平面
与平面 所成角的正弦值最大时,求四棱锥
所成角的正弦值最大时,求四棱锥 的体积.
的体积.
您最近半年使用:0次
解题方法
5 . 如图,在棱长为 的正方体
的正方体 中,已知
中,已知 ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,点
的中点,点 满足
满足 ,
, ,下列说法正确的是
,下列说法正确的是 ( )
( )
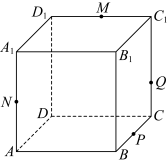
A.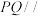 平面 平面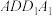 |
B.若 , , , , , , 四点共面,则 四点共面,则 |
C.若 ,点 ,点 在侧面 在侧面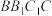 内,且 内,且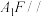 平面 平面 ,则点 ,则点 的轨迹长度为 的轨迹长度为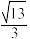 |
D.若 ,由平面 ,由平面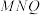 分割该正方体所成的两个空间几何体为 分割该正方体所成的两个空间几何体为 和 和 ,某球能够被整体放入 ,某球能够被整体放入 或 或 ,则该球的表面积最大值为 ,则该球的表面积最大值为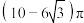 |
您最近半年使用:0次
名校
解题方法
6 . 在正方体 中,
中, 为
为 的中点,
的中点, 在棱
在棱 上,且
上,且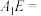
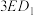 ,则过
,则过 且与
且与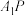 垂直的平面截正方体
垂直的平面截正方体 所得截面的面积为( )
所得截面的面积为( )
 中,
中, 为
为 的中点,
的中点, 在棱
在棱 上,且
上,且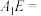
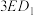 ,则过
,则过 且与
且与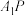 垂直的平面截正方体
垂直的平面截正方体 所得截面的面积为( )
所得截面的面积为( )| A.6 | B.8 | C.12 | D.16 |
您最近半年使用:0次
7 . 半正多面体亦称“阿基米德体”“阿基米德多面体”,是由边数不全相同的正多边形为面围成的多面体.某半正多面体由6个正方形和8个正六边形构成,其也可由正八面体(由八个等边三角形构成,也可以看作上、下两个正四棱锥黏合而成)切割而成.在如图所示的半正多面体中,若其棱长为1,则下列结论正确的是( )
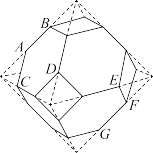
A.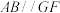 |
B.若平面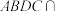 平面 平面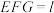 ,则 ,则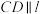 |
C.该半正多面体的体积为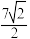 |
D.该半正多面体的表面积为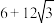 |
您最近半年使用:0次
2024-04-28更新
|
376次组卷
|
2卷引用:河北省沧州市沧衡学校联盟2023-2024学年高一下学期4月期中考试数学试题
名校
解题方法
8 . 如图,在正方体 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 上的动点,且
上的动点,且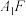
 平面
平面 .设
.设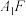 与平面
与平面 所成的角为
所成的角为 与
与 所成的角为
所成的角为 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 上的动点,且
上的动点,且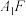
 平面
平面 .设
.设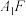 与平面
与平面 所成的角为
所成的角为 与
与 所成的角为
所成的角为 ,那么下列结论正确的是( )
,那么下列结论正确的是( )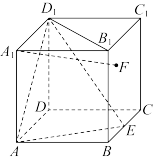
A. 的最小值为 的最小值为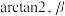 的最小值为 的最小值为 |
B. 的最小值为 的最小值为 的最大值为 的最大值为 |
C. 的最小值大于 的最小值大于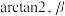 的最小值大于 的最小值大于 |
D. 的最大值小于 的最大值小于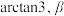 的最大值小于 的最大值小于 |
您最近半年使用:0次
9 . 正三棱柱 的底面边长是4,侧棱长是6,
的底面边长是4,侧棱长是6, ,
, 分别为
分别为 ,
, 的中点,若
的中点,若 是侧面
是侧面 上一点,且
上一点,且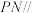 平面
平面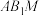 ,则线段
,则线段 的最小值为
的最小值为______ .
 的底面边长是4,侧棱长是6,
的底面边长是4,侧棱长是6, ,
, 分别为
分别为 ,
, 的中点,若
的中点,若 是侧面
是侧面 上一点,且
上一点,且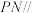 平面
平面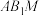 ,则线段
,则线段 的最小值为
的最小值为
您最近半年使用:0次
解题方法
10 . 在长方体 中,已知
中,已知 ,点
,点 满足
满足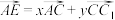 ,其中
,其中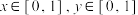 ,则( )
,则( )
 中,已知
中,已知 ,点
,点 满足
满足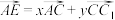 ,其中
,其中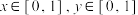 ,则( )
,则( )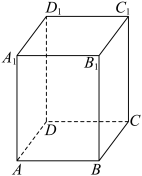
A.当 时, 时,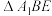 的周长为定值 的周长为定值 |
B.当 时,三棱锥 时,三棱锥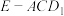 的体积为定值 的体积为定值 |
C.当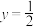 时,有且仅有一个点 时,有且仅有一个点 使得 使得 |
D.当 时,三棱锥 时,三棱锥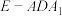 的外接球表面积的最小值为 的外接球表面积的最小值为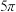 |
您最近半年使用:0次



