解题方法
1 . 在长方体 中,
中, ,
, ,
,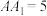 ,则
,则 与平面
与平面 所成角的正切值为
所成角的正切值为__________ .
 中,
中, ,
, ,
,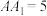 ,则
,则 与平面
与平面 所成角的正切值为
所成角的正切值为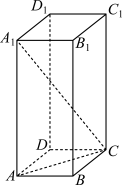
您最近一年使用:0次
2023-08-10更新
|
449次组卷
|
3卷引用:江西省宜春市丰城市第九中学2022-2023学年高一下学期期末考试数学试题
江西省宜春市丰城市第九中学2022-2023学年高一下学期期末考试数学试题(已下线)江西省宜春市丰城市东煌学校2023-2024学年高一下学期期末考试数学试题吉林省辽源市田家炳高级中学校2022-2023学年高一下学期6月月考数学试题
名校
解题方法
2 . 如图,在直四棱柱 中,当底面ABCD满足条件
中,当底面ABCD满足条件___________ 时,有 .(只需填写一种正确条件即可)
.(只需填写一种正确条件即可)
 中,当底面ABCD满足条件
中,当底面ABCD满足条件 .(只需填写一种正确条件即可)
.(只需填写一种正确条件即可)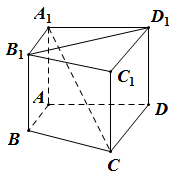
您最近一年使用:0次
2021-12-21更新
|
1212次组卷
|
9卷引用:江西省南昌市豫章中学2024届高三下学期5月模拟(三模)数学试题(B卷)
江西省南昌市豫章中学2024届高三下学期5月模拟(三模)数学试题(B卷)北京市北京理工大学附属中学2021-2022学年高二12月月考数学试题宁夏银川唐徕回民中学2021-2022学年高一上学期期末考试数学试题(已下线)13.2.3直线与平面位置关系(2)线面垂直的判定与性质(备作业)-【上好课】2021-2022学年高一数学同步备课系列(苏教版2019必修第二册)(已下线)第04讲 空间直线、平面的垂直 (高频考点—精练)(已下线)广东省2022届高三一模数学试题变式题11-16(已下线)模块四 专题1 小题入门夯实练(3)(人教B)(已下线)第一章 点线面位置关系 专题二 空间垂直关系的判定与证明 微点4 空间垂直关系的判定与证明综合训练【培优版】(已下线)核心考点8 立体几何中综合问题 A基础卷 (高一期末考试必考的10大核心考点)
名校
解题方法
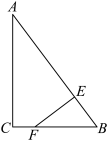
3 . 在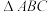 中,
中, ,
,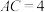 ,
,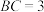 ,
, 为线段
为线段 上的一点(不与端点
上的一点(不与端点 重合),
重合), 交线段
交线段 于
于 (不与端点
(不与端点 重合),将
重合),将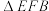 沿
沿 向上折起,使得平面
向上折起,使得平面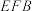 垂直于平面
垂直于平面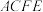 ,则四棱锥
,则四棱锥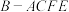 的体积的最大值为
的体积的最大值为__________ .
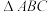 中,
中, ,
,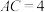 ,
,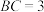 ,
, 为线段
为线段 上的一点(不与端点
上的一点(不与端点 重合),
重合), 交线段
交线段 于
于 (不与端点
(不与端点 重合),将
重合),将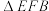 沿
沿 向上折起,使得平面
向上折起,使得平面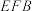 垂直于平面
垂直于平面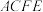 ,则四棱锥
,则四棱锥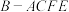 的体积的最大值为
的体积的最大值为
您最近一年使用:0次
4 . 如图,正方体 的棱长为
的棱长为 ,动点
,动点 在线段
在线段 上,
上, 、
、 分别是
分别是 、
、 的中点,则下列结论中正确的是
的中点,则下列结论中正确的是______________ . 与
与 所成角为
所成角为 ;
;
② 平面
平面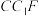 ;
;
③存在点 ,使得平面
,使得平面 平面
平面 ;
;
④三棱锥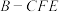 的体积为定值.
的体积为定值.
 的棱长为
的棱长为 ,动点
,动点 在线段
在线段 上,
上, 、
、 分别是
分别是 、
、 的中点,则下列结论中正确的是
的中点,则下列结论中正确的是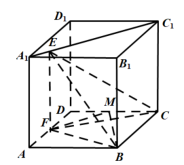
 与
与 所成角为
所成角为 ;
;②
 平面
平面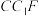 ;
;③存在点
 ,使得平面
,使得平面 平面
平面 ;
;④三棱锥
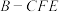 的体积为定值.
的体积为定值.
您最近一年使用:0次
2020-03-20更新
|
1392次组卷
|
5卷引用:2020届江西省南城县第一中学高三上学期期末考试数学(文)试题
2020届江西省南城县第一中学高三上学期期末考试数学(文)试题(已下线)【新教材精创】11.4.1直线与平面垂直(第1课时)练习(2)宁夏石嘴山市第三中学2022-2023学年高一下学期期末数学试题(已下线)高一下学期期末复习填空题压轴题二十三大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)【高一模块一】难度5 小题强化限时晋级练 (中等2)
名校
解题方法
5 . 如图,菱形 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,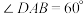 ,
, 和
和 交于点
交于点 ,
, ,点
,点 为线段
为线段 上任意一点,直线
上任意一点,直线 与平面
与平面 所成角为
所成角为 ,则
,则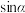 的取值范围
的取值范围______ .
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,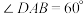 ,
, 和
和 交于点
交于点 ,
, ,点
,点 为线段
为线段 上任意一点,直线
上任意一点,直线 与平面
与平面 所成角为
所成角为 ,则
,则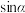 的取值范围
的取值范围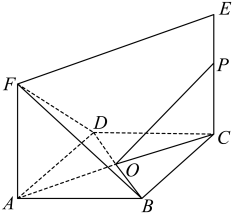
您最近一年使用:0次
2020-02-09更新
|
623次组卷
|
3卷引用:江西省临川第一中学2023-2024学年高二上学期期末数学试题
江西省临川第一中学2023-2024学年高二上学期期末数学试题浙江省金华十校2019-2020学年高二上学期期末考试数学试题(已下线)第二章 立体几何中的计算 专题一 空间角 微点3 直线与平面所成角(一)【基础版】
6 . 如图所示,正方体 的棱长为
的棱长为 ,线段
,线段 上有两个动点
上有两个动点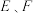 ,且
,且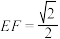 ,则下列结论中正确的是
,则下列结论中正确的是_____ .
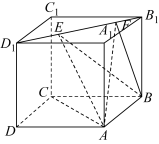
① ∥平面
∥平面 ;
;
②平面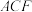 ⊥平面
⊥平面 ;
;
③三棱锥 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线 与
与 成角
成角 °.
°.
 的棱长为
的棱长为 ,线段
,线段 上有两个动点
上有两个动点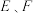 ,且
,且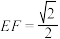 ,则下列结论中正确的是
,则下列结论中正确的是
①
 ∥平面
∥平面 ;
;②平面
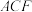 ⊥平面
⊥平面 ;
;③三棱锥
 的体积为定值;
的体积为定值;④存在某个位置使得异面直线
 与
与 成角
成角 °.
°.
您最近一年使用:0次
2019-06-07更新
|
678次组卷
|
7卷引用:江西省赣州市于都县第三中学、全南县第二中学2017-2018学年高一上学期期末联考数学试题
江西省赣州市于都县第三中学、全南县第二中学2017-2018学年高一上学期期末联考数学试题【市级联考】江西省新余市2017-2018学年高一上学期期末考试数学试题江西省抚州市金溪县第一中学2021-2022学年高二上学期第一次月考数学(文)试题【校级联考】福建省宁德市高中同心顺联盟校2018-2019学年高一下学期期中考试数学试题北京大学附中石景山学校2019-2020学年高二上学期期中数学试题(已下线)专题07立体几何线面位置关系(练)(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题07立体几何线面位置关系(练)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)



