2022高三·全国·专题练习
1 . 已知抛物线 ,
, 为直线
为直线 上任意一点,过点
上任意一点,过点 作抛物线
作抛物线 的两条切线
的两条切线 ,
, ,切点分别为
,切点分别为 ,
, .
.
(1)当 的坐标为
的坐标为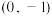 时,求过
时,求过 ,
, ,
, 三点的圆的方程;
三点的圆的方程;
(2)若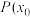 ,
, 是
是 上的任意点,求证:
上的任意点,求证: 点处的切线的斜率为
点处的切线的斜率为 ;
;
(3)证明:以 为直径的圆恒过点
为直径的圆恒过点 .
.
 ,
, 为直线
为直线 上任意一点,过点
上任意一点,过点 作抛物线
作抛物线 的两条切线
的两条切线 ,
, ,切点分别为
,切点分别为 ,
, .
.(1)当
 的坐标为
的坐标为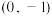 时,求过
时,求过 ,
, ,
, 三点的圆的方程;
三点的圆的方程;(2)若
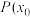 ,
, 是
是 上的任意点,求证:
上的任意点,求证: 点处的切线的斜率为
点处的切线的斜率为 ;
;(3)证明:以
 为直径的圆恒过点
为直径的圆恒过点 .
.
您最近一年使用:0次
名校
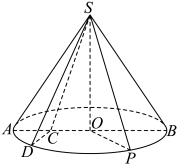
2 . 如图,在圆锥 中,高
中,高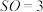 ,底面圆
,底面圆 的直径
的直径 ,
, 是
是 的中点,点
的中点,点 在圆
在圆 上,平面
上,平面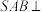 平面
平面 .
. ;
;
(2)若点 是圆
是圆 上动点,求平面
上动点,求平面 与平面
与平面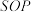 夹角余弦值的取值范围.
夹角余弦值的取值范围.
 中,高
中,高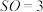 ,底面圆
,底面圆 的直径
的直径 ,
, 是
是 的中点,点
的中点,点 在圆
在圆 上,平面
上,平面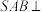 平面
平面 .
.
 ;
;(2)若点
 是圆
是圆 上动点,求平面
上动点,求平面 与平面
与平面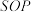 夹角余弦值的取值范围.
夹角余弦值的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 已知在平面直角坐标系xOy中,圆C的圆心在直线l: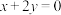 上,圆D与直线l相切,
上,圆D与直线l相切,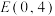 ,且线段OE为圆C与圆D的公共弦.
,且线段OE为圆C与圆D的公共弦.
(1)分别求圆C与圆D的标准方程;
(2)若直线m: 与圆C、圆D分别交于异于原点的两点Q,P,求证:以线段PQ为直径的圆M恒过定点E.
与圆C、圆D分别交于异于原点的两点Q,P,求证:以线段PQ为直径的圆M恒过定点E.
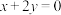 上,圆D与直线l相切,
上,圆D与直线l相切,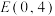 ,且线段OE为圆C与圆D的公共弦.
,且线段OE为圆C与圆D的公共弦.(1)分别求圆C与圆D的标准方程;
(2)若直线m:
 与圆C、圆D分别交于异于原点的两点Q,P,求证:以线段PQ为直径的圆M恒过定点E.
与圆C、圆D分别交于异于原点的两点Q,P,求证:以线段PQ为直径的圆M恒过定点E.
您最近一年使用:0次
2023-10-25更新
|
367次组卷
|
3卷引用:模块二 专题2 解析几何中定值、定点、定直线问题【讲】(高二期中压轴专项)
(已下线)模块二 专题2 解析几何中定值、定点、定直线问题【讲】(高二期中压轴专项)河南省湘豫名校联考2023-2024学年高二上学期10月阶段性考试数学试题广东省广州市广东实验中学越秀学校2023-2024学年高二上学期期中数学试题
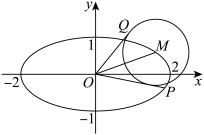
4 . 如图,在平面直角坐标系 中,设点
中,设点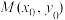 是椭圆C:
是椭圆C: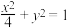 上一点,从原点O向圆
上一点,从原点O向圆 作两条切线,分别与椭圆C交于点
作两条切线,分别与椭圆C交于点 ,直线
,直线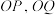 的斜率分别记为
的斜率分别记为 .
.
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若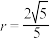 ,求证:
,求证: ;
;
(3)在(2)的情况下,求 的最大值.
的最大值.
 中,设点
中,设点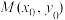 是椭圆C:
是椭圆C: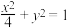 上一点,从原点O向圆
上一点,从原点O向圆 作两条切线,分别与椭圆C交于点
作两条切线,分别与椭圆C交于点 ,直线
,直线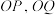 的斜率分别记为
的斜率分别记为 .
.
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若
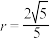 ,求证:
,求证: ;
;(3)在(2)的情况下,求
 的最大值.
的最大值.
您最近一年使用:0次
2023-09-12更新
|
1181次组卷
|
6卷引用:专题06 椭圆的压轴题(6类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)
(已下线)专题06 椭圆的压轴题(6类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)2016届江苏省南京市、盐城市高三第一次模拟考试数学试卷(已下线)专题9.8 直线与圆锥曲线位置关系(练)-江苏版《2020年高考一轮复习讲练测》2017届上海市复旦大学附属中学高三毕业考试数学试题山东省枣庄市滕州市第一中学2022-2023学年高二上学期期中数学试题云南省曲靖市第一中学2024届高三上学期阶段性检测(四)数学试题
名校
解题方法
5 . 已知抛物线C: ,圆M:
,圆M: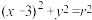 ,圆M上的点到抛物线上的点距离最小值为
,圆M上的点到抛物线上的点距离最小值为 .
.
(1)求圆M的方程;
(2)设P为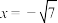 上一点,P的纵坐标不等于
上一点,P的纵坐标不等于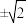 .过点P作圆M的两条切线,分别交抛物线C于两个不同的点
.过点P作圆M的两条切线,分别交抛物线C于两个不同的点 ,
, 和点
和点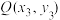 ,
,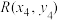 ,求证:
,求证: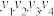 为定值.
为定值.
 ,圆M:
,圆M: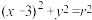 ,圆M上的点到抛物线上的点距离最小值为
,圆M上的点到抛物线上的点距离最小值为 .
.(1)求圆M的方程;
(2)设P为
 上一点,P的纵坐标不等于
上一点,P的纵坐标不等于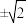 .过点P作圆M的两条切线,分别交抛物线C于两个不同的点
.过点P作圆M的两条切线,分别交抛物线C于两个不同的点 ,
, 和点
和点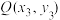 ,
,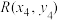 ,求证:
,求证: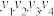 为定值.
为定值.
您最近一年使用:0次
名校
解题方法
6 . 在平面直角坐标系 中,已知圆心在
中,已知圆心在 轴上的圆
轴上的圆 经过点
经过点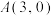 ,且被
,且被 轴截得的弦长为
轴截得的弦长为 .经过坐标原点
.经过坐标原点 的直线
的直线 与圆
与圆 交于
交于 ,
, 两点.
两点.
(1)求圆 的方程;
的方程;
(2)若点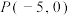 ,直线
,直线 与圆
与圆 的另一个交点为
的另一个交点为 ,直线
,直线 与圆
与圆 的另一个交点为
的另一个交点为 ,分别记直线
,分别记直线 、直线
、直线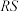 的斜率为
的斜率为 ,
, ,求证:
,求证: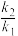 为定值.
为定值.
 中,已知圆心在
中,已知圆心在 轴上的圆
轴上的圆 经过点
经过点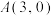 ,且被
,且被 轴截得的弦长为
轴截得的弦长为 .经过坐标原点
.经过坐标原点 的直线
的直线 与圆
与圆 交于
交于 ,
, 两点.
两点.(1)求圆
 的方程;
的方程;(2)若点
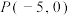 ,直线
,直线 与圆
与圆 的另一个交点为
的另一个交点为 ,直线
,直线 与圆
与圆 的另一个交点为
的另一个交点为 ,分别记直线
,分别记直线 、直线
、直线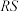 的斜率为
的斜率为 ,
, ,求证:
,求证: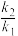 为定值.
为定值.
您最近一年使用:0次
2023-09-14更新
|
1124次组卷
|
5卷引用:专题16 直线与圆的位置关系8种常见考法归类(3)
(已下线)专题16 直线与圆的位置关系8种常见考法归类(3)重庆市南开中学校2023-2024学年高二上学期9月测试数学试题(已下线)专题2.2 直线与圆的位置关系(2个考点十二大题型)(4)(已下线)高二数学上学期第一次月考模拟卷(直线与方程+圆与方程)-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)湖北省宜昌市枝江市第一高级中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
7 . 在平面直角坐标系xOy中,已知圆M过坐标原点O且圆心在曲线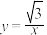 上.
上.
(1)设直线l: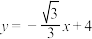 与圆M交于C,D两点,且
与圆M交于C,D两点,且 ,求圆M的方程;
,求圆M的方程;
(2)设直线 与(1)中所求圆M交于E,F两点,点P为直线
与(1)中所求圆M交于E,F两点,点P为直线 上的动点,直线PE,PF与圆M的另一个交点分别为G,H,且G,H在直线EF两侧,求证:直线GH过定点,并求出定点坐标.
上的动点,直线PE,PF与圆M的另一个交点分别为G,H,且G,H在直线EF两侧,求证:直线GH过定点,并求出定点坐标.
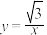 上.
上.(1)设直线l:
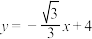 与圆M交于C,D两点,且
与圆M交于C,D两点,且 ,求圆M的方程;
,求圆M的方程;(2)设直线
 与(1)中所求圆M交于E,F两点,点P为直线
与(1)中所求圆M交于E,F两点,点P为直线 上的动点,直线PE,PF与圆M的另一个交点分别为G,H,且G,H在直线EF两侧,求证:直线GH过定点,并求出定点坐标.
上的动点,直线PE,PF与圆M的另一个交点分别为G,H,且G,H在直线EF两侧,求证:直线GH过定点,并求出定点坐标.
您最近一年使用:0次
2023-08-17更新
|
905次组卷
|
7卷引用:第二章 直线与圆的方程(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)
(已下线)第二章 直线与圆的方程(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)重庆市第八中学校2022-2023学年高二上学期第一次月考数学试题四川省凉山州会东县和文中学2022-2023学年高二上学期10月月考数学试题四川省宜宾市叙州区叙州区第一中学校2023-2024学年高二上学期10月月考数学试题安徽省池州市贵池区2023-2024学年高二上学期期中教学质量检测数学试卷(已下线)专题2.2 直线与圆的位置关系(2个考点十二大题型)(2)(已下线)第2章 圆与方程综合能力测试-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
8 . 已知圆C经过两点 ,
,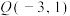 ,且圆心在直线
,且圆心在直线 上,直线l的方程为
上,直线l的方程为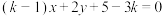 .
.
(1)求圆C的方程;
(2)证明:直线l与圆C恒相交.
 ,
,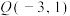 ,且圆心在直线
,且圆心在直线 上,直线l的方程为
上,直线l的方程为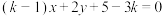 .
.(1)求圆C的方程;
(2)证明:直线l与圆C恒相交.
您最近一年使用:0次
2023-08-03更新
|
1355次组卷
|
5卷引用:第02讲 2.4圆的方程+2.5直线与圆,圆与圆的位置关系(1)
(已下线)第02讲 2.4圆的方程+2.5直线与圆,圆与圆的位置关系(1)人教A版(2019) 选修第一册 第二章 直线和圆的方程 章末达标检测卷人教A版(2019) 选修第一册 数学奇书 第二章 直线和圆的方程 章末整合提升(已下线)2.5.1 直线与圆的位置关系(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)内蒙古自治区赤峰市红山区赤峰第四中学桥北新校2023-2024学年高二上学期期中数学试题
名校
解题方法
9 . 已知双曲线 上任意一点P(异于顶点)与双曲线两顶点连线的斜率之积为
上任意一点P(异于顶点)与双曲线两顶点连线的斜率之积为 ,E在双曲线C上,F为双曲线C的右焦点,
,E在双曲线C上,F为双曲线C的右焦点,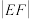 的最小值为
的最小值为 .
.
(1)求双曲线C的标准方程;
(2)设O为坐标原点,直线l为双曲线C的切线,过F作 的垂线,垂足为A,求证:A在定圆上.
的垂线,垂足为A,求证:A在定圆上.
 上任意一点P(异于顶点)与双曲线两顶点连线的斜率之积为
上任意一点P(异于顶点)与双曲线两顶点连线的斜率之积为 ,E在双曲线C上,F为双曲线C的右焦点,
,E在双曲线C上,F为双曲线C的右焦点,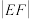 的最小值为
的最小值为 .
.(1)求双曲线C的标准方程;
(2)设O为坐标原点,直线l为双曲线C的切线,过F作
 的垂线,垂足为A,求证:A在定圆上.
的垂线,垂足为A,求证:A在定圆上.
您最近一年使用:0次
名校
10 . 已知圆 过点
过点 ,
,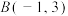 ,且圆心在直线
,且圆心在直线 上.
上.
(1)求圆 的方程;
的方程;
(2)设点 在圆上运动,点
在圆上运动,点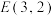 ,记
,记 为过
为过 ,
, 两点的弦的中点,求
两点的弦的中点,求 的轨迹方程;
的轨迹方程;
(3)在(2)的条件下,若直线 与直线
与直线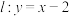 交于点
交于点 ,证明:
,证明: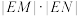 恒为定值.
恒为定值.
 过点
过点 ,
,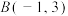 ,且圆心在直线
,且圆心在直线 上.
上.(1)求圆
 的方程;
的方程;(2)设点
 在圆上运动,点
在圆上运动,点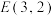 ,记
,记 为过
为过 ,
, 两点的弦的中点,求
两点的弦的中点,求 的轨迹方程;
的轨迹方程;(3)在(2)的条件下,若直线
 与直线
与直线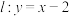 交于点
交于点 ,证明:
,证明: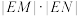 恒为定值.
恒为定值.
您最近一年使用:0次
2023-10-01更新
|
1479次组卷
|
6卷引用:难关必刷03圆的综合问题-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)
(已下线)难关必刷03圆的综合问题-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)专题17 直线与圆的位置关系9种常见考法归类- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)湖北省黄冈市黄州中学(黄冈市外国语学校)2023-2024学年高二实验朝阳班上学期第五次阶段性测试(10月)数学试题广东省东莞市第四高级中学2024-2025学年高二上学期10月期中考试数学试题福建省厦门第一中学2022-2023学年高二上学期10月月考数学试题福建省厦门市湖滨中学2023-2024学年高二上学期期中数学试题



