1 .
已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为− .记M的轨迹为曲线C.
.记M的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(i)证明: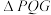 是直角三角形;
是直角三角形;
(ii)求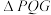 面积的最大值.
面积的最大值.
您最近一年使用:0次
2019-06-09更新
|
36662次组卷
|
63卷引用:山西省晋城市高平一中、阳城一中、高平实验中学2020-2021学年高二上学期期末联考数学(理)试题
山西省晋城市高平一中、阳城一中、高平实验中学2020-2021学年高二上学期期末联考数学(理)试题山西省晋城市(高平一中、阳城一中、高平实验中学)2020-2021学年高二上学期期末数学(理)试题湖南省常德市临澧县第一中学2022-2023学年高二上学期期末数学试题2019年全国统一高考数学试卷(理科)(新课标Ⅱ)(已下线)专题05 平面解析几何——2019年高考真题和模拟题理科数学分项汇编(已下线)专题9.8 直线与圆锥曲线的位置关系(讲)-浙江版《2020年高考一轮复习讲练测》上海市交通大学附属中学2019-2020学年高三上学期9月月考数学试题黑龙江省哈尔滨市尚志市尚志中学2019-2020学年高二上学期第三次月考数学(理)试卷黑龙江省哈尔滨市尚志市尚志中学2019-2020学年高二上学期第三次月考数学(文)试卷(已下线)专题02 化繁为简,轻松驾驭解析几何运算有技巧(第五篇)-2020高考数学压轴题命题区间探究与突破(已下线)专题19 圆锥曲线综合-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)易错点09 解析几何-备战2021年新高考数学一轮复习易错题(已下线)专题08 平面解析几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 综合拔高练人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.1 综合拔高练(已下线)专题29 圆锥曲线的综合问题-十年(2011-2020)高考真题数学分项黑龙江省双鸭山一中2020-2021学年高二(10月分)第一次月考数学(理科)试题(已下线)专题15 直线与椭圆、抛物线的位置关系-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)专题9.9 高考解答题热点题型(一)圆锥曲线中的范围、最值问题-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破安徽省淮北市第一中学2020-2021学年高二上学期期中数学试题(已下线)考点42 曲线与方程-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.7 圆锥曲线综合问题(精讲)-2021年新高考数学一轮复习学与练(已下线)专题9.7 圆锥曲线综合问题(练)-2021年新高考数学一轮复习讲练测(已下线)考点35 椭圆的标准方程及几何性质-备战2021年新高考数学一轮复习考点一遍过(已下线)专题13 解析几何中的范围、最值和探索性问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题17 圆锥曲线中的椭圆问题-2021年高考数学二轮优化提升专题训练(新高考地区专用)【学科网名师堂】(已下线)专题4.5 圆锥曲线-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】 (5月30日)(已下线)押第20题 解析几何-备战2021年高考数学(理)临考题号押题(全国卷1)(已下线)解密18 椭圆(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)预测10 圆锥曲线中的综合性问题-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】(已下线)押第20题 圆锥曲线-备战2021年高考数学(理)临考题号押题(全国卷2)苏教版(2019) 选修第一册 突围者 第3章 章末培优专练(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(讲)(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(练)人教B版(2019) 选修第一册 过关检测 第二章 专项把关练(已下线)专题20 椭圆、抛物线(解答题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)专题13圆锥曲线范围最值问题(练)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(讲)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题40 轨迹方程求解方法-学会解题之高三数学万能解题模板【2022版】(已下线)技巧04 解答题解法与技巧(讲)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题42 盘点圆锥曲线中的面积问题——备战2022年高考数学二轮复习常考点专题突破(已下线)专题4 圆锥曲线的综合应用-学会解题之高三数学321训练体系【2022版】(已下线)押全国卷(理科)第20题 圆锥曲线-备战2022年高考数学(理)临考题号押题(全国卷)(已下线)专题19 圆锥曲线解答题(已下线)考点23圆锥曲线综合应用-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)2023版 湘教版(2019) 选修第一册 过关斩将 第3章 综合拔高练沪教版(2020) 选修第一册 精准辅导 第2章 2.5(1) 求轨迹方程(已下线)专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题(已下线)考向37 圆锥曲线中的范围、最值问题(重点)上海市浦东复旦附中分校2022届高三上学期10月月考数学试题上海市2023届高三二模暨秋考模拟7数学试题全国甲乙卷真题5年分类汇编《解析几何》解答题3.1 椭圆黑龙江省大庆市肇州县第二中学2023届高三下学期开学考试数学试题广东省深圳市红岭中学2023-2024学年高三第五次统一考试数学试题河南省信阳市浉河区信阳高级中学2024届高三上学期1月月考数学试题(已下线)专题2 垂径定理 拓展延伸 练(已下线)7.5 直线和圆锥曲线的综合问题(高考真题素材之十年高考)(已下线)专题24 解析几何解答题(理科)-3专题36平面解析几何解答题(第一部分)(已下线)专题15 利用仿射变换解椭圆、双曲线综合题(一)(高三压轴题)【讲】(已下线)专题15 利用仿射变换解椭圆、双曲线综合题(二)(高三压轴题)【讲】
9-10高一下·黑龙江哈尔滨·期末
名校
解题方法
2 . 设椭圆 过点
过点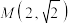 ,
, 两点,O为坐标原点.
两点,O为坐标原点.
(1)求椭圆E的标准方程;
(2)是否存在圆心为原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
 过点
过点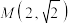 ,
, 两点,O为坐标原点.
两点,O为坐标原点.(1)求椭圆E的标准方程;
(2)是否存在圆心为原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
您最近一年使用:0次
2022-02-28更新
|
1829次组卷
|
16卷引用:2010年哈尔滨市第六中学高一下学期期末考试数学卷
(已下线)2010年哈尔滨市第六中学高一下学期期末考试数学卷天津市静海县第一中学2017-2018学年高二上学期期末终结性检测数学(理)试题(附加题)上海市徐汇区位育中学2015-2016学年高二上学期期末数学试题安徽省合肥市第一中学2021-2022学年高二上学期期末数学试题(已下线)高二上学期期末【压轴60题考点专练】(选修一+选修二)(已下线)2011~2012学年河北省衡水中学高三下学期理科数学试卷2015-2016学年江西省上饶二中高二上学期第三次月考文科数学试卷湖南省长沙市望城区第二中学2019-2020学年高二上学期第二次月考数学试题湖南省邵阳市邵东县第一中学2020-2021学年高二上学期期中数学试题高中数学解题兵法 第八十讲 数学解题、四大环节安徽省亳州市第一中学2021-2022学年高二下学期开年考数学试题四川省泸州市泸州老窖天府中学2020-2021学年高二上学期期中数学(文)试题四川省泸州老窖天府中学2020-2021学年高二上学期期中数学(理)试题天津市十二区县重点学校2022届高三下学期一模考前模拟数学试题(已下线)突破3.1 椭圆(课时训练)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)河南省郑州市一八联合国际学校2023-2024学年高二上学期第三次月考数学试卷
3 . 设椭圆 的左右焦点
的左右焦点 ,
, 分别是双曲线
分别是双曲线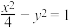 的左右顶点,且椭圆的右顶点到双曲线的渐近线的距离为
的左右顶点,且椭圆的右顶点到双曲线的渐近线的距离为 .
.
(1)求椭圆 的方程;
的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆 恒有两个交点
恒有两个交点 ,且
,且 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
 的左右焦点
的左右焦点 ,
, 分别是双曲线
分别是双曲线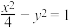 的左右顶点,且椭圆的右顶点到双曲线的渐近线的距离为
的左右顶点,且椭圆的右顶点到双曲线的渐近线的距离为 .
.(1)求椭圆
 的方程;
的方程;(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆
 恒有两个交点
恒有两个交点 ,且
,且 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
您最近一年使用:0次
2022-12-07更新
|
1764次组卷
|
9卷引用:湖北省武汉市江岸区2022-2023学年高二上学期期末数学试题
湖北省武汉市江岸区2022-2023学年高二上学期期末数学试题福建省龙岩第一中学2022-2023学年高二上学期期末质量检测数学模拟试题湖南省岳阳县第一中学、汨罗市第一中学2022-2023学年高二上学期期末考试数学试题(已下线)模块四 专题3 重组综合练(湖北)期末终极研习室(高二人教A版)湖南师范大学附属中学2022-2023学年高三上学期月考(四)数学试题湖北省武汉市华中科技大学附属中学2022-2023学年高二下学期2月月考数学试题(已下线)第09讲 拓展三:圆锥曲线的方程(弦长问题)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第一册)(已下线)重难点突破06 弦长问题及长度和、差、商、积问题(七大题型)-2江西省九江市第七中学2024届高三上学期12月学情诊断数学试题
名校
解题方法
4 . 已知椭圆 的离心率为
的离心率为 ,C上的点到其焦点的最大距离为
,C上的点到其焦点的最大距离为 .
.
(1)求C的方程;
(2)若圆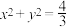 的切线l与C交于点A,B,求
的切线l与C交于点A,B,求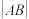 的最大值.
的最大值.
 的离心率为
的离心率为 ,C上的点到其焦点的最大距离为
,C上的点到其焦点的最大距离为 .
.(1)求C的方程;
(2)若圆
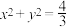 的切线l与C交于点A,B,求
的切线l与C交于点A,B,求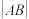 的最大值.
的最大值.
您最近一年使用:0次
2023-03-11更新
|
728次组卷
|
4卷引用:辽宁省农村重点高中协作体2022-2023学年高二上学期期末考试数学试题
辽宁省农村重点高中协作体2022-2023学年高二上学期期末考试数学试题新疆兵团地州学校2022-2023学年高二上学期期末联考数学试题福建省莆田第十中学2022-2023学年高二下学期3月月考数学试题(已下线)第09讲 拓展三:圆锥曲线的方程(弦长问题)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第一册)
5 . 在平面直角坐标系中,椭圆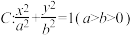 的离心率为
的离心率为 ,焦距为2.
,焦距为2.
(1)求椭圆C的方程;
(2)动直线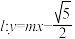 交椭圆于A、B两点,D是椭圆C上一点,直线OD的斜率为
交椭圆于A、B两点,D是椭圆C上一点,直线OD的斜率为 ,且
,且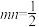 .T是线段OD延长线上一点,且
.T是线段OD延长线上一点,且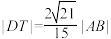 ,
,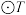 的半径为
的半径为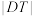 ,OP,OQ是
,OP,OQ是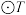 的两条切线,切点分别为P,Q,求
的两条切线,切点分别为P,Q,求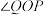 的最大值.
的最大值.
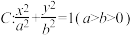 的离心率为
的离心率为 ,焦距为2.
,焦距为2.(1)求椭圆C的方程;
(2)动直线
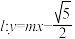 交椭圆于A、B两点,D是椭圆C上一点,直线OD的斜率为
交椭圆于A、B两点,D是椭圆C上一点,直线OD的斜率为 ,且
,且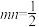 .T是线段OD延长线上一点,且
.T是线段OD延长线上一点,且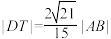 ,
,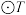 的半径为
的半径为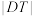 ,OP,OQ是
,OP,OQ是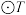 的两条切线,切点分别为P,Q,求
的两条切线,切点分别为P,Q,求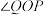 的最大值.
的最大值.
您最近一年使用:0次
2022-10-12更新
|
1194次组卷
|
7卷引用:湖北省恩施州高中教育联盟2022-2023学年高二上学期期末数学试题
6 . 已知椭圆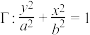 (
( )的离心率为
)的离心率为 ,其上焦点
,其上焦点 与抛物线
与抛物线 的焦点重合.
的焦点重合.
(1)求椭圆 的方程;
的方程;
(2)若过点 的直线交椭圆
的直线交椭圆 于点
于点 ,同时交抛物线
,同时交抛物线 于点
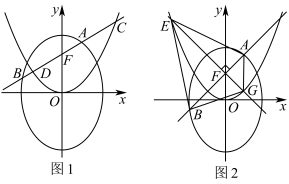
于点 (如图1所示,点
(如图1所示,点 在椭圆与抛物线第一象限交点上方),试比较线段
在椭圆与抛物线第一象限交点上方),试比较线段 与
与 长度的大小,并说明理由;
长度的大小,并说明理由;
(3)若过点 的直线交椭圆
的直线交椭圆 于点
于点 ,过点
,过点 与直线
与直线 垂直的直线
垂直的直线 交抛物线
交抛物线 于点
于点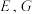 (如图2所示),试求四边形
(如图2所示),试求四边形 面积的最小值.
面积的最小值.
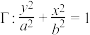 (
( )的离心率为
)的离心率为 ,其上焦点
,其上焦点 与抛物线
与抛物线 的焦点重合.
的焦点重合.
(1)求椭圆
 的方程;
的方程;(2)若过点
 的直线交椭圆
的直线交椭圆 于点
于点 ,同时交抛物线
,同时交抛物线 于点
于点 (如图1所示,点
(如图1所示,点 在椭圆与抛物线第一象限交点上方),试比较线段
在椭圆与抛物线第一象限交点上方),试比较线段 与
与 长度的大小,并说明理由;
长度的大小,并说明理由;(3)若过点
 的直线交椭圆
的直线交椭圆 于点
于点 ,过点
,过点 与直线
与直线 垂直的直线
垂直的直线 交抛物线
交抛物线 于点
于点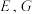 (如图2所示),试求四边形
(如图2所示),试求四边形 面积的最小值.
面积的最小值.
您最近一年使用:0次
名校
解题方法
7 . 1.在平面直角坐标系 中,椭圆
中,椭圆 :
: 的离心率为
的离心率为 ,焦距为2.
,焦距为2.
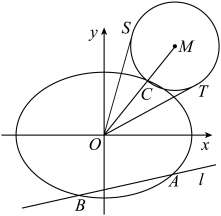
(1)求椭圆 的方程;
的方程;
(2)如图,动直线 :
: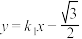 交椭圆
交椭圆 于A,
于A, 两点,
两点, 是椭圆
是椭圆 上一点,直线
上一点,直线 的斜率为
的斜率为 ,且
,且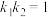 ,
, 是线段
是线段 延长线上一点,且
延长线上一点,且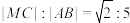 ,
,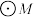 的半径为
的半径为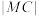 ,
,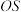 ,
,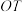 是
是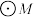 的两条切线,切点分别为S,
的两条切线,切点分别为S, .求
.求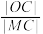 的最小值及
的最小值及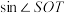 的最大值.
的最大值.
 中,椭圆
中,椭圆 :
: 的离心率为
的离心率为 ,焦距为2.
,焦距为2.
(1)求椭圆
 的方程;
的方程;(2)如图,动直线
 :
: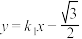 交椭圆
交椭圆 于A,
于A, 两点,
两点, 是椭圆
是椭圆 上一点,直线
上一点,直线 的斜率为
的斜率为 ,且
,且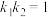 ,
, 是线段
是线段 延长线上一点,且
延长线上一点,且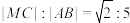 ,
,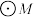 的半径为
的半径为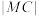 ,
,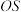 ,
,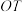 是
是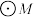 的两条切线,切点分别为S,
的两条切线,切点分别为S, .求
.求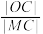 的最小值及
的最小值及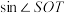 的最大值.
的最大值.
您最近一年使用:0次
2021-11-14更新
|
1568次组卷
|
5卷引用:福建师范大学附属中学2022-2023学年高二上学期期末考试数学试题
名校
解题方法
8 . 已知椭圆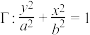 (
( )的离心率为
)的离心率为 ,其上焦点
,其上焦点 与抛物线
与抛物线 的焦点重合.若过点
的焦点重合.若过点 的直线交椭圆
的直线交椭圆 于点
于点 ,过点
,过点 与直线
与直线 垂直的直线
垂直的直线 交抛物线
交抛物线 于点
于点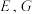 (如图所示),则四边形
(如图所示),则四边形 面积的最小值为
面积的最小值为_________ .
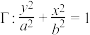 (
( )的离心率为
)的离心率为 ,其上焦点
,其上焦点 与抛物线
与抛物线 的焦点重合.若过点
的焦点重合.若过点 的直线交椭圆
的直线交椭圆 于点
于点 ,过点
,过点 与直线
与直线 垂直的直线
垂直的直线 交抛物线
交抛物线 于点
于点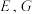 (如图所示),则四边形
(如图所示),则四边形 面积的最小值为
面积的最小值为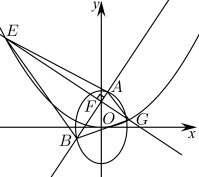
您最近一年使用:0次
2024-01-12更新
|
546次组卷
|
4卷引用:上海市青浦区朱家角中学2023-2024学年高二上学期期末考试数学试题
上海市青浦区朱家角中学2023-2024学年高二上学期期末考试数学试题(已下线)专题04 圆锥曲线(六大题型+优选提升题)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)江西省新余市实验中学2023-2024学年高二下学期开学摸底考试数学试卷(已下线)专题02 圆锥曲线中的求值问题(三大题型)
9 . 已知椭圆 :
: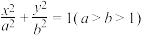 的左、右焦点分别为
的左、右焦点分别为 ,
, ,上顶点为
,上顶点为 ,
, 到直线
到直线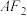 的距离为
的距离为 ,且
,且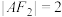 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 的直线m与椭圆
的直线m与椭圆 交于
交于 两点,过
两点,过 且与m垂直的直线n与圆O:
且与m垂直的直线n与圆O: 交于C,D两点,求
交于C,D两点,求 的取值范围.
的取值范围.
 :
: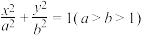 的左、右焦点分别为
的左、右焦点分别为 ,
, ,上顶点为
,上顶点为 ,
, 到直线
到直线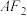 的距离为
的距离为 ,且
,且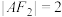 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过
 的直线m与椭圆
的直线m与椭圆 交于
交于 两点,过
两点,过 且与m垂直的直线n与圆O:
且与m垂直的直线n与圆O: 交于C,D两点,求
交于C,D两点,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
10 . 已知点 是圆
是圆 的动点,过
的动点,过 作
作 轴,
轴, 为垂足,且
为垂足,且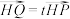 ,
, ,记动点
,记动点 ,
, 的轨迹分别为
的轨迹分别为 ,
, .
.
(1)证明: ,
, 有相同的离心率;
有相同的离心率;
(2)若直线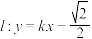 与曲线
与曲线 交于
交于 ,
, ,与曲线
,与曲线 交于
交于 ,
, ,与圆
,与圆 交于
交于 ,
, ,当
,当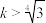 时,试比较
时,试比较 与
与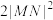 的大小.
的大小.
 是圆
是圆 的动点,过
的动点,过 作
作 轴,
轴, 为垂足,且
为垂足,且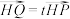 ,
, ,记动点
,记动点 ,
, 的轨迹分别为
的轨迹分别为 ,
, .
.(1)证明:
 ,
, 有相同的离心率;
有相同的离心率;(2)若直线
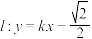 与曲线
与曲线 交于
交于 ,
, ,与曲线
,与曲线 交于
交于 ,
, ,与圆
,与圆 交于
交于 ,
, ,当
,当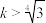 时,试比较
时,试比较 与
与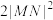 的大小.
的大小.
您最近一年使用:0次
2024-02-28更新
|
435次组卷
|
2卷引用:浙江省金华市2023-2024学年高三上学期2月期末考试数学试题



