名校
1 . 核电站某项具有高辐射危险的工作需要工作人员去完成,每次只派一人,每人只派一次,工作时长不超过15分钟,若某人15分钟内不能完成该工作,则撤出,再派下一人,现有小胡、小邱、小邓三人可派,且他们各自完成工作的概率分别为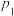 ,
,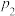 ,
,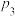 .假设
.假设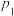 ,
,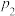 ,
,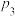 互不相等,且假定三人能否完成工作是相互独立.
互不相等,且假定三人能否完成工作是相互独立.
(1)任务能被完成的概率是否与三个人被派出的先后顺序有关?试说明理由;
(2)若按某指定顺序派出,这三人各自能完成任务的概率依次为 ,
,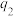 ,
,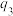 ,其中
,其中 ,
,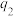 ,
,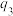 是
是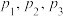 的一个排列.
的一个排列.
①求所需派出人员数目X的分布列和数学期望 ;
;
②假定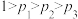 ,为使所需派出的人员数目的数学期望达到最小,应以怎么样的顺序派出?
,为使所需派出的人员数目的数学期望达到最小,应以怎么样的顺序派出?
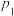 ,
,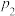 ,
,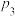 .假设
.假设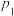 ,
,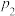 ,
,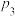 互不相等,且假定三人能否完成工作是相互独立.
互不相等,且假定三人能否完成工作是相互独立.(1)任务能被完成的概率是否与三个人被派出的先后顺序有关?试说明理由;
(2)若按某指定顺序派出,这三人各自能完成任务的概率依次为
 ,
,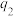 ,
,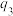 ,其中
,其中 ,
,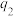 ,
,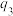 是
是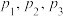 的一个排列.
的一个排列.①求所需派出人员数目X的分布列和数学期望
 ;
;②假定
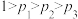 ,为使所需派出的人员数目的数学期望达到最小,应以怎么样的顺序派出?
,为使所需派出的人员数目的数学期望达到最小,应以怎么样的顺序派出?
您最近一年使用:0次
2022-10-25更新
|
1642次组卷
|
5卷引用:重庆市七校2023届高三三诊数学试题
重庆市七校2023届高三三诊数学试题重庆市第八中学校2023届高三上学期高考适应性月考(二)数学试题(已下线)专题42 概率与统计的综合应用-3浙江省杭州市桐庐中学2022-2023学年高三上学期1月期末数学试题(已下线)7.3 离散型随机变量的数字特征(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第三册)
2 . 对于一个古典概型的样本空间 和事件A,B,C,D,其中
和事件A,B,C,D,其中 ,
, ,
, ,
, ,
,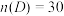 ,
,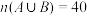 ,
,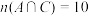 ,
,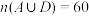 ,则( )
,则( )
 和事件A,B,C,D,其中
和事件A,B,C,D,其中 ,
, ,
, ,
, ,
,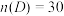 ,
,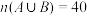 ,
,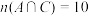 ,
,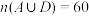 ,则( )
,则( )| A.A与B不互斥 | B.A与D互斥但不对立 |
| C.C与D互斥 | D.A与C相互独立 |
您最近一年使用:0次
2022-05-28更新
|
4255次组卷
|
19卷引用:重庆市缙云教育联盟2023届高三第三次诊断性检测数学试题
重庆市缙云教育联盟2023届高三第三次诊断性检测数学试题安徽省淮北市2023届高三下学期一模数学试题重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题山西省名校2021-2022学年高一下学期5月联考数学试题(已下线)第11练 概率-2022年【暑假分层作业】高一数学(苏教版2019必修第二册)浙江省杭州市萧山区第十一高级中学2022-2023学年高二上学期第一次阶段性考试数学试题江苏省南通市海安市立发中学2022-2023学年高三上学期学情检测(二)数学试题(已下线)模块三 专题6 概率与统计(已下线)专题17计数原理与概率统计(选填题)(已下线)第43讲 事件的相互独立性(2)第十章《概率》单元达标高分突破必刷卷(培优版)-《考点·题型·技巧》(已下线)第十章:概率 重点题型复习(2) --【题型分类归纳】(已下线)第九章 综合测试B(基础卷)(已下线)第12章 概率初步(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020必修第三册)专题14概率(已下线)专题05 统计与概率-【常考压轴题】单元测试A卷——第十章?概率(已下线)专题25 互斥事件和独立事件-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题11 概率归类(1) -期末考点大串讲(苏教版(2019))
名校
解题方法
3 . 如图,一只蚂蚁从正方形 的顶点A出发,每一次行动顺时针或逆时针经过一条边到达另一顶点,其中顺时针的概率为
的顶点A出发,每一次行动顺时针或逆时针经过一条边到达另一顶点,其中顺时针的概率为 ,逆时针的概率为
,逆时针的概率为 ,设蚂蚁经过n步到达B,D两点的概率分别为
,设蚂蚁经过n步到达B,D两点的概率分别为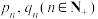 .下列说法正确的有( )
.下列说法正确的有( )

 的顶点A出发,每一次行动顺时针或逆时针经过一条边到达另一顶点,其中顺时针的概率为
的顶点A出发,每一次行动顺时针或逆时针经过一条边到达另一顶点,其中顺时针的概率为 ,逆时针的概率为
,逆时针的概率为 ,设蚂蚁经过n步到达B,D两点的概率分别为
,设蚂蚁经过n步到达B,D两点的概率分别为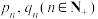 .下列说法正确的有( )
.下列说法正确的有( )
A.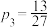 | B.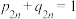 |
C.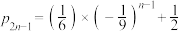 | D.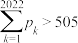 |
您最近一年使用:0次
2022-05-25更新
|
2596次组卷
|
8卷引用:重庆市第八中学校2022届高考全真模拟数学试题
重庆市第八中学校2022届高考全真模拟数学试题(已下线)江苏省盐城市、南京市2022届高三上学期1月第一次模拟考试数学试题变式题11-16黑龙江省哈尔滨德强学校2022-2023学年高三下学期清北班阶段性测试(开学考试)数学试卷(已下线)模块八 专题5 以概率与统计为背景的压轴小题河北省保定市六校联盟2022-2023学年高二下学期4月联考数学试题(已下线)第四篇 概率与统计 专题6 随机游走与马尔科夫过程 微点2 随机游走与马尔科夫过程综合训练(已下线)第5题 马尔科夫链问题 (压轴小题)福建省莆田第二中学、仙游第一中学2023-2024学年高二下学期期中联考数学试题
4 . 2022年2月6日,中国女足在两球落后的情况下,以3比2逆转击败韩国女足,成功夺得亚洲杯冠军,在之前的半决赛中,中国女足通过点球大战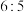 惊险战胜日本女足,其中门将朱钰两度扑出日本队员的点球,表现神勇.
惊险战胜日本女足,其中门将朱钰两度扑出日本队员的点球,表现神勇.
(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑出点球的个数X的分布列和期望;
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑出点球的个数X的分布列和期望;
(2)好成绩的取得离不开平时的努力训练,甲、乙、丙、丁4名女足队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外3人中的1人,接球者接到球后再等可能地随机传向另外3人中的1人,如此不停地传下去,假设传出的球都能接住.记第n次传球之前球在甲脚下的概率为 ,易知
,易知 .
.
①试证明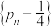 为等比数列;
为等比数列;
②设第n次传球之前球在乙脚下的概率为 ,比较
,比较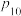 与
与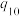 的大小.
的大小.
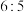 惊险战胜日本女足,其中门将朱钰两度扑出日本队员的点球,表现神勇.
惊险战胜日本女足,其中门将朱钰两度扑出日本队员的点球,表现神勇.(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有
 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑出点球的个数X的分布列和期望;
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑出点球的个数X的分布列和期望;(2)好成绩的取得离不开平时的努力训练,甲、乙、丙、丁4名女足队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外3人中的1人,接球者接到球后再等可能地随机传向另外3人中的1人,如此不停地传下去,假设传出的球都能接住.记第n次传球之前球在甲脚下的概率为
 ,易知
,易知 .
.①试证明
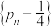 为等比数列;
为等比数列;②设第n次传球之前球在乙脚下的概率为
 ,比较
,比较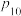 与
与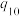 的大小.
的大小.
您最近一年使用:0次
2022-05-12更新
|
6119次组卷
|
21卷引用:重庆市缙云教育联盟2022届高三下学期3月质量检测数学试题
重庆市缙云教育联盟2022届高三下学期3月质量检测数学试题湖北省八市2022届高三下学期3月联考数学试题江苏省淮安市2022届高三下学期5月模拟数学试题江苏省南京市江宁高级中学2022届高三下学期适应性考试数学试题浙江省杭州学军中学西溪校区2021-2022学年高二下学期4月期中数学试题(已下线)三轮冲刺卷04-【赢在高考·黄金20卷】备战2022年高考数学模拟卷(新高考专用)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(6月3日)广东省珠海市第二中学2021-2022学年高二下学期6月月考数学试题(已下线)6.7 均值与方差在生活中的运用(精练)辽宁省锦州市2021-2022学年高二下学期期末考试数学试题(已下线)8.6 分布列与其他知识综合运用(精练)(已下线)高中数学 高二下-4广东省广州市四校2023届高三上学期第二次模拟联考数学试题山东省东营市广饶县第一中学2022-2023学年高三上学期12月月考数学试题山东省威海市第二中学2020-2021学年高二上学期期末数学试题黑龙江省牡丹江市第一高级中学2022-2023学年高三上学期期末数学试题辽宁省沈阳市东北育才双语学校2021-2022学年高二下学期期中数学试题(已下线)第四章 概率与统计(A卷·知识通关练)(3)(已下线)第四篇 概率与统计 专题6 随机游走与马尔科夫过程 微点2 随机游走与马尔科夫过程综合训练(已下线)【一题多变】传球问题 构造数列广东省东莞市东华高级中学、东华松山湖高级中学2022-2023学年高二下学期期末学习效率检测数学试题
名校
解题方法
5 . 规定抽球试验规则如下:盒子中初始装有白球和红球各一个,每次有放回的任取一个,连续取两次,将以上过程记为一轮.如果每一轮取到的两个球都是白球,则记该轮为成功,否则记为失败.在抽取过程中,如果某一轮成功,则停止;否则,在盒子中再放入一个红球,然后接着进行下一轮抽球,如此不断继续下去,直至成功.
(1)某人进行该抽球试验时,最多进行三轮,即使第三轮不成功,也停止抽球,记其进行抽球试验的轮次数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)为验证抽球试验成功的概率不超过 ,有1000名数学爱好者独立的进行该抽球试验,记
,有1000名数学爱好者独立的进行该抽球试验,记 表示成功时抽球试验的轮次数,
表示成功时抽球试验的轮次数, 表示对应的人数,部分统计数据如下:
表示对应的人数,部分统计数据如下:
求 关于
关于 的回归方程
的回归方程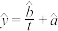 ,并预测成功的总人数(精确到1);
,并预测成功的总人数(精确到1);
(3)证明: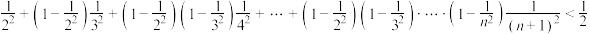 .
.
附:经验回归方程系数: ,
, ;
;
参考数据: ,
,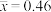 ,
,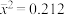 (其中
(其中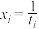 ,
,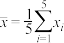 ).
).
(1)某人进行该抽球试验时,最多进行三轮,即使第三轮不成功,也停止抽球,记其进行抽球试验的轮次数为随机变量
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)为验证抽球试验成功的概率不超过
 ,有1000名数学爱好者独立的进行该抽球试验,记
,有1000名数学爱好者独立的进行该抽球试验,记 表示成功时抽球试验的轮次数,
表示成功时抽球试验的轮次数, 表示对应的人数,部分统计数据如下:
表示对应的人数,部分统计数据如下:
| 1 | 2 | 3 | 4 | 5 |
| 232 | 98 | 60 | 40 | 20 |
 关于
关于 的回归方程
的回归方程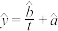 ,并预测成功的总人数(精确到1);
,并预测成功的总人数(精确到1);(3)证明:
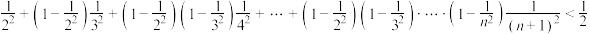 .
.附:经验回归方程系数:
 ,
, ;
;参考数据:
 ,
,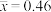 ,
,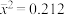 (其中
(其中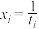 ,
,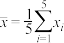 ).
).
您最近一年使用:0次
2022-04-08更新
|
6840次组卷
|
16卷引用:重庆市缙云教育联盟2022届高三第二次诊断性检测数学试题
重庆市缙云教育联盟2022届高三第二次诊断性检测数学试题山东省青岛市2022届三下学期一模数学试题湖北省襄阳市第五中学2022届高三下学期适应性考试(三)数学试题(已下线)秘籍11 统计与概率-备战2022年高考数学抢分秘籍(全国通用)(已下线)第01讲 线性回归分析-【帮课堂】2021-2022学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(6月4日)(已下线)2022年高考考前20天终极冲刺攻略(四)【理科数学】(6月2日)江苏省无锡市天一中学2021-2022学年高二强化班下学期期中数学试题江苏省南京市金陵中学2022届高三学业水平选择性模拟考前最后一卷数学试题(已下线)8.6 分布列与其他知识综合运用(精讲)(已下线)专题17 概率与统计的创新题型(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-1广东省东莞外国语学校2024届高三上学期第一次月考数学试题广东省七校联合体2024届高三上学期开学第一次联考(8月)数学试题专题16回归分析(已下线)专题05 成对数据的统计分析压轴题(1)
6 . 漳州市某路口用停车信号管理,在某日 后的一分钟内有15辆车到达路口,到达的时间如下(以秒作单位):1,4,7,10,14,17,20,22,25,28,30,33,36,38,41.记
后的一分钟内有15辆车到达路口,到达的时间如下(以秒作单位):1,4,7,10,14,17,20,22,25,28,30,33,36,38,41.记 ,2,3,…,15,
,2,3,…,15, 表示第k辆车到达路口的时间,
表示第k辆车到达路口的时间, 表示第k辆车在路口的等待时间,且
表示第k辆车在路口的等待时间,且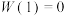 ,
,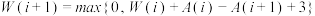 ,
, ,记
,记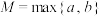 ,M表示a,b中的较大者.
,M表示a,b中的较大者.
(1)从这15辆车中任取2辆,求这两辆车到达路口的时间均在15秒以内的概率;
(2)记这15辆车在路口等待时间的平均值为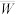 ,现从这15辆车中随机抽取1辆,记
,现从这15辆车中随机抽取1辆,记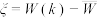 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)通过调查,在该日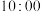 后的一分钟内也有15辆车到达路口,到达的时间如下:1,4,10,14,15,16,17,18,19,21,25,28,30,32,38.现甲驾驶车辆欲在
后的一分钟内也有15辆车到达路口,到达的时间如下:1,4,10,14,15,16,17,18,19,21,25,28,30,32,38.现甲驾驶车辆欲在 后一分钟内或
后一分钟内或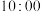 后一分钟内某时刻选择一个通过该路口,试通过比较
后一分钟内某时刻选择一个通过该路口,试通过比较 和
和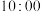 后的一分钟内车辆的平均等待时间,帮甲做出选择.
后的一分钟内车辆的平均等待时间,帮甲做出选择.
 后的一分钟内有15辆车到达路口,到达的时间如下(以秒作单位):1,4,7,10,14,17,20,22,25,28,30,33,36,38,41.记
后的一分钟内有15辆车到达路口,到达的时间如下(以秒作单位):1,4,7,10,14,17,20,22,25,28,30,33,36,38,41.记 ,2,3,…,15,
,2,3,…,15, 表示第k辆车到达路口的时间,
表示第k辆车到达路口的时间, 表示第k辆车在路口的等待时间,且
表示第k辆车在路口的等待时间,且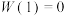 ,
,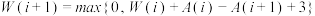 ,
, ,记
,记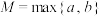 ,M表示a,b中的较大者.
,M表示a,b中的较大者.(1)从这15辆车中任取2辆,求这两辆车到达路口的时间均在15秒以内的概率;
(2)记这15辆车在路口等待时间的平均值为
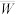 ,现从这15辆车中随机抽取1辆,记
,现从这15辆车中随机抽取1辆,记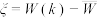 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(3)通过调查,在该日
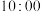 后的一分钟内也有15辆车到达路口,到达的时间如下:1,4,10,14,15,16,17,18,19,21,25,28,30,32,38.现甲驾驶车辆欲在
后的一分钟内也有15辆车到达路口,到达的时间如下:1,4,10,14,15,16,17,18,19,21,25,28,30,32,38.现甲驾驶车辆欲在 后一分钟内或
后一分钟内或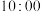 后一分钟内某时刻选择一个通过该路口,试通过比较
后一分钟内某时刻选择一个通过该路口,试通过比较 和
和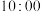 后的一分钟内车辆的平均等待时间,帮甲做出选择.
后的一分钟内车辆的平均等待时间,帮甲做出选择.
您最近一年使用:0次
2022-03-10更新
|
1600次组卷
|
3卷引用:重庆市缙云教育联盟2022届高三下学期第三次诊断性检测数学试题
重庆市缙云教育联盟2022届高三下学期第三次诊断性检测数学试题福建省漳州市2022届高三毕业班第二次教学质量检测数学试题(已下线)专题25 随机变量及其分布- 2022届高考数学一模试题分类汇编(新高考卷)
名校
解题方法
7 . 某5G传输设备由奇数根相同的光导纤维并联组成,每根光导纤维能正常传输信号的概率均为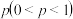 ,且每根光导纤维能否正常传输信号相互独立.已知该设备中有超过一半的光导纤维能正常传输信号,这个5G传输设备才可以正常工作.记
,且每根光导纤维能否正常传输信号相互独立.已知该设备中有超过一半的光导纤维能正常传输信号,这个5G传输设备才可以正常工作.记 根光导纤维组成的这种5G传输设备可以正常工作的概率为
根光导纤维组成的这种5G传输设备可以正常工作的概率为 .
.
(1)用p表示 ;
;
(2)当 时,证明:
时,证明: ;
;
(3)为提高这个5G传输设备正常工作的概率,在这个传输设备上再并联两根相同规格的光导纤维,且新增光导纤维后的5G传输设备有超过一半的光导纤维能正常传输信号才可以正常工作.确定 的取值范围,使新增两根光导纤维可以提高这个5G传输设备正常工作的概率.
的取值范围,使新增两根光导纤维可以提高这个5G传输设备正常工作的概率.
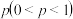 ,且每根光导纤维能否正常传输信号相互独立.已知该设备中有超过一半的光导纤维能正常传输信号,这个5G传输设备才可以正常工作.记
,且每根光导纤维能否正常传输信号相互独立.已知该设备中有超过一半的光导纤维能正常传输信号,这个5G传输设备才可以正常工作.记 根光导纤维组成的这种5G传输设备可以正常工作的概率为
根光导纤维组成的这种5G传输设备可以正常工作的概率为 .
.(1)用p表示
 ;
;(2)当
 时,证明:
时,证明: ;
;(3)为提高这个5G传输设备正常工作的概率,在这个传输设备上再并联两根相同规格的光导纤维,且新增光导纤维后的5G传输设备有超过一半的光导纤维能正常传输信号才可以正常工作.确定
 的取值范围,使新增两根光导纤维可以提高这个5G传输设备正常工作的概率.
的取值范围,使新增两根光导纤维可以提高这个5G传输设备正常工作的概率.
您最近一年使用:0次
名校
解题方法
8 . “博弈”原指下棋,出自我国《论语·阳货》篇,现在多指一种决策行为,即一些个人、团队或组织,在一定规则约束下,同时或先后,一次或多次,在各自允许选择的策略下进行选择和实施,并从中各自取得相应结果或收益的过程.生活中有很多游戏都蕴含着博弈,比如现在有两个人玩“亮”硬币的游戏,甲、乙约定若同时亮出正面,则甲付给乙3元,若同时亮出反面,则甲付给乙1元,若亮出结果是一正一反,则乙付给甲2元.
(1)若两人各自随机“亮”出正反面,求乙收益的期望.
(2)因为各自“亮”出正反面,而不是抛出正反面,所以可以控制“亮”出正面或反面的频率(假设进行多次游戏,频率可以代替概率),因此双方就面临竞争策略的博弈.甲、乙可以根据对手出正面的概率调整自己出正面的概率,进而增加自己赢得收益的期望,以收益的期望为决策依据,甲、乙各自应该如何选择“亮”出正面的概率,才能让结果对自己最有利?并分析游戏规则是否公平.
(1)若两人各自随机“亮”出正反面,求乙收益的期望.
(2)因为各自“亮”出正反面,而不是抛出正反面,所以可以控制“亮”出正面或反面的频率(假设进行多次游戏,频率可以代替概率),因此双方就面临竞争策略的博弈.甲、乙可以根据对手出正面的概率调整自己出正面的概率,进而增加自己赢得收益的期望,以收益的期望为决策依据,甲、乙各自应该如何选择“亮”出正面的概率,才能让结果对自己最有利?并分析游戏规则是否公平.
您最近一年使用:0次
2021-04-08更新
|
2193次组卷
|
5卷引用:重庆市永川北山中学校2022届高三高考冲刺3数学试题
重庆市永川北山中学校2022届高三高考冲刺3数学试题湖南省长沙市一中2021届高三下学期一模数学试题安徽省示范高中皖北协作区2021届高三下学期第23届联考数学(理)试题湖南省长郡、雅礼、一中、附中联合编审名校卷(全国卷)2021届高三月考数学理科试题(九)(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练
名校
9 . 第13届女排世界杯于2019年9月14日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球MIKSA-V200W ,已知这种球的质量指标ξ (单位:g )服从正态分布N (270,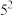 ).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
(1)如果比赛准备了1000个排球,估计质量指标在(260,265]内的排球个数(计算结果取整数).
(2)第10轮比赛中,记中国队3:1取胜的概率为 .
.
(i)求出f(p)的最大值点 ;
;
(ii)若以 作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
参考数据:ζ ~N(u, ),则p(μ-σ<X<μ+σ)≈0.6826,p(μ-2σ<X <μ+2σ)≈0.9544.
),则p(μ-σ<X<μ+σ)≈0.6826,p(μ-2σ<X <μ+2σ)≈0.9544.
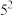 ).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1). (1)如果比赛准备了1000个排球,估计质量指标在(260,265]内的排球个数(计算结果取整数).
(2)第10轮比赛中,记中国队3:1取胜的概率为
 .
.(i)求出f(p)的最大值点
 ;
;(ii)若以
 作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.参考数据:ζ ~N(u,
 ),则p(μ-σ<X<μ+σ)≈0.6826,p(μ-2σ<X <μ+2σ)≈0.9544.
),则p(μ-σ<X<μ+σ)≈0.6826,p(μ-2σ<X <μ+2σ)≈0.9544.
您最近一年使用:0次
2020-11-21更新
|
5912次组卷
|
19卷引用:重庆市第一中2021届高三高考数学押题卷试题(四)
重庆市第一中2021届高三高考数学押题卷试题(四)八省市2021届高三新高考统一适应性考试江苏省无锡市天一中学考前热身模拟数学试题(二)湖北省襄阳市第四中学2021届高三下学期一模数学试题湖北省黄石市有色第一中学2022届高三下学期5月适应性考试数学试题江苏省南京师大附中2020-2021学年高三上学期期中数学试题(已下线)第十一单元 概率与统计 (A卷 基础过关检测)-2021年高考数学(理)一轮复习单元滚动双测卷(已下线)7.5 正态分布(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)必刷卷01-2021年高考数学(理)考前信息必刷卷(新课标卷)(已下线)专题12 概率与统计的综合应用-备战2021年高考数学二轮复习题型专练(新高考专用)广东省深圳市盐田区深圳外国语学校2021届高三上学期1月月考数学试题广东省广州市执信中学2021届高三上学期第四次月考数学试题(已下线)模块检测(提升卷)-2020-2021学年高二数学新教材单元双测卷(人教A版2019选择性必修第三册)(已下线)第49讲 两点分布、超几何分布、二项分布、正态分布-2022年新高考数学二轮专题突破精练(已下线)专题46 随机变量及其分布-学会解题之高三数学万能解题模板【2022版】(已下线)专题10-2 概率统计(解答题)-3(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-3辽宁省沈阳市第一二〇中学2024届高三上学期第五次质量监测数学试题广东省肇庆市肇庆中学2021-2022学年高二下学期第三次学段考试数学试题专题15离散型随机变量的分布列
名校
解题方法
10 . 2019年末,武汉出现新型冠状病毒肺炎(COVID-19)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大,武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为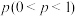 且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为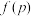 ,当
,当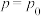 时,
时,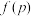 最大,则
最大,则 ()
()
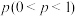 且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为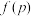 ,当
,当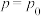 时,
时,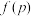 最大,则
最大,则 ()
()A.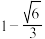 | B. | C. | D.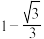 |
您最近一年使用:0次
2020-10-21更新
|
3939次组卷
|
28卷引用:2020届重庆市名校联盟高三二诊数学(理)试题
2020届重庆市名校联盟高三二诊数学(理)试题2020届重庆市名校联盟高三二诊数学(文)试题2020届河北省沧州市高三一模数学(理)试题吉林省吉林市2020届高三第四次调研测试数学(理)试题八省市2021届高三新高考统一适应性考试江苏省无锡市天一中学考前热身模拟数学试题(二)(已下线)冲刺卷06-决战2020年高考数学冲刺卷(山东专版)(已下线)第四篇数学文化03-2020年高考数学选填题专项测试(文理通用)福建省厦门市海沧中学2019-2020学年高三四月强化检测(理科)数学试题吉林省白城市第一中学2019-2020学年高二下学期期末考试数学(理)试题湖南省长沙市雅礼中学2020-2021学年高三上学期月考(二)数学试题四川省成都七中2020-2021学年高三上学期半期考试理科数学试题(已下线)第47练 随机变量及其分布-2021年高考数学(理)一轮复习小题必刷(已下线)黄金卷18-【赢在高考·黄金20卷】备战2021高考数学全真模拟卷(新高考专用)(已下线)黄金卷11-【赢在高考·黄金20卷】备战2021高考数学全真模拟卷(新高考专用)(已下线)4.1.2、4.1.3 乘法公式与全概率公式、独立性与条件概率的关系-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)(已下线)专题18 随机变量及其分布(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)专题19 随机变量及其分布(客观题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题7.6第七章《随机变量及其分布列》综合测试卷(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)专题4.6《随机变量》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)广东省汕头市澄海中学2020-2021学年高二下学期期中数学试题甘肃省静宁县第一中学2020-2021学年高二下学期第二次月考数学(理)(实验班)试题江苏省南京市中华中学2020-2021学年高二下学期期中数学试题(已下线)解密19 随机变量及分布列(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(新高考专用)(已下线)专题21 排列组合与概率必刷小题100题-【千题百练】2022年新高考数学高频考点+题型专项千题百练(新高考适用)(已下线)三轮冲刺卷02-【赢在高考·黄金20卷】备战2022年高考数学模拟卷(新高考专用)(已下线)期中测试卷-2021-2022学年高二数学课后培优练(人教A版2019选择性必修第三册)(已下线)高二数学下学期期中精选50题(压轴版)2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)第九章 重难专攻(十二)概率中的综合题 B素养养成卷 一轮点点通



