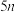解题方法
1 . 某单位有10000名职工,想通过验血的方法筛查出某种细菌感染性疾病.抽样化验显示,当前携带该细菌的人约占0.9%,若逐个化验需化验10000次.统计专家提出了一种化验方法:随机按n人一组进行分组,将各组n个人的血液混合在一起化验,若混合血样呈阴性,则这n个人的血样全部阴性;若混合血样呈阳性,则说明其中至少有一人的血样呈阳性,就需对每个人再分别化验一次.
(1)若每人单独化验一次花费10元,n个人混合化验一次花费 元.问n为何值时,化验费用的数学期望最小?(注:当
元.问n为何值时,化验费用的数学期望最小?(注:当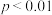 时,
时,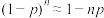 )
)
(2)该疾病主要是通过人与人之间进行传播,感染人群年龄大多数是40岁以上.细菌进入人体后有潜伏期.潜伏期是指病原体侵入人体至最早出现临床症状的这段时间.潜伏期越长,感染给他人的可能性越高.现对已发现的90个病例的潜伏期(单位:天)进行调查,统计发现潜伏期的平均数为7.2,方差为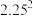 .如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
.如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
①是否有95%的把握认为“长期潜伏”与年龄有关?
②假设潜伏期X服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数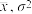 近似为样本方差
近似为样本方差 .为防止该疾病的传播,现要求感染者的密接者居家观察14天,请用概率的知识解释其合理性.
.为防止该疾病的传播,现要求感染者的密接者居家观察14天,请用概率的知识解释其合理性.
附: ,
,
若 ,则
,则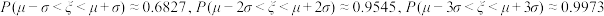 .
.
(1)若每人单独化验一次花费10元,n个人混合化验一次花费
 元.问n为何值时,化验费用的数学期望最小?(注:当
元.问n为何值时,化验费用的数学期望最小?(注:当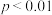 时,
时,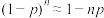 )
)(2)该疾病主要是通过人与人之间进行传播,感染人群年龄大多数是40岁以上.细菌进入人体后有潜伏期.潜伏期是指病原体侵入人体至最早出现临床症状的这段时间.潜伏期越长,感染给他人的可能性越高.现对已发现的90个病例的潜伏期(单位:天)进行调查,统计发现潜伏期的平均数为7.2,方差为
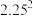 .如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
.如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:| 年龄/人数 | 长期潜伏 | 非长期潜伏 |
| 40岁以上 | 15 | 50 |
| 40岁及40岁以下 | 10 | 15 |
②假设潜伏期X服从正态分布
 ,其中
,其中 近似为样本平均数
近似为样本平均数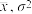 近似为样本方差
近似为样本方差 .为防止该疾病的传播,现要求感染者的密接者居家观察14天,请用概率的知识解释其合理性.
.为防止该疾病的传播,现要求感染者的密接者居家观察14天,请用概率的知识解释其合理性.附:
 ,
, | 0.1 | 0.05 | 0.010 |
 | 2.706 | 3.841 | 6.635 |
 ,则
,则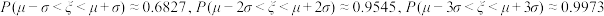 .
.
您最近一年使用:0次
2024-05-05更新
|
554次组卷
|
3卷引用:2024年新高考Ⅰ卷浙大优学靶向精准模拟数学试题(一)
2 . 电信诈骗是指通过电话、网络和短信方式,编造虚假信息,设置骗局,对受害人实施远程诈骗的犯罪行为.随着 时代的全面来临,借助手机、网银等实施的非接触式电信诈骗迅速发展蔓延,不法分子甚至将“魔爪”伸向了学生.为了调查同学们对“反诈”知识的了解情况,某校进行了一次抽样调查.若被调查的男女生人数均为
时代的全面来临,借助手机、网银等实施的非接触式电信诈骗迅速发展蔓延,不法分子甚至将“魔爪”伸向了学生.为了调查同学们对“反诈”知识的了解情况,某校进行了一次抽样调查.若被调查的男女生人数均为 ,统计得到以下列联表.经过计算,依据小概率值
,统计得到以下列联表.经过计算,依据小概率值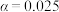 的独立性检验,认为该校学生对“反诈”知识的了解与性别有关,但依据小概率值
的独立性检验,认为该校学生对“反诈”知识的了解与性别有关,但依据小概率值 的独立性检验,认为该校学生对“反诈”知识的了解与性别无关.
的独立性检验,认为该校学生对“反诈”知识的了解与性别无关.
(1)求n的值;
(2)将频率视为概率,用样本估计总体,从全校男生中随机抽取5人,记其中对“反诈”知识了解的人数为X,求X的分布列及数学期望.
(3)为了增强同学们的防范意识,该校举办了主题为“防电信诈骗,做反诈达人”的知识竞赛.已知全校参加本次竞赛的学生分数 近似服从正态分布
近似服从正态分布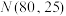 ,若某同学成绩满足
,若某同学成绩满足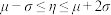 ,则该同学被评为“反诈标兵”;若
,则该同学被评为“反诈标兵”;若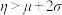 ,则该同学被评为“反诈达人”.
,则该同学被评为“反诈达人”.
(i)试判断分数为88分的同学能否被评为“反诈标兵”;
(ii)若全校共有50名同学被评为“反诈达人”,试估计参与本次知识竞赛的学生人数.(四舍五入后取整)
附: ,其中
,其中 .
.
若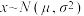 ,则
,则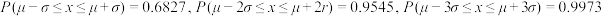 .
.
 时代的全面来临,借助手机、网银等实施的非接触式电信诈骗迅速发展蔓延,不法分子甚至将“魔爪”伸向了学生.为了调查同学们对“反诈”知识的了解情况,某校进行了一次抽样调查.若被调查的男女生人数均为
时代的全面来临,借助手机、网银等实施的非接触式电信诈骗迅速发展蔓延,不法分子甚至将“魔爪”伸向了学生.为了调查同学们对“反诈”知识的了解情况,某校进行了一次抽样调查.若被调查的男女生人数均为 ,统计得到以下列联表.经过计算,依据小概率值
,统计得到以下列联表.经过计算,依据小概率值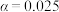 的独立性检验,认为该校学生对“反诈”知识的了解与性别有关,但依据小概率值
的独立性检验,认为该校学生对“反诈”知识的了解与性别有关,但依据小概率值 的独立性检验,认为该校学生对“反诈”知识的了解与性别无关.
的独立性检验,认为该校学生对“反诈”知识的了解与性别无关.性别 | 不了解 | 了解 | 合计 |
女生 |
| ||
男生 |
| ||
合计 |
(2)将频率视为概率,用样本估计总体,从全校男生中随机抽取5人,记其中对“反诈”知识了解的人数为X,求X的分布列及数学期望.
(3)为了增强同学们的防范意识,该校举办了主题为“防电信诈骗,做反诈达人”的知识竞赛.已知全校参加本次竞赛的学生分数
 近似服从正态分布
近似服从正态分布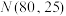 ,若某同学成绩满足
,若某同学成绩满足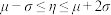 ,则该同学被评为“反诈标兵”;若
,则该同学被评为“反诈标兵”;若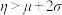 ,则该同学被评为“反诈达人”.
,则该同学被评为“反诈达人”.(i)试判断分数为88分的同学能否被评为“反诈标兵”;
(ii)若全校共有50名同学被评为“反诈达人”,试估计参与本次知识竞赛的学生人数.(四舍五入后取整)
附:
 ,其中
,其中 .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
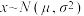 ,则
,则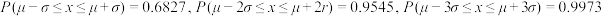 .
.
您最近一年使用:0次
2024-05-05更新
|
1799次组卷
|
5卷引用:2024年新高考Ⅰ卷浙大优学靶向精准模拟数学试题(七)
2024年新高考Ⅰ卷浙大优学靶向精准模拟数学试题(七)(已下线)9.2 成对数据的分析(高考真题素材之十年高考)河北省保定市定州中学2023-2024学年高二下学期五月半月考数学试题广西南宁市第二十六中学2023-2024学年高二下学期5月月考数学试题(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)
名校
解题方法
3 . 下列结论中正确的有( )
A.若随机变量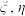 满足 满足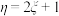 ,则 ,则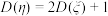 |
B.若随机变量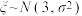 ,且 ,且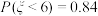 ,则 ,则 |
C.若线性相关系数 越接近1,则两个变量的线性相关性越强 越接近1,则两个变量的线性相关性越强 |
| D.数据40,27,32,30,38,54,31,50的第50百分位数为32 |
您最近一年使用:0次
2024-05-05更新
|
1885次组卷
|
4卷引用:2024年新高考Ⅰ卷浙大优学靶向精准模拟数学试题(六)
2024年新高考Ⅰ卷浙大优学靶向精准模拟数学试题(六)湖南省长沙市第一中学2024届高考适应性演练(三)数学试题(已下线)9.2 成对数据的分析(高考真题素材之十年高考)湖南省岳阳市第一中学2024届高三下学期高考适应性考试数学试题
2024·全国·模拟预测
解题方法
4 . 设随机变量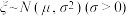 ,则( )
,则( )
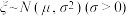 ,则( )
,则( )A.正态曲线关于 对称 对称 |
B.正态曲线随着 的变化而上下波动 的变化而上下波动 |
C.设随机变量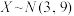 ,则 ,则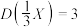 |
D.正态曲线与 轴之间的面积为1 轴之间的面积为1 |
您最近一年使用:0次
2024·全国·模拟预测
名校
解题方法
5 . 下列说法正确的是( )
| A.小明统计了近5次的数学考试成绩,分别是90,120,108,123,116,则这组数据的第60百分位数是116 |
B.一组数据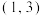 , ,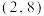 , , , , , , 的经验回归方程为 的经验回归方程为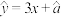 ,则当 ,则当 时,残差为 时,残差为 |
C.一组数据 , , , , , , 的均值为 的均值为 ,标准差为s,则数据 ,标准差为s,则数据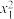 , , ,…, ,…,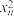 的均值为 的均值为 |
D.设随机变量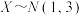 ,且 ,且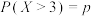 ,则 ,则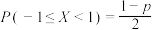 |
您最近一年使用:0次
2024高三·全国·专题练习
6 . 亚运聚欢潮,璀璨共此时,2023年9月第19届亚洲运动会在杭州举办,来自亚洲45个国家和地区的1万多名运动员在这里团结交流、收获友谊,奋勇拼搏、超越自我,共同创造了亚洲体育新的辉煌和荣光,赢得了亚奥理事会大家庭和国际社会的广泛好评.亚运会圆满结束后,杭州某学校组织学生参加与本届亚运会有关的知识竞赛,为了解该校学生对本届亚运会有关赛事知识的掌握情况,采用随机抽样的方法抽取了600名学生进行调查,成绩全部分布在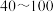 分之间,根据调查结果绘制的学生成绩的频率分布直方图如图所示.
分之间,根据调查结果绘制的学生成绩的频率分布直方图如图所示. 的值.
的值.
(2)估计这600名学生成绩的中位数.
(3)由频率分布直方图可以认为,这次竞赛成绩 近似服从正态分布
近似服从正态分布 ,其中
,其中 为样本平均数(同一组数据用该组数据的区间中点值作代表),
为样本平均数(同一组数据用该组数据的区间中点值作代表),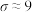 ,试用正态分布知识解决下列问题:
,试用正态分布知识解决下列问题:
①若这次竞赛共有2.8万名学生参加,试估计竞赛成绩超过86.8分的人数(结果精确到个位);②现从所有参赛的学生中随机抽取10人进行座谈,设其中竞赛成绩超过77.8分的人数为 ,求随机变量
,求随机变量 的期望.
的期望.
附:若随机变量 服从正态分布
服从正态分布 ,则
,则 ,
,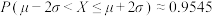 ,
, .
.
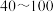 分之间,根据调查结果绘制的学生成绩的频率分布直方图如图所示.
分之间,根据调查结果绘制的学生成绩的频率分布直方图如图所示.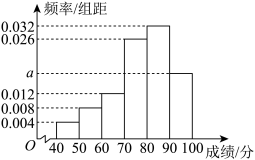
 的值.
的值.(2)估计这600名学生成绩的中位数.
(3)由频率分布直方图可以认为,这次竞赛成绩
 近似服从正态分布
近似服从正态分布 ,其中
,其中 为样本平均数(同一组数据用该组数据的区间中点值作代表),
为样本平均数(同一组数据用该组数据的区间中点值作代表),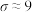 ,试用正态分布知识解决下列问题:
,试用正态分布知识解决下列问题:①若这次竞赛共有2.8万名学生参加,试估计竞赛成绩超过86.8分的人数(结果精确到个位);②现从所有参赛的学生中随机抽取10人进行座谈,设其中竞赛成绩超过77.8分的人数为
 ,求随机变量
,求随机变量 的期望.
的期望.附:若随机变量
 服从正态分布
服从正态分布 ,则
,则 ,
,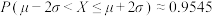 ,
, .
.
您最近一年使用:0次
2024-04-08更新
|
1104次组卷
|
5卷引用:2024年全国高考名校名师联席命制数学押题卷(六)
(已下线)2024年全国高考名校名师联席命制数学押题卷(六)宁夏银川市唐徕中学2024届高三下学期适应性考试数学(理)试题(已下线)2024年全国高考名校名师联席命制数学(理)押题卷(五)(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)宁夏银川一中、云南省昆明一中2024届高三下学期5月联合考试二模理科数学试卷
名校
解题方法
7 . 下列说法正确的是( )
A.若随机变量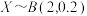 ,则 ,则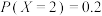 |
B.若经验回归方程 中的 中的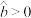 ,则变量 ,则变量 与 与 正相关 正相关 |
C.若随机变量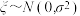 ,且 ,且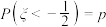 ,则 ,则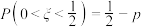 |
D.若事件 与 与 为互斥事件,则 为互斥事件,则 的对立事件与 的对立事件与 的对立事件一定互斥 的对立事件一定互斥 |
您最近一年使用:0次
2024-03-06更新
|
1492次组卷
|
6卷引用:第四套 新高考新结构全真模拟4(艺体生)
名校
解题方法
8 . 正态分布与指数分布均是用于描述连续型随机变量的概率分布.对于一个给定的连续型随机变量 ,定义其累积分布函数为
,定义其累积分布函数为 .已知某系统由一个电源和并联的
.已知某系统由一个电源和并联的 ,
,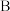 ,
,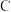 三个元件组成,在电源电压正常的情况下,至少一个元件正常工作才可保证系统正常运行,电源及各元件之间工作相互独立.
三个元件组成,在电源电压正常的情况下,至少一个元件正常工作才可保证系统正常运行,电源及各元件之间工作相互独立.
(1)已知电源电压 (单位:
(单位: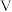 )服从正态分布
)服从正态分布 ,且
,且 的累积分布函数为
的累积分布函数为 ,求
,求 ;
;
(2)在数理统计中,指数分布常用于描述事件发生的时间间隔或等待时间.已知随机变量 (单位:天)表示某高稳定性元件的使用寿命,且服从指数分布,其累积分布函数为
(单位:天)表示某高稳定性元件的使用寿命,且服从指数分布,其累积分布函数为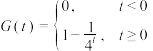 .
.
(ⅰ)设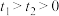 ,证明:
,证明: ;
;
(ⅱ)若第 天元件
天元件 发生故障,求第
发生故障,求第 天系统正常运行的概率.
天系统正常运行的概率.
附:若随机变量 服从正态分布
服从正态分布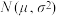 ,则
,则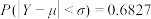 ,
, ,
, .
.
 ,定义其累积分布函数为
,定义其累积分布函数为 .已知某系统由一个电源和并联的
.已知某系统由一个电源和并联的 ,
,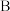 ,
,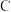 三个元件组成,在电源电压正常的情况下,至少一个元件正常工作才可保证系统正常运行,电源及各元件之间工作相互独立.
三个元件组成,在电源电压正常的情况下,至少一个元件正常工作才可保证系统正常运行,电源及各元件之间工作相互独立.(1)已知电源电压
 (单位:
(单位: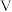 )服从正态分布
)服从正态分布 ,且
,且 的累积分布函数为
的累积分布函数为 ,求
,求 ;
;(2)在数理统计中,指数分布常用于描述事件发生的时间间隔或等待时间.已知随机变量
 (单位:天)表示某高稳定性元件的使用寿命,且服从指数分布,其累积分布函数为
(单位:天)表示某高稳定性元件的使用寿命,且服从指数分布,其累积分布函数为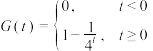 .
.(ⅰ)设
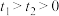 ,证明:
,证明: ;
;(ⅱ)若第
 天元件
天元件 发生故障,求第
发生故障,求第 天系统正常运行的概率.
天系统正常运行的概率.附:若随机变量
 服从正态分布
服从正态分布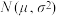 ,则
,则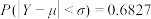 ,
, ,
, .
.
您最近一年使用:0次
名校
9 . 某市为提升中学生的环境保护意识,举办了一次“环境保护知识竞赛”,分预赛和复赛两个环节,预赛成绩排名前三百名的学生参加复赛.已知共有12000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到频率分布直方图如图:
(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布 ,其中
,其中 可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且
可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且 ,已知小明的预赛成绩为91分,利用该正态分布,估计小明是否有资格参加复赛?
,已知小明的预赛成绩为91分,利用该正态分布,估计小明是否有资格参加复赛?
附:若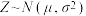 ,则
,则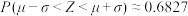 ,
,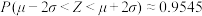 ,
,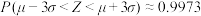 ;
; .
.

(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布
 ,其中
,其中 可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且
可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且 ,已知小明的预赛成绩为91分,利用该正态分布,估计小明是否有资格参加复赛?
,已知小明的预赛成绩为91分,利用该正态分布,估计小明是否有资格参加复赛?附:若
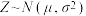 ,则
,则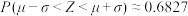 ,
,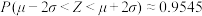 ,
,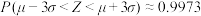 ;
; .
.
您最近一年使用:0次
2024-02-17更新
|
2425次组卷
|
10卷引用:陕西省西安市2024年高三第一次质量检测理科数学试题
陕西省西安市2024年高三第一次质量检测理科数学试题(已下线)第四套 最新模拟重组卷(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第七章 随机变量及其分布(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)广东省2024届高三新改革数学适应性训练六(九省联考题型)(已下线)专题8-2分布列综合归类-1(已下线)7.5 正态分布——课后作业(基础版)陕西省西安高新第一中学2025届高三上学期开学考试数学试题四川省绵竹中学2024-2025学年高三上学期开学考试数学试题江西省宜春市丰城中学2025届高三上学期开学考试数学试题
名校
10 . 面试是求职者进入职场的一个重要关口,也是机构招聘员工的重要环节.某科技企业招聘员工,首先要进行笔试,笔试达标者进入面试,面试环节要求应聘者回答3个问题,第一题考查对公司的了解,答对得2分,答错不得分,第二题和第三题均考查专业知识,每道题答对得4分,答错不得分.
(1)若一共有100人应聘,他们的笔试得分X服从正态分布 ,规定
,规定 为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);
为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);
(2)某进入面试的应聘者第一题答对的概率为 ,后两题答对的概率均为
,后两题答对的概率均为 ,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.
,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.
附:若 (
( ),则
),则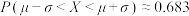 ,
,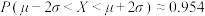 ,
,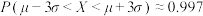 .
.
(1)若一共有100人应聘,他们的笔试得分X服从正态分布
 ,规定
,规定 为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);
为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);(2)某进入面试的应聘者第一题答对的概率为
 ,后两题答对的概率均为
,后两题答对的概率均为 ,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.
,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.附:若
 (
( ),则
),则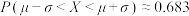 ,
,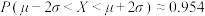 ,
,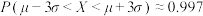 .
.
您最近一年使用:0次
2024-02-14更新
|
3524次组卷
|
13卷引用:2024年普通高等学校招生全国统一考试数学冲刺卷一(九省联考题型)
2024年普通高等学校招生全国统一考试数学冲刺卷一(九省联考题型)河南省信阳市新县高级中学2024届高三下学期3月适应性考试数学试题湖南省长沙市长郡中学2024届高三下学期模拟(一)数学试卷江西省南昌市八一中学2024届高三下学期三模测试数学试题(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题8-2分布列综合归类-1宁夏银川市六盘山高级中学2023-2024学年高二下学期5月月考数学试题江西省九师联盟2024届高三上学期1月质量检测试数学试题江西省宜春市上高二中2024届高三上学期期末数学试题(已下线)黄金卷02(2024新题型)湖南省衡阳市衡阳县第二中学2023-2024学年高二下学期期中达标数学测评卷广东省江门市新会第一中学2023-2024学年高二下学期期末考试数学试题福建省安溪第八中学2024-2025学年高三上学期8月份质量检测数学试题