名校
解题方法
1 . 在2021年6月某区的高二期末质量检测考试中,学生的数学成绩服从正态分布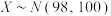 .已知参加本次考试的学生约有9450人,如果某学生在这次考试中数学成绩为108分,那么他的数学成绩大约排在该区的名次是
.已知参加本次考试的学生约有9450人,如果某学生在这次考试中数学成绩为108分,那么他的数学成绩大约排在该区的名次是______ .附:若 ,则
,则 ,
,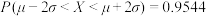 .
.
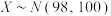 .已知参加本次考试的学生约有9450人,如果某学生在这次考试中数学成绩为108分,那么他的数学成绩大约排在该区的名次是
.已知参加本次考试的学生约有9450人,如果某学生在这次考试中数学成绩为108分,那么他的数学成绩大约排在该区的名次是 ,则
,则 ,
,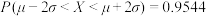 .
.
您最近一年使用:0次
2023-01-03更新
|
2080次组卷
|
8卷引用:云南省昆明市官渡区艺卓中学2023届高三下学期第二次月考数学试题
云南省昆明市官渡区艺卓中学2023届高三下学期第二次月考数学试题沪教版(2020) 选修第二册 堂堂清 第7章 7.3(3)常用分布(正态分布)(已下线)2023年四省联考变试题11-16(已下线)7.5 正态分布(分层作业)(已下线)7.5 正态分布 (精讲)(1)浙江省金华十校2022-2023学年高三下学期4月模拟考试预演数学试题(已下线)上海市静安区2023届高三二模数学试题变式题11-15江苏省南京市人民中学、海安市实验中学、句容市第三中学、镇江心湖高级中学2022-2023学年高二下学期5月联考数学试题
2 . 云南省2016年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布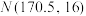 .现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5 cm之间,将测量结果按如下方式分成6组:第一组 [157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],图是按上述分组方法得到的频率分布直方图.
.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5 cm之间,将测量结果按如下方式分成6组:第一组 [157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],图是按上述分组方法得到的频率分布直方图.
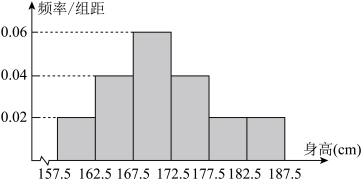
(1)试评估我校高三年级男生在全省高中男生中的平均身高状况;
(2)求这50名男生身高在177.5cm以上(含177.5 cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5 cm)的人中任意抽取2人,求这2人的身高排名(从高到低)均在全省前130名的概率.
参考数据:若 ,则
,则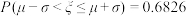 ,
, ,
,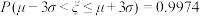 .
.
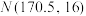 .现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5 cm之间,将测量结果按如下方式分成6组:第一组 [157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],图是按上述分组方法得到的频率分布直方图.
.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5 cm之间,将测量结果按如下方式分成6组:第一组 [157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],图是按上述分组方法得到的频率分布直方图.
(1)试评估我校高三年级男生在全省高中男生中的平均身高状况;
(2)求这50名男生身高在177.5cm以上(含177.5 cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5 cm)的人中任意抽取2人,求这2人的身高排名(从高到低)均在全省前130名的概率.
参考数据:若
 ,则
,则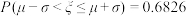 ,
, ,
,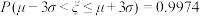 .
.
您最近一年使用:0次
2022-12-26更新
|
554次组卷
|
2卷引用:云南省昆明市第三中学2022届高三上学期第四次综合测试数学(文)试题
名校
3 . 为普及传染病防治知识,增强市民的疾病防范意识,提高自身保护能力,某市举办传染病防治知识有奖竞赛.现从该市所有参赛者中随机抽取了100名参赛者的竞赛成绩,并以此为样本绘制了如表所示的频率分布表.
(1)求这100名参赛者的竞赛成绩的样本均值 和样本方差
和样本方差 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若该市所有参赛者的成绩X近似地服从正态分布 ,用样本估计总体,
,用样本估计总体, 近似为样本均值,
近似为样本均值, 近似为样本方差,利用所得正态分布模型解决以下问题:(参考数据:
近似为样本方差,利用所得正态分布模型解决以下问题:(参考数据: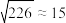 )
)
①如果按照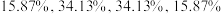 的比例将参赛者的竞赛成绩划分为参与奖、二等奖、一等奖、特等奖四个等级,试确定各等级的分数线(精确到整数);
的比例将参赛者的竞赛成绩划分为参与奖、二等奖、一等奖、特等奖四个等级,试确定各等级的分数线(精确到整数);
②若该市共有10000名市民参加了竞赛,试估计参赛者中获得特等奖的人数(结果四舍五入到整数).
附:若随机变量X服从正态分布 ,则
,则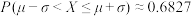 ,
,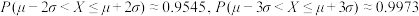 .
.
| 竞赛成绩 | 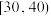 | 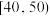 | 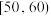 | 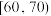 | 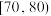 | 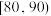 |  |
| 人数 | 6 | 10 | 18 | 33 | 16 | 11 | 6 |
 和样本方差
和样本方差 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(2)若该市所有参赛者的成绩X近似地服从正态分布
 ,用样本估计总体,
,用样本估计总体, 近似为样本均值,
近似为样本均值, 近似为样本方差,利用所得正态分布模型解决以下问题:(参考数据:
近似为样本方差,利用所得正态分布模型解决以下问题:(参考数据: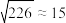 )
)①如果按照
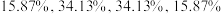 的比例将参赛者的竞赛成绩划分为参与奖、二等奖、一等奖、特等奖四个等级,试确定各等级的分数线(精确到整数);
的比例将参赛者的竞赛成绩划分为参与奖、二等奖、一等奖、特等奖四个等级,试确定各等级的分数线(精确到整数);②若该市共有10000名市民参加了竞赛,试估计参赛者中获得特等奖的人数(结果四舍五入到整数).
附:若随机变量X服从正态分布
 ,则
,则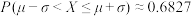 ,
,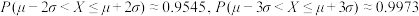 .
.
您最近一年使用:0次
2022-05-02更新
|
737次组卷
|
4卷引用:云南师范大学附属中学2021-2022学年高二下学期期中数学试题
云南师范大学附属中学2021-2022学年高二下学期期中数学试题云南省保山市普通高(完)中2023届高三上学期期末质量监测数学试题(已下线)7.5 正态分布 (精讲)(2)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
4 . 某物流公司专营从甲地到乙地的货运业务(货物全部用统一规格的包装箱包装),现统计了最近100天内每天可配送的货物量,按照可配送的货物量 (单位:箱)分成了以下几组:
(单位:箱)分成了以下几组: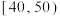 ,
, ,
, ,
, ,
, ,
, ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).

(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析每日的可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自 这一组的概率.
这一组的概率.
(2)由频率分布直方图可以认为,该物流公司每日的可配送货物量 (单位:箱)近似服从正态分布
(单位:箱)近似服从正态分布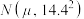 ,其中
,其中 近似为样本平均数.
近似为样本平均数.
(i)试利用该正态分布,估计该物流公司2000天内日货物配送量在区间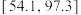 内的天数(结果保留整数).
内的天数(结果保留整数).
附:若 ,则
,则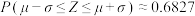 ,
,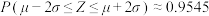 .
.
(ii)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为三级,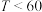 时,奖励50元;
时,奖励50元;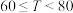 时,奖励80元;
时,奖励80元; 时,奖励120元.
时,奖励120元.
方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于 时只有一次抽奖机会,每次抽奖的奖金及对应的概率为
时只有一次抽奖机会,每次抽奖的奖金及对应的概率为
小张为该公司装卸货物的一名员工,试从数学期望的角度分析,小张选择哪种奖励方案对他更有利?
 (单位:箱)分成了以下几组:
(单位:箱)分成了以下几组: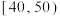 ,
, ,
, ,
, ,
, ,
, ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析每日的可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自
 这一组的概率.
这一组的概率.(2)由频率分布直方图可以认为,该物流公司每日的可配送货物量
 (单位:箱)近似服从正态分布
(单位:箱)近似服从正态分布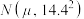 ,其中
,其中 近似为样本平均数.
近似为样本平均数.(i)试利用该正态分布,估计该物流公司2000天内日货物配送量在区间
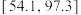 内的天数(结果保留整数).
内的天数(结果保留整数).附:若
 ,则
,则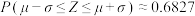 ,
,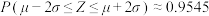 .
.(ii)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为三级,
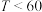 时,奖励50元;
时,奖励50元;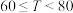 时,奖励80元;
时,奖励80元; 时,奖励120元.
时,奖励120元.方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于
 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于 时只有一次抽奖机会,每次抽奖的奖金及对应的概率为
时只有一次抽奖机会,每次抽奖的奖金及对应的概率为奖金 | 50 | 100 |
概率 |
|
|
您最近一年使用:0次
2021-09-23更新
|
599次组卷
|
9卷引用:云南民族大学附属中学2022届高三高考押题卷二数学(理)试题
云南民族大学附属中学2022届高三高考押题卷二数学(理)试题2019届安徽师范大学附属中学高三下学期高考前适应性检测数学(理)试题湖北省黄石市第二中学2019-2020学年高二下学期5月月考数学(理)试题(已下线)专题34 正态分布-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练人教A版(2019) 选修第三册 突围者 第七章 专项 均值与方差在决策问题中的应用黑龙江省哈尔滨市第六中学2021届高三第四次模拟数学(理)试题山东省2021-2022学年高三10月“山东学情”联考数学试题C广西师范大学附属外国语学校2022届高三5月适应性模拟测试数学试题(已下线)第05讲 离散型随机变量及其分布列(核心考点讲与练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)
5 . 为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布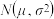 .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在 之外的零件数,求
之外的零件数,求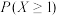 及X的数学期望;
及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
经计算得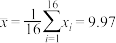 ,
,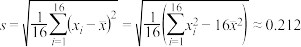 ,其中xi为抽取的第i个零件的尺寸,
,其中xi为抽取的第i个零件的尺寸,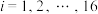 .
.
用样本平均数 作为μ的估计值
作为μ的估计值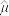 ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布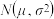 ,则
,则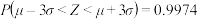 ,
,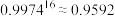 ,
,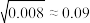 .
.
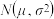 .
.(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在
 之外的零件数,求
之外的零件数,求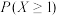 及X的数学期望;
及X的数学期望;(2)一天内抽检零件中,如果出现了尺寸在
 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
| 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
| 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
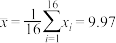 ,
,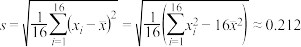 ,其中xi为抽取的第i个零件的尺寸,
,其中xi为抽取的第i个零件的尺寸,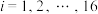 .
.用样本平均数
 作为μ的估计值
作为μ的估计值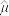 ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).附:若随机变量Z服从正态分布
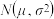 ,则
,则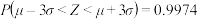 ,
,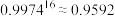 ,
,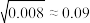 .
.
您最近一年使用:0次
2020-07-11更新
|
20605次组卷
|
64卷引用:云南省红河州泸西一中2017─2018学年高二上学期期末考试理科数学试题
云南省红河州泸西一中2017─2018学年高二上学期期末考试理科数学试题甘肃省兰州市第一中学2016-2017学年高二下学期期末考试数学(理)试题2017年全国普通高等学校招生统一考试理科数学(新课标1卷精编版)甘肃省兰州市第十中学2016-2017学年第二学期期末考试高二数学(理)试题2018年高考数学(理科,通用版)练酷专题二轮复习课时跟踪检测:(二十) 概率与统计【全国百强校】宁夏银川一中2017-2018学年高二下学期期中数学(理)试卷(已下线)《考前20天终极攻略》5月30日 概率【理科】(已下线)《高频考点解密》—解密25 概率福建省泰宁第一中学2019-2020学年高二下学期第一次阶段考试数学试题(已下线)考点38 正态分布和条件概率(练习)-2021年高考数学复习一轮复习笔记(已下线)突破2.4正态分步-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)突破2.4正态分布突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)综合测试卷(巅峰版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)专题16 概率与统计综合-五年(2016-2020)高考数学(理)真题分项(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(六)(已下线)专题19 概率与统计综合-2020年高考数学(理)母题题源解密(全国Ⅰ专版)(已下线)专题11.7 二项分布、正态分布(精练)-2021年新高考数学一轮复习学与练(已下线)专题11.7 二项分布、正态分布(练)-2021年新高考数学一轮复习讲练测(已下线)专题11.5 离散型随机变量的分布列、均值与方差(精讲)-2021年高考数学(理)一轮复习学与练(已下线)专题4.5 正态分布(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)新疆昌吉第九中学2021届高三上学期期中考试数学试题(已下线)第二章 随机变量及其分布【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)北师大版(2019) 选修第一册 必杀技 第六章 素养检测人教A版(2019) 选修第三册 必杀技 第七章检测(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)考向49 二项分布与正态分布(已下线)专题09 计数原理与概率与统计(理)-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)专题47 概率、随机变量及其分布-备战2022年高考数学一轮复习一网打尽之重点难点突破(已下线)专题46 随机变量及其分布-学会解题之高三数学万能解题模板【2022版】(已下线)第14讲 正态分布-【寒假自学课】2022年高二数学寒假精品课(苏教版2019选择性必修第二册)(已下线)复习题三4(已下线)专题20统计概率(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲(已下线)第七章 随机变量及其分布(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(人教A版2019选择性必修第三册)(已下线)专题20统计概率解答题20题-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)专题52 盘点随机变量分布列及期望的问题——备战2022年高考数学二轮复习常考点专题突破人教A版(2019) 选修第三册 一蹴而就 第七章 单元整合(已下线)专题1 概率、二项分布与正态分布-学会解题之高三数学321训练体系【2022版】人教A版(2019) 选修第三册 过关斩将 第七章 7.4~7.5综合拔高练(已下线)解密16 随机变量及其分布(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)江苏省盐城市滨海中学2019-2020学年高二下学期期末模拟数学试题江苏省徐州市2022届高三下学期打靶试卷数学试题安徽省合肥市第八中学2022届高三下学期最后一卷保温理科数学试题(已下线)专题50:正态分布-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题49:离散随机变量的均值与方差-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题13 概率统计解答题(已下线)考点26 概率、二项分布与正态分布-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)2023版 湘教版(2019) 选修第二册 过关斩将 第3章 综合拔高练(已下线)考向42 四大分布:两点分布、二项分布、超几何分布与正态分布(十大经典题型)-3(已下线)考向43二项分布、正太分布及其应用(重点)-3(已下线)考向42离散型随机变量的期望与方差(重点)-2(已下线)13.4 正态分布(已下线)第72讲 正态分布(已下线)专题11-1 直方图、回归方程(线性与非线性)-2(已下线)专题25 统计类(解答题)+概率(几何概型)-3(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-3(已下线)第四篇 概率与统计 专题7 常见分布 微点1 常见分布(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(练习)单元测试B卷——第七章 随机变量及其分布(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)江苏省海安高级中学2023-2024学年高二下学期期中考试数学试卷(已下线)专题25 概率统计解答题(理科)-2专题32概率统计解答题(第一部分)【巩固卷】第3章 概率高考强化 单元测试B-湘教版(2019)选择性必修第二册(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(练习)-2
名校
6 . 某工厂抽取了一台设备 在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
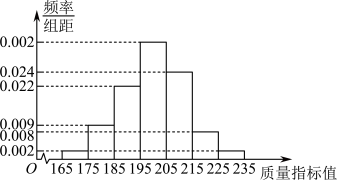
(1)计算该样本的平均值 ,方差
,方差 ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)根据长期生产经验,可以认为这台设备在正常状态下生产的产品的质量指标值服从正态分布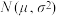 ,其中
,其中 近似为样本平均值,
近似为样本平均值, 近似为样本方差
近似为样本方差 .任取一个产品,记其质量指标值为
.任取一个产品,记其质量指标值为 .若
.若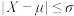 ,则认为该产品为一等品;
,则认为该产品为一等品;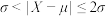 ,则认为该产品为二等品;若
,则认为该产品为二等品;若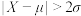 ,则认为该产品为不合格品.已知设备
,则认为该产品为不合格品.已知设备 正常状态下每天生产这种产品1000个.
正常状态下每天生产这种产品1000个.
(i)用样本估计总体,问该工厂一天生产的产品中不合格品是否超过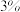 ?
?
(ii)某公司向该工厂推出以旧换新活动,补足50万元即可用设备 换得生产相同产品的改进设备
换得生产相同产品的改进设备 .经测试,设备
.经测试,设备 正常状态下每天生产产品1200个,生产的产品为一等品的概率是
正常状态下每天生产产品1200个,生产的产品为一等品的概率是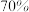 ,二等品的概率是
,二等品的概率是 ,不合格品的概率是
,不合格品的概率是 .若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备
.若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备 ?
?
参考数据:① ;②
;②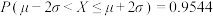 ;③
;③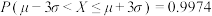 ,
,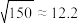 .
.
 在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
(1)计算该样本的平均值
 ,方差
,方差 ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)(2)根据长期生产经验,可以认为这台设备在正常状态下生产的产品的质量指标值服从正态分布
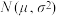 ,其中
,其中 近似为样本平均值,
近似为样本平均值, 近似为样本方差
近似为样本方差 .任取一个产品,记其质量指标值为
.任取一个产品,记其质量指标值为 .若
.若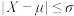 ,则认为该产品为一等品;
,则认为该产品为一等品;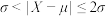 ,则认为该产品为二等品;若
,则认为该产品为二等品;若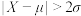 ,则认为该产品为不合格品.已知设备
,则认为该产品为不合格品.已知设备 正常状态下每天生产这种产品1000个.
正常状态下每天生产这种产品1000个.(i)用样本估计总体,问该工厂一天生产的产品中不合格品是否超过
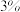 ?
?(ii)某公司向该工厂推出以旧换新活动,补足50万元即可用设备
 换得生产相同产品的改进设备
换得生产相同产品的改进设备 .经测试,设备
.经测试,设备 正常状态下每天生产产品1200个,生产的产品为一等品的概率是
正常状态下每天生产产品1200个,生产的产品为一等品的概率是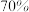 ,二等品的概率是
,二等品的概率是 ,不合格品的概率是
,不合格品的概率是 .若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备
.若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备 ?
?参考数据:①
 ;②
;②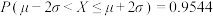 ;③
;③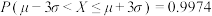 ,
,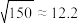 .
.
您最近一年使用:0次
2019-05-19更新
|
787次组卷
|
4卷引用:【全国百强校】云南省师范大学附属中学2019届高三第八次月考数学(理)试题
【全国百强校】云南省师范大学附属中学2019届高三第八次月考数学(理)试题北师大版(2019) 选修第一册 必杀技 第六章 素养检测人教A版(2019) 选修第三册 必杀技 第七章检测(已下线)考点18 决策的选择问题 2024届高考数学考点总动员【练】





