名校
1 . 某企业使用新技术对某款芯片制造工艺进行改进.部分芯片由智能检测系统进行筛选,其中部分次品芯片会被淘汰,筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记 表示事件“某芯片通过智能检测系统筛选”,
表示事件“某芯片通过智能检测系统筛选”, 表示事件“某芯片经人工抽检后合格”.改进生产工艺后,该款芯片的某项质量指标
表示事件“某芯片经人工抽检后合格”.改进生产工艺后,该款芯片的某项质量指标 服从正态分布
服从正态分布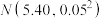 ,现从中随机抽取
,现从中随机抽取 个,这
个,这 个芯片中恰有
个芯片中恰有 个的质量指标
个的质量指标 位于区间
位于区间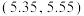 ,则下列说法正确的是( )(若
,则下列说法正确的是( )(若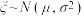 ,
, )
)
 表示事件“某芯片通过智能检测系统筛选”,
表示事件“某芯片通过智能检测系统筛选”, 表示事件“某芯片经人工抽检后合格”.改进生产工艺后,该款芯片的某项质量指标
表示事件“某芯片经人工抽检后合格”.改进生产工艺后,该款芯片的某项质量指标 服从正态分布
服从正态分布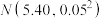 ,现从中随机抽取
,现从中随机抽取 个,这
个,这 个芯片中恰有
个芯片中恰有 个的质量指标
个的质量指标 位于区间
位于区间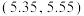 ,则下列说法正确的是( )(若
,则下列说法正确的是( )(若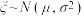 ,
, )
)A. |
B. |
C.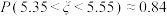 |
D. 取得最大值时, 取得最大值时, 的估计值为53 的估计值为53 |
您最近一年使用:0次
2024-05-17更新
|
1576次组卷
|
12卷引用:第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)江苏省决胜新高考2024届高三下学期4月大联考数学试题江苏省常州市金坛第四中学2024届高三考前适应性考试(三模)数学试题江苏省如东县、宿迁一中、沭阳如东中学2023-2024学年高三下学期期中学情检测数学试题湖南省长沙市第一中学2023-2024学年高三下学期2月开学考试数学试卷(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题09 计数原理与随机变量及分布列(讲义)重庆市乌江新高考协作体2023-2024学年高二下学期第一阶段学业质量联合调研抽测(4月)数学试题单元测试B卷——第七章 随机变量及其分布重庆市涪陵第五中学校2024届高三下学期第二次适应性考试数学试题(已下线)暑假作业08 二项分布、超几何分布及正态分布-【暑假分层作业】(人教A版2019)安徽省合肥市第一中学瑶海校区2023-2024学年高二下学期数学素质拓展训练(五)
名校
解题方法
2 . 已知某种机器的电源电压U(单位:V)服从正态分布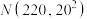 .其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
.其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
(1)求该机器生产的零件为不合格品的概率;
(2)从该机器生产的零件中随机抽取n( )件,记其中恰有2件不合格品的概率为
)件,记其中恰有2件不合格品的概率为 ,求
,求 取得最大值时n的值.
取得最大值时n的值.
附:若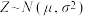 ,取
,取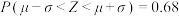 ,
,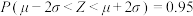 .
.
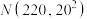 .其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
.其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.(1)求该机器生产的零件为不合格品的概率;
(2)从该机器生产的零件中随机抽取n(
 )件,记其中恰有2件不合格品的概率为
)件,记其中恰有2件不合格品的概率为 ,求
,求 取得最大值时n的值.
取得最大值时n的值.附:若
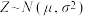 ,取
,取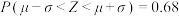 ,
,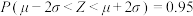 .
.
您最近一年使用:0次
2024-03-22更新
|
3403次组卷
|
6卷引用:江苏省南京市、盐城市2024届高三第一次模拟考试数学试题
江苏省南京市、盐城市2024届高三第一次模拟考试数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)7.5正态分布 第三课 知识扩展延伸(已下线)数学(广东专用01,新题型结构)(已下线)专题3.4正态分布(五个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)陕西省西安市陕西师范大学附属中学2023-2024学年高二下学期期中考试数学试卷
2024高三下·江苏·专题练习
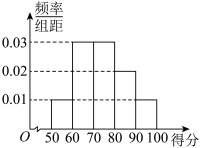
3 . 2023年,全国政协十四届一次会议于3月4日下午3时在人民大会堂开幕,3月11日下午闭幕,会期7天半;十四届全国人大一次会议于3月5日上午开幕,13日上午闭幕,会期8天半.为调查居民对两会相关知识的了解情况,某小区开展了两会知识问答活动,现将该小区参与该活动的240位居民的得分(满分100分)进行了统计,得到如下的频率分布直方图.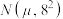 ,其中
,其中 近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求
近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求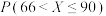 的值;
的值;
(2)中国移动为支持本次活动提供了大力支持,制定了如下奖励方案:参与本次活动得分低于 的居民获得一次抽奖机会,参与本次活动得分不低于
的居民获得一次抽奖机会,参与本次活动得分不低于 的居民获得两次抽奖机会,每位居民每次有
的居民获得两次抽奖机会,每位居民每次有 的机会抽中一张10元的话费充值卡,有
的机会抽中一张10元的话费充值卡,有 的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y(单位:元)的概率分布列,并估计本次活动中国移动需要准备的话费充值卡的总金额(单位:元)
的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y(单位:元)的概率分布列,并估计本次活动中国移动需要准备的话费充值卡的总金额(单位:元)
参考数据: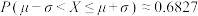 ,
,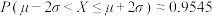 ,
,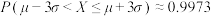 .
.
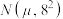 ,其中
,其中 近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求
近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求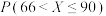 的值;
的值;(2)中国移动为支持本次活动提供了大力支持,制定了如下奖励方案:参与本次活动得分低于
 的居民获得一次抽奖机会,参与本次活动得分不低于
的居民获得一次抽奖机会,参与本次活动得分不低于 的居民获得两次抽奖机会,每位居民每次有
的居民获得两次抽奖机会,每位居民每次有 的机会抽中一张10元的话费充值卡,有
的机会抽中一张10元的话费充值卡,有 的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y(单位:元)的概率分布列,并估计本次活动中国移动需要准备的话费充值卡的总金额(单位:元)
的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y(单位:元)的概率分布列,并估计本次活动中国移动需要准备的话费充值卡的总金额(单位:元)参考数据:
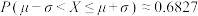 ,
,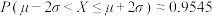 ,
,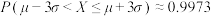 .
.
您最近一年使用:0次
2024-03-17更新
|
853次组卷
|
6卷引用:专题11 统计与概率(分层练)
(已下线)专题11 统计与概率(分层练)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)吉林省长春市绿园区长春市文理高中2023-2024学年高二下学期4月月考数学试题(已下线)专题3.4正态分布(五个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)四川省眉山市仁寿县两校2024届高三下学期第三次模拟理科数学试题(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)
2024·安徽安庆·二模
4 . 树人高中拟组织学生到某航天基地开展天宫模拟飞行器体验活动,该项活动对学生身体体能指标和航天知识素养有明确要求.学校所有3000名学生参加了遴选活动,遴选活动分以下两个环节,当两个环节均测试合格可以参加体验活动.
第一环节:对学生身体体能指标进行测试,当测试值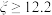 时体能指标合格;
时体能指标合格;
第二环节:对身体体能指标符合要求的学生进行航天知识素养测试,测试方案为对A,B两类试题依次作答,均测试合格才能符合遴选要求.每类试题均在题库中随机产生,有两次测试机会,在任一类试题测试中,若第一次测试合格,不再进行第二次测试.若第一次测试不合格,则进行第二次测试,若第二次测试合格,则该类试题测试合格,若第二次测试不合格,则该类试题测试不合格,测试结束.
经过统计,该校学生身体体能指标 服从正态分布
服从正态分布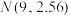 .
.
参考数值: ,
,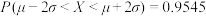 ,
, .
.
(1)请估计树人高中遴选学生符合身体体能指标的人数(结果取整数);
(2)学生小华通过身体体能指标遴选,进入航天知识素养测试,作答A类试题,每次测试合格的概率为 ,作答B类试题,每次测试合格的概率为
,作答B类试题,每次测试合格的概率为 ,且每次测试相互独立.
,且每次测试相互独立.
①在解答A类试题第一次测试合格的条件下,求测试共进行3次的概率.
②若解答A、B两类试题测试合格的类数为X,求X的分布列和数学期望.
第一环节:对学生身体体能指标进行测试,当测试值
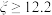 时体能指标合格;
时体能指标合格;第二环节:对身体体能指标符合要求的学生进行航天知识素养测试,测试方案为对A,B两类试题依次作答,均测试合格才能符合遴选要求.每类试题均在题库中随机产生,有两次测试机会,在任一类试题测试中,若第一次测试合格,不再进行第二次测试.若第一次测试不合格,则进行第二次测试,若第二次测试合格,则该类试题测试合格,若第二次测试不合格,则该类试题测试不合格,测试结束.
经过统计,该校学生身体体能指标
 服从正态分布
服从正态分布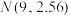 .
.参考数值:
 ,
,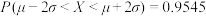 ,
, .
.(1)请估计树人高中遴选学生符合身体体能指标的人数(结果取整数);
(2)学生小华通过身体体能指标遴选,进入航天知识素养测试,作答A类试题,每次测试合格的概率为
 ,作答B类试题,每次测试合格的概率为
,作答B类试题,每次测试合格的概率为 ,且每次测试相互独立.
,且每次测试相互独立.①在解答A类试题第一次测试合格的条件下,求测试共进行3次的概率.
②若解答A、B两类试题测试合格的类数为X,求X的分布列和数学期望.
您最近一年使用:0次
名校
解题方法
5 . 某商场将在“周年庆”期间举行“购物刮刮乐,龙腾旺旺来”活动,活动规则:顾客投掷3枚质地均匀的股子.若3枚骰子的点数都是奇数,则中“龙腾奖”,获得两张“刮刮乐”;若3枚骰子的点数之和为6的倍数,则中“旺旺奖”,获得一张“刮刮乐”;其他情况不获得“刮刮乐”.
(1)据往年统计,顾客消费额 (单位:元)服从正态分布
(单位:元)服从正态分布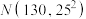 .若某天该商场有20000位顾客,请估计该天消费额
.若某天该商场有20000位顾客,请估计该天消费额 在
在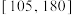 内的人数;
内的人数;
附:若 ,则
,则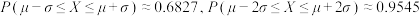 .
.
(2)已知每张“刮刮乐”刮出甲奖品的概率为 ,刮出乙奖品的概率为
,刮出乙奖品的概率为 .
.
①求顾客获得乙奖品的概率;
②若顾客已获得乙奖品,求其是中“龙腾奖”而获得的概率.
(1)据往年统计,顾客消费额
 (单位:元)服从正态分布
(单位:元)服从正态分布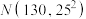 .若某天该商场有20000位顾客,请估计该天消费额
.若某天该商场有20000位顾客,请估计该天消费额 在
在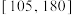 内的人数;
内的人数;附:若
 ,则
,则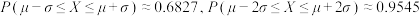 .
.(2)已知每张“刮刮乐”刮出甲奖品的概率为
 ,刮出乙奖品的概率为
,刮出乙奖品的概率为 .
.①求顾客获得乙奖品的概率;
②若顾客已获得乙奖品,求其是中“龙腾奖”而获得的概率.
您最近一年使用:0次
2024-03-12更新
|
1893次组卷
|
5卷引用:8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)福建省莆田市2024届高三毕业班第二次教学质量检测数学试卷(已下线)7.5正态分布 第三练 能力提升拔高福建省福州市八县(市、区)协作校2023-2024学年高二下学期期中联考数学试题(已下线)高二下学期第三次月考(范围:选择性必修二、三)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
6 . 某制造商生产的5000根金属棒的长度近似服从正态分布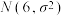 ,其中恰有114根金属棒长度不小于6.04.
,其中恰有114根金属棒长度不小于6.04.
(1)求 ;
;
(2)如果允许制造商生产这种金属棒的长度范围是(5.95,6.05),那么这批金属棒中不合格的金属棒约有多少根?
说明:对任何一个正态分布 来说,通过
来说,通过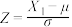 转化为标准正态分布
转化为标准正态分布 ,从而查标准正态分布表得到
,从而查标准正态分布表得到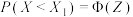 .
.
可供查阅的(部分)标准正态分布表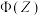
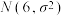 ,其中恰有114根金属棒长度不小于6.04.
,其中恰有114根金属棒长度不小于6.04.(1)求
 ;
;(2)如果允许制造商生产这种金属棒的长度范围是(5.95,6.05),那么这批金属棒中不合格的金属棒约有多少根?
说明:对任何一个正态分布
 来说,通过
来说,通过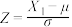 转化为标准正态分布
转化为标准正态分布 ,从而查标准正态分布表得到
,从而查标准正态分布表得到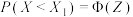 .
.可供查阅的(部分)标准正态分布表
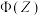
| 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 |
| 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 | 0.9713 |
| 2.0 | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 |
| 0.9772 | 0.9821 | 0.9861 | 0.9893 | 0.9918 | 0.9938 | 0.9953 | 0.9965 | 0.9974 |
您最近一年使用:0次
名校
解题方法
7 . 在工业生产中轴承的直径服从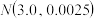 ,购买者要求直径为
,购买者要求直径为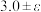 ,不在这个范围的将被拒绝,要使拒绝的概率控制在
,不在这个范围的将被拒绝,要使拒绝的概率控制在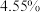 之内,则
之内,则 至少为
至少为_________ ;(若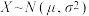 ,则
,则 )
)
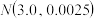 ,购买者要求直径为
,购买者要求直径为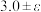 ,不在这个范围的将被拒绝,要使拒绝的概率控制在
,不在这个范围的将被拒绝,要使拒绝的概率控制在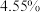 之内,则
之内,则 至少为
至少为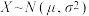 ,则
,则 )
)
您最近一年使用:0次
2024-02-04更新
|
2118次组卷
|
9卷引用:8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)信息必刷卷02(江苏专用,2024新题型)新疆维吾尔自治区乌鲁木齐市2024届高三第一次质量监测数学试题湖北省十堰市郧阳中学2024届高三上学期期末数学试题(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)黑龙江省大庆市大庆中学2024届高三下学期开学考试数学试题(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题08 平面向量、概率、统计、计数原理河南省开封市五县六校2023-2024学年高二下学期6月联考数学试题
8 . 某保险公司有一款保险产品,该产品今年保费为200元/人,赔付金额为5万元/人.假设该保险产品的客户为10000名,每人被赔付的概率均为 ,记10000名客户中获得赔偿的人数为
,记10000名客户中获得赔偿的人数为 .
.
(1)求 ,并计算该公司今年这一款保险产品利润的期望;
,并计算该公司今年这一款保险产品利润的期望;
(2)二项分布是离散型的,而正态分布是连续型的,它们是不同的概率分布,但是,随着二项分布的试验次数的增加,二项分布折线图与正态分布曲线几乎一致,所以当试验次数较大时,可以利用正态分布处理二项分布的相关概率计算问题,我们知道若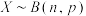 ,则
,则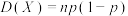 ,当
,当 较大且
较大且 较小时,我们为了简化计算,常用
较小时,我们为了简化计算,常用 的值估算
的值估算 的值.
的值.
请根据上述信息,求:
①该公司今年这一款保险产品利润为50~100万元的概率;
②该公司今年这一款保险产品亏损的概率.
参考数据:若 ,则
,则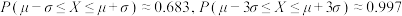 .
.
 ,记10000名客户中获得赔偿的人数为
,记10000名客户中获得赔偿的人数为 .
.(1)求
 ,并计算该公司今年这一款保险产品利润的期望;
,并计算该公司今年这一款保险产品利润的期望;(2)二项分布是离散型的,而正态分布是连续型的,它们是不同的概率分布,但是,随着二项分布的试验次数的增加,二项分布折线图与正态分布曲线几乎一致,所以当试验次数较大时,可以利用正态分布处理二项分布的相关概率计算问题,我们知道若
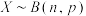 ,则
,则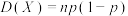 ,当
,当 较大且
较大且 较小时,我们为了简化计算,常用
较小时,我们为了简化计算,常用 的值估算
的值估算 的值.
的值.请根据上述信息,求:
①该公司今年这一款保险产品利润为50~100万元的概率;
②该公司今年这一款保险产品亏损的概率.
参考数据:若
 ,则
,则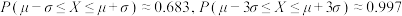 .
.
您最近一年使用:0次
2024-01-29更新
|
679次组卷
|
6卷引用:江苏省扬州市2024届高三上学期期末检测数学试题
江苏省扬州市2024届高三上学期期末检测数学试题(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)第08讲 7.5 正态分布(3)(已下线)第08讲 7.5 正态分布(2)(已下线)7.5 正态分布——课后作业(提升版)
9 . 为了检测自动包装线生产的罐装咖啡,检验员每天从生产线上随机抽取 罐咖啡,并测量其质量(单位:
罐咖啡,并测量其质量(单位: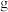 ).由于存在各种不可控制的因素,任意抽取的1罐咖啡的质量与标准质量之间存在一定的误差,已知这条包装线在正常状态下,每罐咖啡的质量服从正态分布
).由于存在各种不可控制的因素,任意抽取的1罐咖啡的质量与标准质量之间存在一定的误差,已知这条包装线在正常状态下,每罐咖啡的质量服从正态分布 .假设生产状态正常,记
.假设生产状态正常,记 表示每天抽取的
表示每天抽取的 罐咖啡中质量在
罐咖啡中质量在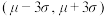 之外的罐数,若
之外的罐数,若 的数学期望
的数学期望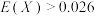 ,则
,则 的最小值为( )
的最小值为( )
附:若随机变量 服从正态分布
服从正态分布 ,则
,则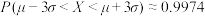 .
.
 罐咖啡,并测量其质量(单位:
罐咖啡,并测量其质量(单位: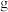 ).由于存在各种不可控制的因素,任意抽取的1罐咖啡的质量与标准质量之间存在一定的误差,已知这条包装线在正常状态下,每罐咖啡的质量服从正态分布
).由于存在各种不可控制的因素,任意抽取的1罐咖啡的质量与标准质量之间存在一定的误差,已知这条包装线在正常状态下,每罐咖啡的质量服从正态分布 .假设生产状态正常,记
.假设生产状态正常,记 表示每天抽取的
表示每天抽取的 罐咖啡中质量在
罐咖啡中质量在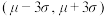 之外的罐数,若
之外的罐数,若 的数学期望
的数学期望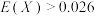 ,则
,则 的最小值为( )
的最小值为( )附:若随机变量
 服从正态分布
服从正态分布 ,则
,则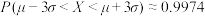 .
.| A.10 | B.11 | C.12 | D.13 |
您最近一年使用:0次
2024-01-25更新
|
480次组卷
|
5卷引用:8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)河南省南阳地区2023-2024学年高二上学期期末热身摸底联考数学试题(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)高二下学期期中复习选择题压轴题十五大题型专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题03 随机变量及其分布列-2
2023·全国·模拟预测
名校
解题方法
10 . 某公司为了解市场对其开发的新产品的需求情况,共调查了250名顾客,采取100分制对产品功能满意程度、产品外观满意程度分别进行评分,其中对产品功能满意程度的评分服从正态分布 ,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.
,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.
(2)若这250人中对两项都非常满意的有2人,现从对产品功能非常满意和对产品外观非常满意的人中随机抽取3人,设3人中两项都非常满意的有X人,求X的分布列和数学期望. (附:若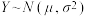 ,则
,则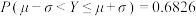 ,
, )
)
 ,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.
,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.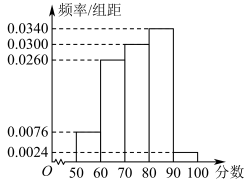
(2)若这250人中对两项都非常满意的有2人,现从对产品功能非常满意和对产品外观非常满意的人中随机抽取3人,设3人中两项都非常满意的有X人,求X的分布列和数学期望. (附:若
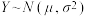 ,则
,则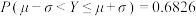 ,
, )
)
您最近一年使用:0次
2024-03-19更新
|
716次组卷
|
7卷引用:8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)2024年全国高考名校名师联席命制型数学信息卷(五)(已下线)2024年全国高考名校名师联席命制数学(理)信息卷(六)江西省上饶市玉山县第二中学2023-2024学年高二上学期12月月考数学试题江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(三)(已下线)专题8-2分布列综合归类-2(已下线)第七章 随机变量及其分布总结 第一练 考点强化训练




