名校
解题方法
1 . (1)证明:函数 为奇函数的充要条件是
为奇函数的充要条件是 .
.
(2)我们知道,函数 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图象关于点
的图象关于点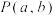 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数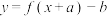 为奇函数.
为奇函数.
①求函数 的图象的对称中心.
的图象的对称中心.
②类比上述推论,写出“函数 的图象关于y轴成轴对称图形的充要条件是函数
的图象关于y轴成轴对称图形的充要条件是函数 为偶函数”的一个推广的结论.
为偶函数”的一个推广的结论.
 为奇函数的充要条件是
为奇函数的充要条件是 .
.(2)我们知道,函数
 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图象关于点
的图象关于点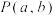 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数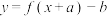 为奇函数.
为奇函数.①求函数
 的图象的对称中心.
的图象的对称中心.②类比上述推论,写出“函数
 的图象关于y轴成轴对称图形的充要条件是函数
的图象关于y轴成轴对称图形的充要条件是函数 为偶函数”的一个推广的结论.
为偶函数”的一个推广的结论.
您最近一年使用:0次
2023-11-05更新
|
146次组卷
|
3卷引用:四川省雅安市天立学校腾飞高中2023-2024学年高一上学期11月月考数学试题
四川省雅安市天立学校腾飞高中2023-2024学年高一上学期11月月考数学试题(已下线)第三章 函数的概念与性质【单元基础卷】-【满分全攻略】(人教A版2019必修第一册)广东省佛山市南海区第一中学2023-2024学年高一上学期第一次阶段考数学试题
解题方法
2 . 椭圆 :
: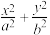 =1(
=1( )的中心在坐标原点,
)的中心在坐标原点, 为左焦点,
为左焦点, 为右顶点,
为右顶点, 为短轴的端点,当
为短轴的端点,当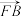 丄
丄 时,椭圆的离心率为
时,椭圆的离心率为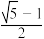 ,我们称此类椭圆为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )
,我们称此类椭圆为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )
 :
: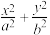 =1(
=1( )的中心在坐标原点,
)的中心在坐标原点, 为左焦点,
为左焦点, 为右顶点,
为右顶点, 为短轴的端点,当
为短轴的端点,当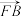 丄
丄 时,椭圆的离心率为
时,椭圆的离心率为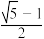 ,我们称此类椭圆为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )
,我们称此类椭圆为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )A.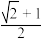 | B.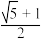 |
C.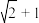 | D.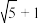 |
您最近一年使用:0次
解题方法
3 . 观察下面的解答过程:已知正实数a,b满足 ,求
,求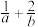 的最小值.
的最小值.
解:∵ ,
,
∴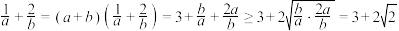 ,
,
当且仅当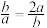 ,结合
,结合 得
得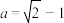 ,
,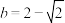 时等号成立,
时等号成立,
∴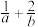 的最小值为
的最小值为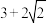 .
.
请类比以上方法,解决下面问题:
(1)已知正实数x,y满足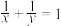 ,求
,求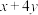 的最小值;
的最小值;
(2)已知正实数x,y满足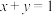 ,求
,求 的最小值.
的最小值.
 ,求
,求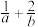 的最小值.
的最小值.解:∵
 ,
, ∴
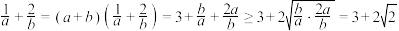 ,
,当且仅当
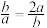 ,结合
,结合 得
得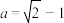 ,
,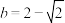 时等号成立,
时等号成立,∴
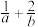 的最小值为
的最小值为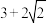 .
.请类比以上方法,解决下面问题:
(1)已知正实数x,y满足
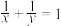 ,求
,求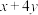 的最小值;
的最小值;(2)已知正实数x,y满足
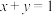 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
4 . 赵爽弦图(如图1)中的大正方形是由4个全等的直角三角形和中间的小正方形拼接而成的,若直角三角形的两条直角边长为a,b,斜边长为c,由大正方形面积等于4个直角三角形的面积与中间小正方形的面积之和可得勾股定理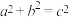 .仿照赵爽弦图构造如图2所示的菱形,它是由两对全等的直角三角形和中间的矩形拼接而成的,设直角三角形的斜边都为1,其中一对直角三角形含有锐角
.仿照赵爽弦图构造如图2所示的菱形,它是由两对全等的直角三角形和中间的矩形拼接而成的,设直角三角形的斜边都为1,其中一对直角三角形含有锐角 ,另一对直角三角形含有锐角
,另一对直角三角形含有锐角 (位置如图2所示).借鉴勾股定理的推导思路可以得到结论( )
(位置如图2所示).借鉴勾股定理的推导思路可以得到结论( )

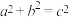 .仿照赵爽弦图构造如图2所示的菱形,它是由两对全等的直角三角形和中间的矩形拼接而成的,设直角三角形的斜边都为1,其中一对直角三角形含有锐角
.仿照赵爽弦图构造如图2所示的菱形,它是由两对全等的直角三角形和中间的矩形拼接而成的,设直角三角形的斜边都为1,其中一对直角三角形含有锐角 ,另一对直角三角形含有锐角
,另一对直角三角形含有锐角 (位置如图2所示).借鉴勾股定理的推导思路可以得到结论( )
(位置如图2所示).借鉴勾股定理的推导思路可以得到结论( )
A.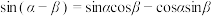 | B.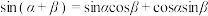 |
C. | D.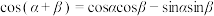 |
您最近一年使用:0次
2022-05-01更新
|
1910次组卷
|
6卷引用:5.5三角恒等变换
5.5三角恒等变换(已下线)【第二练】5.5.1课时1 两角和与差的正弦、余弦公式(已下线)专题2 赵爽弦图(已下线)模块二情境7 发现数学之美广东省2022届高三二模数学试题广东省佛山市南海区桂华中学2022届高三下学期第三次大测数学试题
名校
5 . 我们知道,函数 的图像关于坐标原点成中心对称的充要条件是函数
的图像关于坐标原点成中心对称的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图像关于点
的图像关于点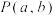 成中心对称的充要条件是函数
成中心对称的充要条件是函数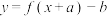 为奇函数.
为奇函数.
(1)求函数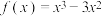 图像的对称中心;
图像的对称中心;
(2)请利用函数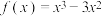 的对称性求
的对称性求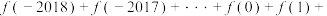
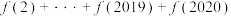 的值.
的值.
(3)类比上述推广结论,写出“函数 的图像关于
的图像关于 轴成轴对称的充要条件是函数
轴成轴对称的充要条件是函数 为偶函数”的一个推广结论.
为偶函数”的一个推广结论.
 的图像关于坐标原点成中心对称的充要条件是函数
的图像关于坐标原点成中心对称的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图像关于点
的图像关于点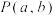 成中心对称的充要条件是函数
成中心对称的充要条件是函数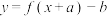 为奇函数.
为奇函数.(1)求函数
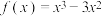 图像的对称中心;
图像的对称中心;(2)请利用函数
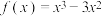 的对称性求
的对称性求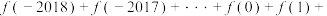
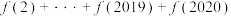 的值.
的值.(3)类比上述推广结论,写出“函数
 的图像关于
的图像关于 轴成轴对称的充要条件是函数
轴成轴对称的充要条件是函数 为偶函数”的一个推广结论.
为偶函数”的一个推广结论.
您最近一年使用:0次
6 . 在《九章算术》方田章圆田术(刘徽注)中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”注述中所用的割圆术是一种无限与有限的转化过程,比如在 中“…”即代表无限次重复,但原式却是个定值
中“…”即代表无限次重复,但原式却是个定值 ,这可以通过方程
,这可以通过方程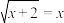 确定出来
确定出来 ,类比上述结论可得
,类比上述结论可得 的正值为( )
的正值为( )
 中“…”即代表无限次重复,但原式却是个定值
中“…”即代表无限次重复,但原式却是个定值 ,这可以通过方程
,这可以通过方程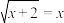 确定出来
确定出来 ,类比上述结论可得
,类比上述结论可得 的正值为( )
的正值为( )| A.1 | B. | C.2 | D.4 |
您最近一年使用:0次
2020-10-23更新
|
509次组卷
|
7卷引用:2023版 北师大版(2019) 必修第一册 突围者 第四章 第一节 对数的概念
2023版 北师大版(2019) 必修第一册 突围者 第四章 第一节 对数的概念安徽省宿州市砀山县第二中学2020-2021学年高三上学期10月月考数学(文)试题安徽省宿州市砀山县第二中学2020-2021学年高三上学期10月月考数学(理)试题(已下线)第十二单元 算法初步与推理证明 (A卷 基础过关检测)-2021年高考数学(文)一轮复习单元滚动双测卷(已下线)第十三单元 算法初步与推理证明 (A卷 基础过关检测)-2021年高考数学(理)一轮复习单元滚动双测卷(已下线)考点42 合情推理与演绎推理-备战2022年高考数学(理)一轮复习考点微专题江西省吉安县立中学2020-2021学年高二12月月考数学(理A)试题
7 . 现新定义两个复数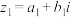 (
( 、
、 )和
)和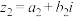 (
( 、
、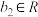 )之间的一个新运算
)之间的一个新运算 ,其运算法则为:
,其运算法则为: .
.
(1)请证明新运算 对于复数的加法满足分配律,即求证:
对于复数的加法满足分配律,即求证: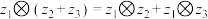 ;
;
(2)设运算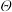 为运算
为运算 的逆运算,请推导运算
的逆运算,请推导运算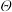 的运算法则.
的运算法则.
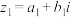 (
( 、
、 )和
)和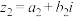 (
( 、
、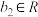 )之间的一个新运算
)之间的一个新运算 ,其运算法则为:
,其运算法则为: .
.(1)请证明新运算
 对于复数的加法满足分配律,即求证:
对于复数的加法满足分配律,即求证: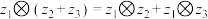 ;
;(2)设运算
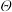 为运算
为运算 的逆运算,请推导运算
的逆运算,请推导运算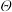 的运算法则.
的运算法则.
您最近一年使用:0次
2020-07-16更新
|
322次组卷
|
6卷引用:沪教版(2020) 必修第二册 同步跟踪练习 第9章 复数 9.1~9.2 阶段综合训练
沪教版(2020) 必修第二册 同步跟踪练习 第9章 复数 9.1~9.2 阶段综合训练苏教版(2019) 必修第二册 必杀技 专练1 新定义、新情境专练沪教版(2020) 必修第二册 同步跟踪练习 第9章 9.1~9.2阶段综合训练(已下线)7.2.2 复数的乘、除运算 (精讲)(2)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)上海市静安区2019-2020学年高二下学期期末数学试题(已下线)第三章 数系的扩充与复数的引入【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-2)
8 . 给出下面类比推理:
①“若 ,则
,则 ”类比推出“若
”类比推出“若 ,则
,则 ”;
”;
②“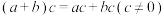 ”类比推出“
”类比推出“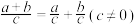 ”;
”;
③“ 、
、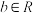 ,若
,若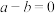 ,则
,则 ”类比推出“
”类比推出“ 、
、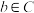 ,若
,若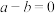 ,则
,则 ”;
”;
④“ 、
、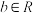 ,若
,若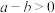 ,则
,则 ”类比推出“
”类比推出“ 、
、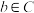 ,若
,若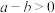 ,则
,则 (
( 为复数集)”.
为复数集)”.
其中结论正确序号的是_______ .
①“若
 ,则
,则 ”类比推出“若
”类比推出“若 ,则
,则 ”;
”;②“
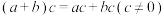 ”类比推出“
”类比推出“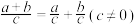 ”;
”;③“
 、
、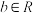 ,若
,若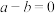 ,则
,则 ”类比推出“
”类比推出“ 、
、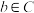 ,若
,若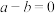 ,则
,则 ”;
”;④“
 、
、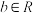 ,若
,若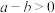 ,则
,则 ”类比推出“
”类比推出“ 、
、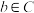 ,若
,若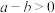 ,则
,则 (
( 为复数集)”.
为复数集)”.其中结论正确序号的是
您最近一年使用:0次
2018高三下·全国·专题练习
名校
9 . 关于圆周率 ,祖冲之的贡献有二:①
,祖冲之的贡献有二:① ;②用
;②用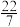 作为约率,
作为约率,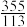 作为密率,其中约率与密率提出了用有理数最佳逼近实数的问题.约率可通过用连分数近似表示的方法得到,如:
作为密率,其中约率与密率提出了用有理数最佳逼近实数的问题.约率可通过用连分数近似表示的方法得到,如: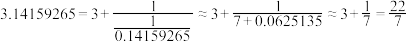 ,舍去0.0625135,得到逼近
,舍去0.0625135,得到逼近 的一个有理数为
的一个有理数为 ,类似地,把
,类似地,把 化为连分数形式:
化为连分数形式: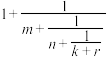 (m,n,k为正整数,r为0到1之间的无理数),舍去r得到逼近
(m,n,k为正整数,r为0到1之间的无理数),舍去r得到逼近 的一个有理数为
的一个有理数为__________ .
 ,祖冲之的贡献有二:①
,祖冲之的贡献有二:① ;②用
;②用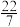 作为约率,
作为约率,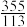 作为密率,其中约率与密率提出了用有理数最佳逼近实数的问题.约率可通过用连分数近似表示的方法得到,如:
作为密率,其中约率与密率提出了用有理数最佳逼近实数的问题.约率可通过用连分数近似表示的方法得到,如: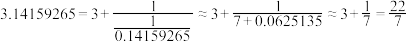 ,舍去0.0625135,得到逼近
,舍去0.0625135,得到逼近 的一个有理数为
的一个有理数为 ,类似地,把
,类似地,把 化为连分数形式:
化为连分数形式: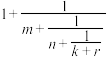 (m,n,k为正整数,r为0到1之间的无理数),舍去r得到逼近
(m,n,k为正整数,r为0到1之间的无理数),舍去r得到逼近 的一个有理数为
的一个有理数为
您最近一年使用:0次
10 . 先阅读下列题目的证法,再解决后面的问题.
已知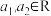 ,且
,且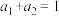 ,求证:
,求证: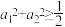 .
.
证明:构造函数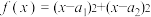 ,
,
则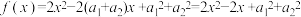 ,
,
因为对一切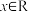 ,恒有
,恒有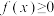 ,
,
所以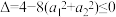 ,
,
从而得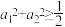 .
.
(1)若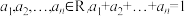 ,请由上述结论写出关于
,请由上述结论写出关于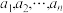 的推广式;
的推广式;
(2)参考上述证法,请对你推广的结论加以证明.
已知
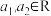 ,且
,且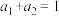 ,求证:
,求证: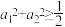 .
.证明:构造函数
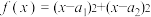 ,
,则
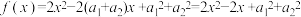 ,
,因为对一切
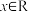 ,恒有
,恒有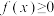 ,
, 所以
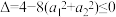 ,
,从而得
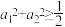 .
.(1)若
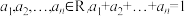 ,请由上述结论写出关于
,请由上述结论写出关于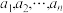 的推广式;
的推广式;(2)参考上述证法,请对你推广的结论加以证明.
您最近一年使用:0次
2018-06-24更新
|
247次组卷
|
13卷引用:上海市浦东新区川沙中学2015-2016学年高一上学期期中数学试题
上海市浦东新区川沙中学2015-2016学年高一上学期期中数学试题沪教版(2020) 必修第一册 达标检测 第二章 章测试(已下线)2013-2014学年湘教版高二数学选修2-2基础达标6.1练习卷2015-2016学年安徽省六安一中高二下第一次段考文数学卷河北省枣强中学2016-2017学年高二下学期期末考试数学(理)试题高中数学人教A版选修2-2 综合复习与测试 (4)陕西省澄城县2017-2018学年高二下学期期中考试数学(理)试题黑龙江省海林市朝鲜族中学人教版高中数学选修1-2同步练习:第二章 推理与证明单元测评河南省南阳市第一中学2021-2022学年高二下学期第二次月考文科数学试题河南省郑州市第十九高级中学2020-2021学年高二下学期3月月考理科数学试题2016-2017学年江西省新余市高二上学期期末考试文数试卷广东省佛山市第三中学2018-2019学年第二学期第一次段考高二理科数学试题安徽省马鞍山二中2018-2019学年高二下学期期中文科数学试题



