名校
1 . 中国古代数学家刘徽在割圆术中提出的“割之弥细所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”,体现了无限与有限之间转化的思想方法,如数式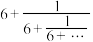 是一个确定值(数式中的省略号表示按此规律无限重复),该数式的值可以用如下方法求得:令原式
是一个确定值(数式中的省略号表示按此规律无限重复),该数式的值可以用如下方法求得:令原式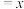 ,则
,则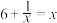 ,即
,即 ,解得
,解得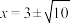 ,取正数得
,取正数得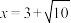 .用类似的方法可得
.用类似的方法可得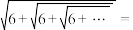
___________ .
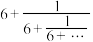 是一个确定值(数式中的省略号表示按此规律无限重复),该数式的值可以用如下方法求得:令原式
是一个确定值(数式中的省略号表示按此规律无限重复),该数式的值可以用如下方法求得:令原式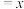 ,则
,则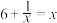 ,即
,即 ,解得
,解得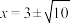 ,取正数得
,取正数得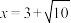 .用类似的方法可得
.用类似的方法可得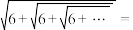
您最近半年使用:0次
2022-06-30更新
|
125次组卷
|
2卷引用:江西省赣州市2021-2022学年高二下学期期末考试数学(文)试题
2 . 已知函数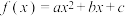 有两个零点
有两个零点 ,则可设
,则可设 ,由
,由 ,所以
,所以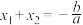 ,
,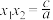 ,这就是一元二次方程根与系数的关系,也称韦达定理,设多项式函数
,这就是一元二次方程根与系数的关系,也称韦达定理,设多项式函数 ,根据代数基本定理可知方程
,根据代数基本定理可知方程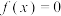 有
有 个根
个根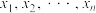 ,则
,则 ( )
( )
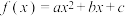 有两个零点
有两个零点 ,则可设
,则可设 ,由
,由 ,所以
,所以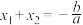 ,
,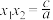 ,这就是一元二次方程根与系数的关系,也称韦达定理,设多项式函数
,这就是一元二次方程根与系数的关系,也称韦达定理,设多项式函数 ,根据代数基本定理可知方程
,根据代数基本定理可知方程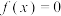 有
有 个根
个根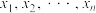 ,则
,则 ( )
( )A.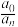 | B. | C.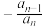 | D.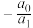 |
您最近半年使用:0次
3 . 下面给出的类比推理中,结论正确的是( )
A.由“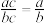 ”类比推出“ ”类比推出“ ” ” |
B.由“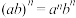 ”类比推出“ ”类比推出“ ” ” |
C.同一平面内,直线 , , , , ,若 ,若 , , ,则 ,则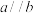 .类比推出:空间中,直线 .类比推出:空间中,直线 , , , , ,若 ,若 , , ,则 ,则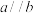 . . |
D.由“若三角形的周长为 ,面积为 ,面积为 ,则其内切圆的半径 ,则其内切圆的半径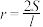 ”类比推出“若三棱锥的表面积为 ”类比推出“若三棱锥的表面积为 ,体积为 ,体积为 ,则内切球的半径 ,则内切球的半径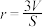 ” ” |
您最近半年使用:0次
2022-06-07更新
|
233次组卷
|
4卷引用:河南省南阳市第一中学2021-2022学年高二下学期第一次月考理科数学试题
4 . 下面给出了关于复数的四种类比推理:
①由多项式的加减法运算,可以类比得到复数的加减法运算;
②由向量 的性质:
的性质: ,可以类比得到复数
,可以类比得到复数 的性质:
的性质: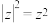 ;
;
③方程 (
( ,且
,且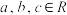 )有两个不等实根的条件是
)有两个不等实根的条件是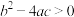 ,类比可得方程
,类比可得方程 (
( ,且
,且 )有两个不等虚根的条件是
)有两个不等虚根的条件是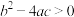 ;
;
④由向量加法的几何意义,可以类比得到复数加法的几何意义.
其中类比得到的结论正确的是( )
①由多项式的加减法运算,可以类比得到复数的加减法运算;
②由向量
 的性质:
的性质: ,可以类比得到复数
,可以类比得到复数 的性质:
的性质: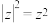 ;
;③方程
 (
( ,且
,且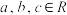 )有两个不等实根的条件是
)有两个不等实根的条件是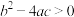 ,类比可得方程
,类比可得方程 (
( ,且
,且 )有两个不等虚根的条件是
)有两个不等虚根的条件是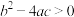 ;
;④由向量加法的几何意义,可以类比得到复数加法的几何意义.
其中类比得到的结论正确的是( )
| A.①③ | B.②④ | C.②③ | D.①④ |
您最近半年使用:0次
名校
5 . 张同学说:因为“ ,则
,则 ”,所以“
”,所以“ ,则
,则 ”.该同学在该推理过程中采用的是
”.该同学在该推理过程中采用的是______ 推理方法.
 ,则
,则 ”,所以“
”,所以“ ,则
,则 ”.该同学在该推理过程中采用的是
”.该同学在该推理过程中采用的是
您最近半年使用:0次
6 . 像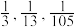 等这样分子为1的分数在算术上称为“单位分数”,数学史上常称为“埃及分数”.1202年意大利数学家斐波那契在他的著作《算盘术》中提到,任何真分数均可表示为有限个埃及分数之和,如
等这样分子为1的分数在算术上称为“单位分数”,数学史上常称为“埃及分数”.1202年意大利数学家斐波那契在他的著作《算盘术》中提到,任何真分数均可表示为有限个埃及分数之和,如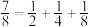 .该结论直到1880年才被英国数学家薛尔维斯特严格证明,实际上,任何真分数分
.该结论直到1880年才被英国数学家薛尔维斯特严格证明,实际上,任何真分数分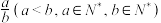 总可表示成
总可表示成 ①,这里
①,这里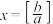 ,即不超过
,即不超过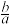 的最大整数,反复利用①式即可将
的最大整数,反复利用①式即可将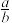 化为若干个“埃及分数”之和.请利用上面的方法将
化为若干个“埃及分数”之和.请利用上面的方法将 表示成3个互不相等的“埃及分数”之和,则
表示成3个互不相等的“埃及分数”之和,则
__________ .
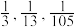 等这样分子为1的分数在算术上称为“单位分数”,数学史上常称为“埃及分数”.1202年意大利数学家斐波那契在他的著作《算盘术》中提到,任何真分数均可表示为有限个埃及分数之和,如
等这样分子为1的分数在算术上称为“单位分数”,数学史上常称为“埃及分数”.1202年意大利数学家斐波那契在他的著作《算盘术》中提到,任何真分数均可表示为有限个埃及分数之和,如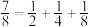 .该结论直到1880年才被英国数学家薛尔维斯特严格证明,实际上,任何真分数分
.该结论直到1880年才被英国数学家薛尔维斯特严格证明,实际上,任何真分数分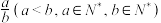 总可表示成
总可表示成 ①,这里
①,这里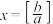 ,即不超过
,即不超过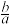 的最大整数,反复利用①式即可将
的最大整数,反复利用①式即可将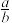 化为若干个“埃及分数”之和.请利用上面的方法将
化为若干个“埃及分数”之和.请利用上面的方法将 表示成3个互不相等的“埃及分数”之和,则
表示成3个互不相等的“埃及分数”之和,则
您最近半年使用:0次
7 . 我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,它体现了一种无限与有限的转化过程.比如在 表达式中“…”既代表无限次重复,但原式却又是个定值,它可以通过方程
表达式中“…”既代表无限次重复,但原式却又是个定值,它可以通过方程 解得
解得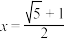 ,类比上述方法,则
,类比上述方法,则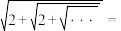 ( )
( )
 表达式中“…”既代表无限次重复,但原式却又是个定值,它可以通过方程
表达式中“…”既代表无限次重复,但原式却又是个定值,它可以通过方程 解得
解得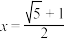 ,类比上述方法,则
,类比上述方法,则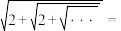 ( )
( )A.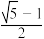 | B.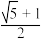 | C. | D. |
您最近半年使用:0次
2022-05-05更新
|
1331次组卷
|
3卷引用:四川省内江市2022届高三第三次模拟考试数学(文)试题
8 . 下列类比推理中,得到的结论正确的是( )
A.把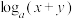 与 与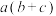 类比,则有 类比,则有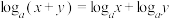 |
B.向量 , , 的数量积运算与实数 的数量积运算与实数 , , 的运算性质 的运算性质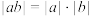 类比,则有 类比,则有 |
C.把 与 与 类比,则有 类比,则有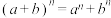 |
| D.把长方体与长方形类比,则有长方体的对角线平方等于长宽高的平方和 |
您最近半年使用:0次
9 . 给出下列三个类比结论:
① 与
与 类比,则有
类比,则有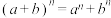 ;
;
②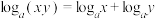 与
与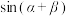 类比,则有
类比,则有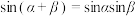 ;
;
③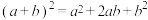 与
与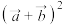 类比,则有
类比,则有 .
.
其中正确结论的个数是( )
①
 与
与 类比,则有
类比,则有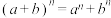 ;
;②
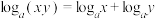 与
与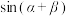 类比,则有
类比,则有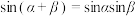 ;
;③
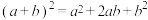 与
与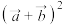 类比,则有
类比,则有 .
.其中正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
您最近半年使用:0次
2022-04-01更新
|
149次组卷
|
5卷引用:陕西省宝鸡市扶风县法门高中2018-2019学年高二下学期第一次月考数学(理)试题
名校
10 . 已知225的所有正约数之和可按如下方法得到:因为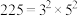 ,所以225的所有正约数之和为
,所以225的所有正约数之和为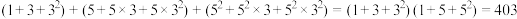 ,参照上述方法,可求得108的所有正约数之和为
,参照上述方法,可求得108的所有正约数之和为__________ .
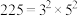 ,所以225的所有正约数之和为
,所以225的所有正约数之和为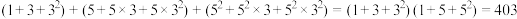 ,参照上述方法,可求得108的所有正约数之和为
,参照上述方法,可求得108的所有正约数之和为
您最近半年使用:0次
2022-03-15更新
|
160次组卷
|
2卷引用:安徽省“皖东县中联盟”2021-2022学年高三上学期期末联考文科数学试题



