阅读知识卡片,结合所学知识完成以下问题:
知识卡片1:
一般地,如果两数 在区间
在区间 上的图象连续不断,用分点
上的图象连续不断,用分点 将区间
将区间 等分成
等分成 个小区间,在每个小区间
个小区间,在每个小区间 上任取一点
上任取一点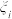 (
( ,2,…,n),作和式
,2,…,n),作和式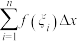
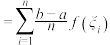 (其中
(其中 为小区间长度),当
为小区间长度),当 时,上述和式无限接近某个常数,这个常数叫做函数
时,上述和式无限接近某个常数,这个常数叫做函数 在区间
在区间 上的定积分,记作
上的定积分,记作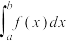 ,即
,即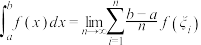 .这里,
.这里, 与
与 分别叫做积分下限与积分上限,区间
分别叫做积分下限与积分上限,区间 叫做积分区间,函数
叫做积分区间,函数 叫做被积函数,x叫做积分变量,
叫做被积函数,x叫做积分变量,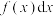 叫做被积式.从几何上看,如果在区间
叫做被积式.从几何上看,如果在区间 上函数
上函数 的图象连续不断且恒有
的图象连续不断且恒有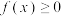 ,那么定积分
,那么定积分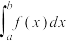 表示由直线
表示由直线 ,
, ,
, 和曲线
和曲线 所围成的区域(称为曲边梯形)的面积.
所围成的区域(称为曲边梯形)的面积.
知识卡片2:
一般地,如果 在区间
在区间 上的图象连续不断,并且
上的图象连续不断,并且 ,那么
,那么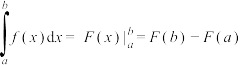 .这个结论叫做微积分基本定理,又叫做牛顿——莱布尼茨公式.例如,如图所示,对于函数
.这个结论叫做微积分基本定理,又叫做牛顿——莱布尼茨公式.例如,如图所示,对于函数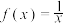 (
( ),从几何上看,定积分
),从几何上看,定积分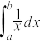 的值为由直线
的值为由直线 ,
, ,
, 和曲线
和曲线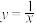 所围成的区域即曲边梯形
所围成的区域即曲边梯形 的面积,根据微积分基本定理可得
的面积,根据微积分基本定理可得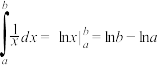 .
.
① ;
;
②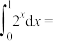 ;
;
③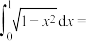 ;
;
④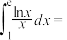 .
.
(2)已知 ,计算:
,计算:
①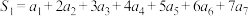 ;
;
②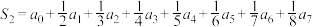
(3)当 ,
,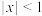 时,有如下表达式:
时,有如下表达式: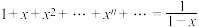 .计算:
.计算: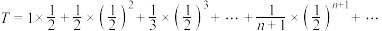
知识卡片1:
一般地,如果两数
 在区间
在区间 上的图象连续不断,用分点
上的图象连续不断,用分点 将区间
将区间 等分成
等分成 个小区间,在每个小区间
个小区间,在每个小区间 上任取一点
上任取一点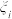 (
( ,2,…,n),作和式
,2,…,n),作和式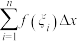
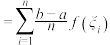 (其中
(其中 为小区间长度),当
为小区间长度),当 时,上述和式无限接近某个常数,这个常数叫做函数
时,上述和式无限接近某个常数,这个常数叫做函数 在区间
在区间 上的定积分,记作
上的定积分,记作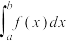 ,即
,即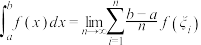 .这里,
.这里, 与
与 分别叫做积分下限与积分上限,区间
分别叫做积分下限与积分上限,区间 叫做积分区间,函数
叫做积分区间,函数 叫做被积函数,x叫做积分变量,
叫做被积函数,x叫做积分变量,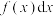 叫做被积式.从几何上看,如果在区间
叫做被积式.从几何上看,如果在区间 上函数
上函数 的图象连续不断且恒有
的图象连续不断且恒有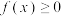 ,那么定积分
,那么定积分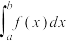 表示由直线
表示由直线 ,
, ,
, 和曲线
和曲线 所围成的区域(称为曲边梯形)的面积.
所围成的区域(称为曲边梯形)的面积.知识卡片2:
一般地,如果
 在区间
在区间 上的图象连续不断,并且
上的图象连续不断,并且 ,那么
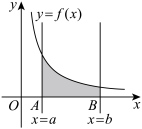
,那么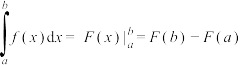 .这个结论叫做微积分基本定理,又叫做牛顿——莱布尼茨公式.例如,如图所示,对于函数
.这个结论叫做微积分基本定理,又叫做牛顿——莱布尼茨公式.例如,如图所示,对于函数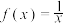 (
( ),从几何上看,定积分
),从几何上看,定积分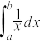 的值为由直线
的值为由直线 ,
, ,
, 和曲线
和曲线 所围成的区域即曲边梯形
所围成的区域即曲边梯形 的面积,根据微积分基本定理可得
的面积,根据微积分基本定理可得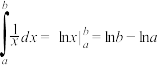 .
.
①
 ;
;②
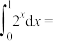 ;
;③
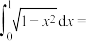 ;
;④
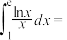 .
.(2)已知
 ,计算:
,计算:①
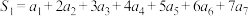 ;
;②
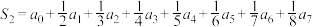
(3)当
 ,
,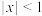 时,有如下表达式:
时,有如下表达式: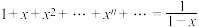 .计算:
.计算: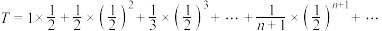
更新时间:2024-05-13 19:54:23
|
相似题推荐
解答题-证明题
|
困难
(0.15)
名校
解题方法
【推荐1】一般地,设函数 在区间[a,b]上连续,用分点
在区间[a,b]上连续,用分点 将区间[a,b]分成
将区间[a,b]分成 个小区间.每个小区间长度为
个小区间.每个小区间长度为 .在每个小区间
.在每个小区间 上任取一点
上任取一点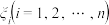 作和式
作和式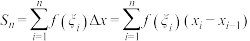 .如果
.如果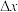 无限接近于0(亦即
无限接近于0(亦即 )时,上述和式
)时,上述和式 无限趋于常数
无限趋于常数 ,那么称该常数
,那么称该常数 为函数
为函数 在区间[a,b]上的定积分,记为
在区间[a,b]上的定积分,记为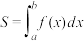 .当
.当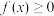 时,定积分
时,定积分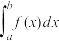 的几何意义表示由曲线
的几何意义表示由曲线 ,两条直线
,两条直线 与
与 轴所围成的曲边梯形的面积.如下图所示:
轴所围成的曲边梯形的面积.如下图所示: 是区间[a,b]上的连续函数,并且
是区间[a,b]上的连续函数,并且 ,那么
,那么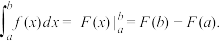
(1)求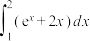 ;
;
(2)设函数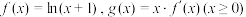 .
.
①若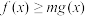 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
②数列 满足
满足 ,利用定积分的几何意义,证明:
,利用定积分的几何意义,证明: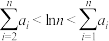 .
.
 在区间[a,b]上连续,用分点
在区间[a,b]上连续,用分点 将区间[a,b]分成
将区间[a,b]分成 个小区间.每个小区间长度为
个小区间.每个小区间长度为 .在每个小区间
.在每个小区间 上任取一点
上任取一点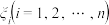 作和式
作和式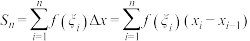 .如果
.如果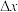 无限接近于0(亦即
无限接近于0(亦即 )时,上述和式
)时,上述和式 无限趋于常数
无限趋于常数 ,那么称该常数
,那么称该常数 为函数
为函数 在区间[a,b]上的定积分,记为
在区间[a,b]上的定积分,记为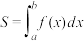 .当
.当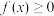 时,定积分
时,定积分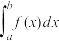 的几何意义表示由曲线
的几何意义表示由曲线 ,两条直线
,两条直线 与
与 轴所围成的曲边梯形的面积.如下图所示:
轴所围成的曲边梯形的面积.如下图所示: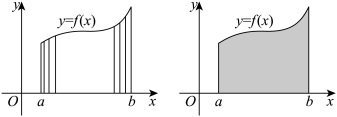
 是区间[a,b]上的连续函数,并且
是区间[a,b]上的连续函数,并且 ,那么
,那么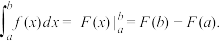
(1)求
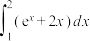 ;
;(2)设函数
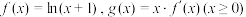 .
.①若
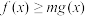 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;②数列
 满足
满足 ,利用定积分的几何意义,证明:
,利用定积分的几何意义,证明: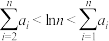 .
.
您最近一年使用:0次
解答题-问答题
|
困难
(0.15)
名校
解题方法
【推荐1】已知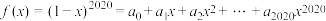 .
.
(1)求 的值;
的值;
(2)求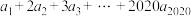 的值;
的值;
(3)求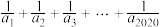 的值.
的值.
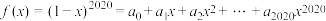 .
.(1)求
 的值;
的值;(2)求
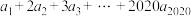 的值;
的值;(3)求
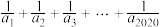 的值.
的值.
您最近一年使用:0次
解答题-证明题
|
困难
(0.15)
【推荐2】已知函数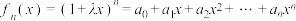 ,其中
,其中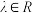 .
.
(1)若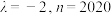 ,求
,求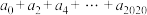 的值;
的值;
(2)若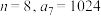 ,求
,求 的最大值;
的最大值;
(3)若 ,求证:
,求证: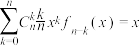 .
.
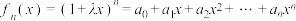 ,其中
,其中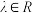 .
.(1)若
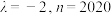 ,求
,求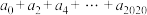 的值;
的值;(2)若
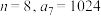 ,求
,求 的最大值;
的最大值;(3)若
 ,求证:
,求证: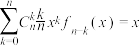 .
.
您最近一年使用:0次

 的导数
的导数 ,可记为
,可记为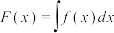 .若
.若 ,则
,则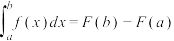 表示曲线
表示曲线 ,直线
,直线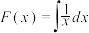 ,且
,且 ,求
,求 ,证明:
,证明: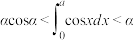 ,并解释其几何意义;
,并解释其几何意义;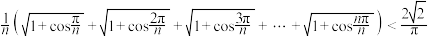 ,
, .
.
 元有序实数组
元有序实数组 为
为 为该向量的范数,已知
为该向量的范数,已知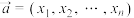 ,其中
,其中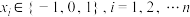 ,记范数为奇数的
,记范数为奇数的 的个数为
的个数为 ,这
,这 .
. 和
和 的值;
的值; 的值;
的值;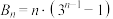 .
.


