解题方法
1 . (1)证明: 当 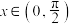 时,
时,  ;
;
(2)当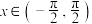 时,
时, 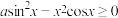 ,求
,求  的取值范围.
的取值范围.
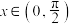 时,
时,  ;
;(2)当
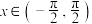 时,
时, 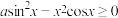 ,求
,求  的取值范围.
的取值范围.
您最近一年使用:0次
昨日更新
|
28次组卷
|
2卷引用:四川省成都市金堂县2024-2025学年高三上学期10月县联考数学试题
名校
2 . 已知函数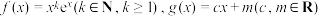 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(1)当 时,若曲线
时,若曲线 在
在 处的切线恰好是直线
处的切线恰好是直线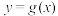 ,求
,求 和
和 的值;
的值;
(2)当 ,
, 时,关于
时,关于 的方程
的方程 有正实数根,求
有正实数根,求 的取值范围:
的取值范围:
(3)当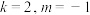 时,关于x的不等式
时,关于x的不等式 对于任意
对于任意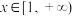 恒成立(其中
恒成立(其中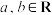 ),当
),当 取得最大值时,求
取得最大值时,求 的最小值.
的最小值.
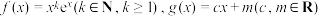 ,其中
,其中 是自然对数的底数.
是自然对数的底数.(1)当
 时,若曲线
时,若曲线 在
在 处的切线恰好是直线
处的切线恰好是直线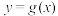 ,求
,求 和
和 的值;
的值;(2)当
 ,
, 时,关于
时,关于 的方程
的方程 有正实数根,求
有正实数根,求 的取值范围:
的取值范围:(3)当
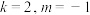 时,关于x的不等式
时,关于x的不等式 对于任意
对于任意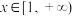 恒成立(其中
恒成立(其中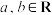 ),当
),当 取得最大值时,求
取得最大值时,求 的最小值.
的最小值.
您最近一年使用:0次
解题方法
3 . 已知函数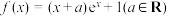 .
.
(1)若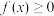 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)证明:当 时,
时,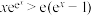 .
.
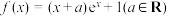 .
.(1)若
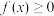 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)证明:当
 时,
时,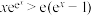 .
.
您最近一年使用:0次
名校
4 . 已知函数 .
.
(1)讨论 在区间
在区间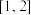 上的单调性;
上的单调性;
(2)若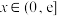 时,不等式
时,不等式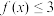 有解,求
有解,求 的取值范围.
的取值范围.
 .
.(1)讨论
 在区间
在区间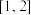 上的单调性;
上的单调性;(2)若
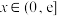 时,不等式
时,不等式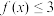 有解,求
有解,求 的取值范围.
的取值范围.
您最近一年使用:0次
昨日更新
|
540次组卷
|
2卷引用:甘肃省兰州市第七中学2024-2025学年高三上学期10月月考数学试题
名校
5 . 已知函数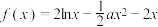 在
在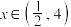 上存在单调递增区间,则实数a的取值范围为( )
上存在单调递增区间,则实数a的取值范围为( )
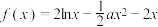 在
在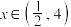 上存在单调递增区间,则实数a的取值范围为( )
上存在单调递增区间,则实数a的取值范围为( )A.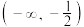 | B. |
C.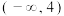 | D. |
您最近一年使用:0次
7日内更新
|
1042次组卷
|
2卷引用:重庆市第八中学校2024-2025学年高三上学期开学数学试题
名校
解题方法
6 . 已知 ,不等式
,不等式 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为______ .
 ,不等式
,不等式 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为
您最近一年使用:0次
名校
7 . 已知函数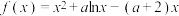 ,
,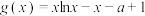 ,
, .
.
(1)讨论 的单调性;
的单调性;
(2)若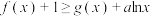 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
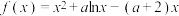 ,
,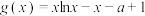 ,
, .
.(1)讨论
 的单调性;
的单调性;(2)若
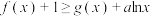 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
8 . 已知函数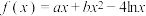 .
.
(1)若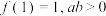 ,求
,求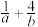 的最小值;
的最小值;
(2)当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
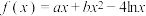 .
.(1)若
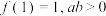 ,求
,求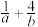 的最小值;
的最小值;(2)当
 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 已知函数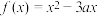 ,
,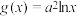 .
.
(1)若函数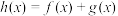 在
在 处取得极大值,求
处取得极大值,求 的极值及单调区间;
的极值及单调区间;
(2)若 ,不等式
,不等式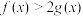 对一切
对一切 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
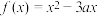 ,
,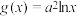 .
.(1)若函数
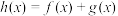 在
在 处取得极大值,求
处取得极大值,求 的极值及单调区间;
的极值及单调区间;(2)若
 ,不等式
,不等式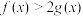 对一切
对一切 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
7日内更新
|
819次组卷
|
2卷引用:重庆市巴蜀中学校2024-2025学年高三上学期9月月考数学试题
名校
10 . 已知 ,函数
,函数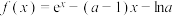 .
.
(1)讨论 的单调性;
的单调性;
(2)若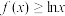 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 ,函数
,函数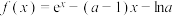 .
.(1)讨论
 的单调性;
的单调性;(2)若
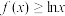 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
570次组卷
|
4卷引用:广东省肇庆市2024-2025学年高三上学期9月联考数学试题



