名校
1 . 已知函数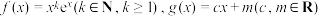 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(1)当 时,若曲线
时,若曲线 在
在 处的切线恰好是直线
处的切线恰好是直线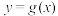 ,求
,求 和
和 的值;
的值;
(2)当 ,
, 时,关于
时,关于 的方程
的方程 有正实数根,求
有正实数根,求 的取值范围:
的取值范围:
(3)当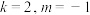 时,关于x的不等式
时,关于x的不等式 对于任意
对于任意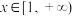 恒成立(其中
恒成立(其中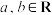 ),当
),当 取得最大值时,求
取得最大值时,求 的最小值.
的最小值.
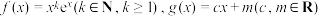 ,其中
,其中 是自然对数的底数.
是自然对数的底数.(1)当
 时,若曲线
时,若曲线 在
在 处的切线恰好是直线
处的切线恰好是直线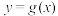 ,求
,求 和
和 的值;
的值;(2)当
 ,
, 时,关于
时,关于 的方程
的方程 有正实数根,求
有正实数根,求 的取值范围:
的取值范围:(3)当
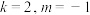 时,关于x的不等式
时,关于x的不等式 对于任意
对于任意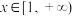 恒成立(其中
恒成立(其中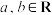 ),当
),当 取得最大值时,求
取得最大值时,求 的最小值.
的最小值.
您最近一年使用:0次
解题方法
2 . 已知不等式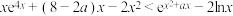 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围为
的取值范围为______ .
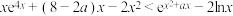 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围为
的取值范围为
您最近一年使用:0次
解题方法
3 . 已知函数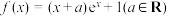 .
.
(1)若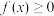 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)证明:当 时,
时,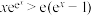 .
.
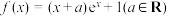 .
.(1)若
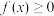 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)证明:当
 时,
时,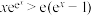 .
.
您最近一年使用:0次
名校
解题方法
4 . 已知函数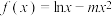 ,
,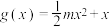 ,
, ,令
,令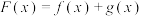 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若关于x的不等式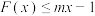 恒成立,求整数m的最小值.
恒成立,求整数m的最小值.
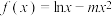 ,
,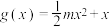 ,
, ,令
,令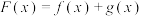 .
.(1)讨论函数
 的单调性;
的单调性;(2)若关于x的不等式
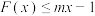 恒成立,求整数m的最小值.
恒成立,求整数m的最小值.
您最近一年使用:0次
昨日更新
|
498次组卷
|
3卷引用:福建省龙岩市第四中学2023-2024学年高三上学期第一次质量检测数学试题
福建省龙岩市第四中学2023-2024学年高三上学期第一次质量检测数学试题(已下线)考点26 导数的应用--不等式问题 --高考数学100个黄金考点(2025届)【练】内蒙古自治区赤峰市红山区赤峰二中2024-2025学年高三上学期10月月考数学试题
5 . 设函数 .
.
(1)若 在
在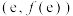 处的切线方程为
处的切线方程为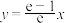 ,求实数
,求实数 的取值;
的取值;
(2)试讨论 的单调性;
的单调性;
(3)对任意的 ,恒有
,恒有 成立,求实数a的取值范围.
成立,求实数a的取值范围.
 .
.(1)若
 在
在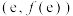 处的切线方程为
处的切线方程为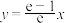 ,求实数
,求实数 的取值;
的取值;(2)试讨论
 的单调性;
的单调性;(3)对任意的
 ,恒有
,恒有 成立,求实数a的取值范围.
成立,求实数a的取值范围.
您最近一年使用:0次
名校
6 . 设函数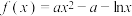 ,
,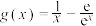 ,其中
,其中 ,
,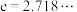 为自然对数的底数.
为自然对数的底数.
(1)讨论 的单调性;
的单调性;
(2)证明:当 时,
时,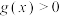 ;
;
(3)确定 的所有可能取值,使得
的所有可能取值,使得 在区间
在区间 内恒成立.
内恒成立.
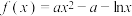 ,
,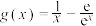 ,其中
,其中 ,
,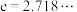 为自然对数的底数.
为自然对数的底数.(1)讨论
 的单调性;
的单调性;(2)证明:当
 时,
时,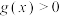 ;
;(3)确定
 的所有可能取值,使得
的所有可能取值,使得 在区间
在区间 内恒成立.
内恒成立.
您最近一年使用:0次
7 . 已知函数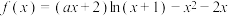 .
.
(1)当 时,求
时,求 的单调区间与极值;
的单调区间与极值;
(2)当 时,
时, 恒成立,求a的取值范围.
恒成立,求a的取值范围.
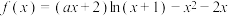 .
.(1)当
 时,求
时,求 的单调区间与极值;
的单调区间与极值;(2)当
 时,
时, 恒成立,求a的取值范围.
恒成立,求a的取值范围.
您最近一年使用:0次
昨日更新
|
429次组卷
|
2卷引用:河南省创新发展联盟2024-2025学年高三上学期9月月考数学试题
名校
解题方法
8 . 已知函数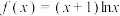 ,
,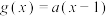 .
.
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 对任意的
对任意的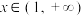 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若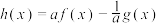 有三个零点
有三个零点 ,
, ,
, ,且
,且 ,求证:
,求证: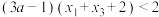 .
.
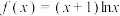 ,
,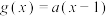 .
.(1)求曲线
 在
在 处的切线方程;
处的切线方程;(2)若
 对任意的
对任意的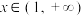 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
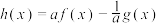 有三个零点
有三个零点 ,
, ,
, ,且
,且 ,求证:
,求证: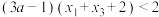 .
.
您最近一年使用:0次
7日内更新
|
250次组卷
|
3卷引用:天津市第四十七中学2024-2025学年高三上学期10月月考数学试题
名校
解题方法
9 . 已知 ,不等式
,不等式 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为______ .
 ,不等式
,不等式 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为
您最近一年使用:0次
名校
解题方法
10 . 已知函数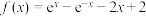 .(
.(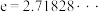 )
)
(1)判断函数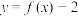 的奇偶性并证明,据此说明
的奇偶性并证明,据此说明 图象的对称性;
图象的对称性;
(2)若任意 ,
, ,求实数m的取值范围.
,求实数m的取值范围.
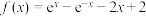 .(
.(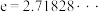 )
)(1)判断函数
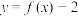 的奇偶性并证明,据此说明
的奇偶性并证明,据此说明 图象的对称性;
图象的对称性;(2)若任意
 ,
, ,求实数m的取值范围.
,求实数m的取值范围.
您最近一年使用:0次
7日内更新
|
752次组卷
|
2卷引用:江苏省海门中学2025届高三上学期第一次调研考试数学试题



