1 . 曲线 在
在 处的切线方程为
处的切线方程为______ .
 在
在 处的切线方程为
处的切线方程为
您最近一年使用:0次
解题方法
2 . 已知曲线 :
: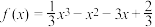 .
.
(1)求 在点
在点 处的切线方程;
处的切线方程;
(2)求 的极值.
的极值.
 :
: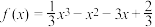 .
.(1)求
 在点
在点 处的切线方程;
处的切线方程;(2)求
 的极值.
的极值.
您最近一年使用:0次
2024高二下·全国·专题练习
3 . 设函数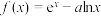 .
.
(1)当 ,求
,求 在点
在点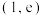 处的切线方程;
处的切线方程;
(2)证明:当 时,
时,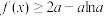 ;
;
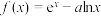 .
.(1)当
 ,求
,求 在点
在点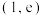 处的切线方程;
处的切线方程;(2)证明:当
 时,
时,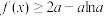 ;
;
您最近一年使用:0次
昨日更新
|
259次组卷
|
3卷引用:专题4 利用导数解决不等式证明问题【练】(高二期末压轴专项)
(已下线)专题4 利用导数解决不等式证明问题【练】(高二期末压轴专项)湖南省益阳市安化县两校联考2023-2024学年高二下学期7月期末自检数学试题湖南省永州市名校联盟2023-2024学年高二下学期期末考试数学试题
4 . 已知函数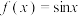 ,
,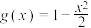 .
.
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)证明:对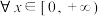 ,
, 恒成立(
恒成立( 为
为 的导数);
的导数);
(3)设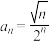 ,证明:
,证明: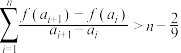 (
( ).
).
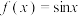 ,
,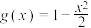 .
.(1)求曲线
 在
在 处的切线方程;
处的切线方程;(2)证明:对
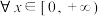 ,
, 恒成立(
恒成立( 为
为 的导数);
的导数);(3)设
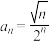 ,证明:
,证明: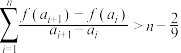 (
( ).
).
您最近一年使用:0次
5 . 已知函数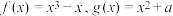 ,曲线
,曲线 在点
在点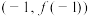 处的切线也是曲线
处的切线也是曲线 的切线.则a的值是
的切线.则a的值是__________
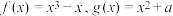 ,曲线
,曲线 在点
在点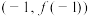 处的切线也是曲线
处的切线也是曲线 的切线.则a的值是
的切线.则a的值是
您最近一年使用:0次
解题方法
6 . 设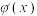 为函数
为函数 的导函数,若
的导函数,若 为函数
为函数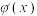 的极值点,则
的极值点,则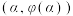 为曲线
为曲线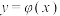 的拐点,亦称函数
的拐点,亦称函数 的拐点.已知函数
的拐点.已知函数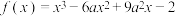 .
.
(1)当 时,求曲线
时,求曲线 在点
在点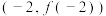 处的切线方程;
处的切线方程;
(2)求函数 的极值;
的极值;
(3)当 时,证明:函数
时,证明:函数 的两个极值和拐点纵坐标可构成等差数列.
的两个极值和拐点纵坐标可构成等差数列.
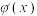 为函数
为函数 的导函数,若
的导函数,若 为函数
为函数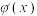 的极值点,则
的极值点,则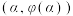 为曲线
为曲线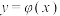 的拐点,亦称函数
的拐点,亦称函数 的拐点.已知函数
的拐点.已知函数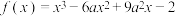 .
.(1)当
 时,求曲线
时,求曲线 在点
在点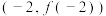 处的切线方程;
处的切线方程;(2)求函数
 的极值;
的极值;(3)当
 时,证明:函数
时,证明:函数 的两个极值和拐点纵坐标可构成等差数列.
的两个极值和拐点纵坐标可构成等差数列.
您最近一年使用:0次
7 . 已知函数 .
.
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若关于 的不等式
的不等式 恒成立,证明:
恒成立,证明: 且
且 .
.
 .
.(1)求曲线
 在点
在点 处的切线方程;
处的切线方程;(2)若关于
 的不等式
的不等式 恒成立,证明:
恒成立,证明: 且
且 .
.
您最近一年使用:0次
8 . 已知函数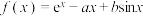 .
.
(1)若 ,求曲线
,求曲线 在点
在点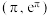 处的切线的斜率;
处的切线的斜率;
(2)若 ,讨论
,讨论 的单调性;
的单调性;
(3)若 ,且
,且 时,
时,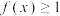 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
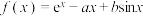 .
.(1)若
 ,求曲线
,求曲线 在点
在点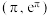 处的切线的斜率;
处的切线的斜率;(2)若
 ,讨论
,讨论 的单调性;
的单调性;(3)若
 ,且
,且 时,
时,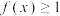 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
9 . 已知函数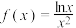 ,则( )
,则( )
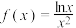 ,则( )
,则( )A. 的极大值点为 的极大值点为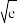 | B. 的极大值为 的极大值为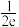 |
C. 有两个零点 有两个零点 | D.直线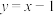 是曲线 是曲线 的一条切线 的一条切线 |
您最近一年使用:0次
10 . 函数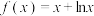 在
在 处的切线的斜率为
处的切线的斜率为__________ .
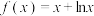 在
在 处的切线的斜率为
处的切线的斜率为
您最近一年使用:0次



