解题方法
1 . 已知函数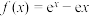 的极值点为a,则
的极值点为a,则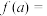 ( )
( )
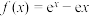 的极值点为a,则
的极值点为a,则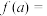 ( )
( )A. | B.0 | C.1 | D.2 |
您最近半年使用:0次
昨日更新
|
160次组卷
|
3卷引用:青海省部分学校2023-2024学年高三下学期联考模拟预测理科数学试题
青海省部分学校2023-2024学年高三下学期联考模拟预测理科数学试题青海省部分学校2023-2024学年高三下学期联考模拟预测文科数学试题(已下线)模块五 专题2 全真基础模拟2(苏教版高二期中研习)
2 . 函数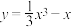 的驻点为
的驻点为____________ .
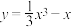 的驻点为
的驻点为
您最近半年使用:0次
名校
3 . 下列关于三次函数 叙述正确的是( )
叙述正确的是( )
 叙述正确的是( )
叙述正确的是( )A.函数 的图象一定是中心对称图形 的图象一定是中心对称图形 |
B.函数 可能只有一个极值点 可能只有一个极值点 |
C.当 时, 时, 在 在 处的切线与函数 处的切线与函数 的图象有且仅有两个交点 的图象有且仅有两个交点 |
D.当 时,则过点 时,则过点 的切线可能有一条或者三条 的切线可能有一条或者三条 |
您最近半年使用:0次
名校
4 . 关于函数 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )A. 是 是 的极大值点 的极大值点 |
B.函数 有且只有1个零点 有且只有1个零点 |
C.存在正整数k,使得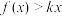 恒成立 恒成立 |
D.对任意两个正实数 ,且 ,且 ,若 ,若 ,则 ,则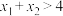 |
您最近半年使用:0次
名校
解题方法
5 . 设函数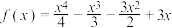 ,则( )
,则( )
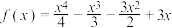 ,则( )
,则( )A. 有 有 个极大值点 个极大值点 |
B. 有 有 个极小值点 个极小值点 |
C. 是 是 的极大值点 的极大值点 |
D.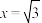 是 是 的极小值点 的极小值点 |
您最近半年使用:0次
名校
6 . 已知函数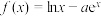 ,曲线
,曲线 在点
在点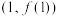 处切线斜率为
处切线斜率为
(1)求 的值;
的值;
(2)求证: 有且只有一个极值点;
有且只有一个极值点;
(3)求证:方程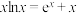 无解.
无解.
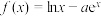 ,曲线
,曲线 在点
在点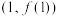 处切线斜率为
处切线斜率为
(1)求
 的值;
的值;(2)求证:
 有且只有一个极值点;
有且只有一个极值点;(3)求证:方程
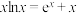 无解.
无解.
您最近半年使用:0次
7 . 已知函数 ,给出下列四个结论:
,给出下列四个结论:
①当 时,对任意
时,对任意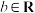 ,
, 有1个极值点;
有1个极值点;
②当 时,存在
时,存在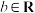 ,使得
,使得 存在极值点;
存在极值点;
③当 时,对任意
时,对任意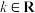 ,
, 有一个零点;
有一个零点;
④当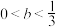 时,存在
时,存在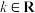 ,使得
,使得 有3个零点.
有3个零点.
其中所有正确结论的序号是______ .
 ,给出下列四个结论:
,给出下列四个结论:①当
 时,对任意
时,对任意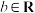 ,
, 有1个极值点;
有1个极值点;②当
 时,存在
时,存在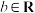 ,使得
,使得 存在极值点;
存在极值点;③当
 时,对任意
时,对任意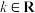 ,
, 有一个零点;
有一个零点;④当
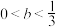 时,存在
时,存在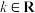 ,使得
,使得 有3个零点.
有3个零点.其中所有正确结论的序号是
您最近半年使用:0次
解题方法
8 . 已知双曲线 的左,右顶点分别为
的左,右顶点分别为 是双曲线上不同于
是双曲线上不同于 ,
, 的一点,设直线
的一点,设直线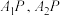 的斜率分别为
的斜率分别为 ,则当
,则当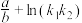 取得最小值时,双曲线
取得最小值时,双曲线 的离心率为( )
的离心率为( )
 的左,右顶点分别为
的左,右顶点分别为 是双曲线上不同于
是双曲线上不同于 ,
, 的一点,设直线
的一点,设直线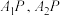 的斜率分别为
的斜率分别为 ,则当
,则当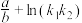 取得最小值时,双曲线
取得最小值时,双曲线 的离心率为( )
的离心率为( )A.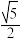 | B. | C. | D.2 |
您最近半年使用:0次
名校
9 . 已知 是定义在
是定义在 上连续的奇函数,其导函数为
上连续的奇函数,其导函数为 ,
,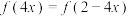 ,当
,当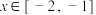 时,
时,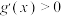 ,则( )
,则( )
 是定义在
是定义在 上连续的奇函数,其导函数为
上连续的奇函数,其导函数为 ,
,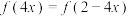 ,当
,当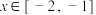 时,
时,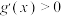 ,则( )
,则( )A. 为偶函数 为偶函数 | B. 的图象关于直线 的图象关于直线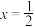 对称 对称 |
C.4为 的周期 的周期 | D. 在 在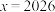 处取得极小值 处取得极小值 |
您最近半年使用:0次
7日内更新
|
323次组卷
|
2卷引用:江西省贵溪市实验中学2024届高三下学期高考仿真模拟(一)(3月)数学试卷
10 . 已知函数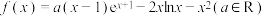 .
.
(1)当 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;
(2)讨论函数 的极值点个数.
的极值点个数.
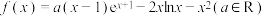 .
.(1)当
 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;(2)讨论函数
 的极值点个数.
的极值点个数.
您最近半年使用:0次



