解题方法
1 . 已知小张每天早上在7:00∼8:00中的任一时刻随机出门上班,他订购的报纸每天在7:30∼8:10中的任一时刻随机送到,则小张在出门时能拿到报纸的概率为( )
A. | B.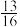 | C.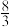 | D.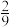 |
您最近半年使用:0次
名校
解题方法
2 . 甲先生接到某快递公司快递员乙的电话通知,约定于下午2点~3点之间到某小区便利店门口签收货物.由于甲先生从写字楼出来的时间不确定,快递员乙也在边送其他快递边往约定地点赶,两人约定到达后需要等待对方20分钟,假设两人都在下午2点~3点之间的任意时刻到达约定地点,不考虑其他因素的影响,则甲先生能签收到货物的概率是______ .
您最近半年使用:0次
解题方法
3 . 已知关于 的不等式组
的不等式组 表示的平面区域为
表示的平面区域为 ,在区域
,在区域 内随机取一点
内随机取一点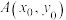 ,则满足
,则满足 的概率为( )
的概率为( )
A.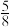 | B. | C. | D. |
您最近半年使用:0次
2024-03-23更新
|
217次组卷
|
2卷引用:陕西省2024届高三下学期2月大联考数学试题(全国乙卷)
名校
解题方法
4 . 已知平面直角坐标系内的动点 满足
满足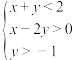 ,则P满足
,则P满足 的概率为( )
的概率为( )
 满足
满足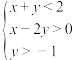 ,则P满足
,则P满足 的概率为( )
的概率为( )A.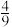 | B.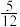 | C.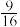 | D.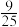 |
您最近半年使用:0次
2023-12-21更新
|
200次组卷
|
2卷引用:陕西省榆林市十校2024届高三上学期12月联考数学(文)试题
名校
解题方法
5 . 在区间 和
和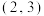 中各随机取1个数
中各随机取1个数 和
和 ,则用几何概型可求得
,则用几何概型可求得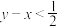 的概率为( )
的概率为( )
 和
和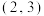 中各随机取1个数
中各随机取1个数 和
和 ,则用几何概型可求得
,则用几何概型可求得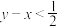 的概率为( )
的概率为( )A.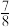 | B. | C. | D. |
您最近半年使用:0次
2023-09-01更新
|
219次组卷
|
2卷引用:内蒙古包头市2023-2024学年高三上学期调研考试理科数学试题
名校
解题方法
6 . 某人每天早上在 任一时刻随机出门上班,他的报纸每天在
任一时刻随机出门上班,他的报纸每天在 任一时刻随机送到,则该人在出门时能拿到报纸的概率为( )
任一时刻随机送到,则该人在出门时能拿到报纸的概率为( )
 任一时刻随机出门上班,他的报纸每天在
任一时刻随机出门上班,他的报纸每天在 任一时刻随机送到,则该人在出门时能拿到报纸的概率为( )
任一时刻随机送到,则该人在出门时能拿到报纸的概率为( )A. | B. | C. | D.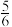 |
您最近半年使用:0次
2023-06-03更新
|
708次组卷
|
2卷引用:四川省成都市树德中学2023届高三适应性考试文科数学试题
解题方法
7 . 在区间 内任取两个实数a,b,则
内任取两个实数a,b,则 的概率为( ).
的概率为( ).
 内任取两个实数a,b,则
内任取两个实数a,b,则 的概率为( ).
的概率为( ).A. | B. | C. | D. |
您最近半年使用:0次
2023-05-13更新
|
526次组卷
|
3卷引用:四川省凉山彝族自治州2023届高三第三次诊断性检测数学(文)试题
名校
解题方法
8 . 长为6的线段.
(1)在线段上任取一点将线段分成两段,要求两段的长度均为整数,求两段长度不相等的概率;
(2)在线段上任取两点将线段分成三段,求三段构成三角形的概率.
(1)在线段上任取一点将线段分成两段,要求两段的长度均为整数,求两段长度不相等的概率;
(2)在线段上任取两点将线段分成三段,求三段构成三角形的概率.
您最近半年使用:0次
解题方法
9 . 在一个圆上随机取三点,则以这三点为顶点的三角形是锐角三角形的概率为( )
A. | B. | C. | D. |
您最近半年使用:0次
2023-03-07更新
|
313次组卷
|
4卷引用:新疆维吾尔自治区普通高考2023届高三第一次适应性检测数学(理)试题
名校
解题方法
10 . 小明和小强计划去博物馆参观,约定上午9:00~9:30之间的任何一个时间在博物馆会合.两人商量好提前到达博物馆的人最多等待对方10分钟,如果对方10分钟内没到,那么等待的人先进去参观,则两人能够在博物馆门口会合的概率是______ .
您最近半年使用:0次
2023-03-03更新
|
497次组卷
|
2卷引用:四川省成都石室中学2022-2023学年高三下学期入学考试文科数学试题



