1 . 对任意正整数n,记集合 ,
, .
.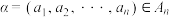 ,
,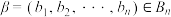 ,若对任意
,若对任意 都有
都有 ,则记
,则记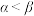 .
.
(1)写出集合 和
和 ;
;
(2)证明:对任意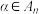 ,存在
,存在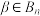 ,使得
,使得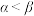 ;
;
(3)设集合 .求证:
.求证: 中的元素个数是完全平方数.
中的元素个数是完全平方数.
 ,
, .
.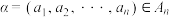 ,
,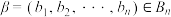 ,若对任意
,若对任意 都有
都有 ,则记
,则记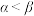 .
.(1)写出集合
 和
和 ;
;(2)证明:对任意
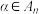 ,存在
,存在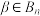 ,使得
,使得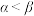 ;
;(3)设集合
 .求证:
.求证: 中的元素个数是完全平方数.
中的元素个数是完全平方数.
您最近一年使用:0次
2023-11-15更新
|
158次组卷
|
4卷引用:北京市朝阳区2022届高三上学期期末统一检测数学试题
名校
2 . 设A为非空集合,令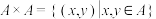 ,则
,则 的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如
的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如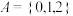 时,
时,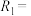 {0,2},
{0,2},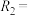
 ,
, ,
,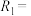 {(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:
{(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:
①(自反性)若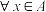 ,有
,有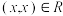 ,则称R在A上是自反的;
,则称R在A上是自反的;
②(对称性)若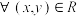 ,有
,有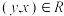 ,则称R在A上是对称的;
,则称R在A上是对称的;
③(传递性)若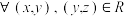 ,有
,有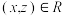 ,则称R在A上是传递的;
,则称R在A上是传递的;
如果R同时满足这3条性质,则称R为A上的等价关系.
(1)已知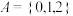 ,按要求填空:
,按要求填空:
①用列举法写出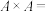 ______________________;
______________________;
②A上的关系有____________个(用数值做答);
③用列举法写出A上的所有等价关系:{(0,0),(1,1),(2,2)},{(0,0),(1,1),(2,2),(0,1),(1,0)},{(0,0),(1,1),(2,2),(0,2),(2,0)},_______________,_______________,共5个.
(2)设 和
和 是某个非空集合A上的关系,证明:
是某个非空集合A上的关系,证明:
①若 ,
, 是自反的和对称的,则
是自反的和对称的,则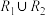 也是自反的和对称的;
也是自反的和对称的;
②若 ,
, 是传递的,则
是传递的,则 也是传递的.
也是传递的.
(3)若给定的集合A有n个元素( ),
), ,
, ,...,
,..., 为A的非空子集,满足
为A的非空子集,满足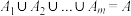 且两两交集为空集.求证:
且两两交集为空集.求证: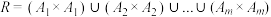 为A上的等价关系.
为A上的等价关系.
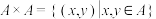 ,则
,则 的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如
的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如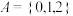 时,
时,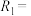 {0,2},
{0,2},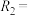
 ,
, ,
,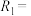 {(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:
{(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:①(自反性)若
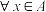 ,有
,有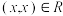 ,则称R在A上是自反的;
,则称R在A上是自反的;②(对称性)若
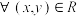 ,有
,有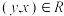 ,则称R在A上是对称的;
,则称R在A上是对称的;③(传递性)若
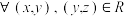 ,有
,有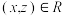 ,则称R在A上是传递的;
,则称R在A上是传递的;如果R同时满足这3条性质,则称R为A上的等价关系.
(1)已知
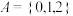 ,按要求填空:
,按要求填空:①用列举法写出
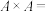 ______________________;
______________________;②A上的关系有____________个(用数值做答);
③用列举法写出A上的所有等价关系:{(0,0),(1,1),(2,2)},{(0,0),(1,1),(2,2),(0,1),(1,0)},{(0,0),(1,1),(2,2),(0,2),(2,0)},_______________,_______________,共5个.
(2)设
 和
和 是某个非空集合A上的关系,证明:
是某个非空集合A上的关系,证明:①若
 ,
, 是自反的和对称的,则
是自反的和对称的,则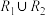 也是自反的和对称的;
也是自反的和对称的;②若
 ,
, 是传递的,则
是传递的,则 也是传递的.
也是传递的.(3)若给定的集合A有n个元素(
 ),
), ,
, ,...,
,..., 为A的非空子集,满足
为A的非空子集,满足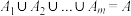 且两两交集为空集.求证:
且两两交集为空集.求证: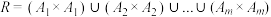 为A上的等价关系.
为A上的等价关系.
您最近一年使用:0次
名校
3 . 对于正整数集合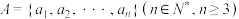 ,如果任意去掉其中一个元素
,如果任意去掉其中一个元素 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合 为“可分集合”.
为“可分集合”.
(1)判断集合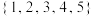 和
和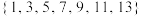 是否是“可分集合”(不必写过程);
是否是“可分集合”(不必写过程);
(2)求证:五个元素的集合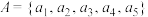 一定不是“可分集合”;
一定不是“可分集合”;
(3)若集合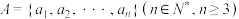 是“可分集合”.
是“可分集合”.
①证明: 为奇数;
为奇数;
②求集合 中元素个数的最小值.
中元素个数的最小值.
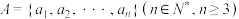 ,如果任意去掉其中一个元素
,如果任意去掉其中一个元素 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合 为“可分集合”.
为“可分集合”.(1)判断集合
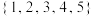 和
和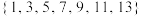 是否是“可分集合”(不必写过程);
是否是“可分集合”(不必写过程);(2)求证:五个元素的集合
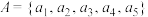 一定不是“可分集合”;
一定不是“可分集合”;(3)若集合
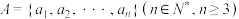 是“可分集合”.
是“可分集合”.①证明:
 为奇数;
为奇数;②求集合
 中元素个数的最小值.
中元素个数的最小值.
您最近一年使用:0次
2019-12-27更新
|
574次组卷
|
4卷引用:北京市密云区2019-2020学年高一上学期期末数学试题
北京市密云区2019-2020学年高一上学期期末数学试题北京市顺义区牛栏山第一中学2019-2020学年高三上学期期中数学试题(已下线)第1章《集合》 培优测试卷(二)-2021-2022学年高一数学上册同步培优训练系列(苏教版2019)(已下线)专题05 集合与常用逻辑用语压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)
4 . 已知集合A为非空数集.定义:
(1)若集合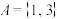 ,直接写出集合S,T;
,直接写出集合S,T;
(2)若集合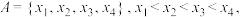 且
且 .求证:
.求证: ;
;
(3)若集合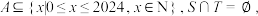 记
记 为集合A中元素的个数,求
为集合A中元素的个数,求 的最大值.
的最大值.

(1)若集合
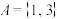 ,直接写出集合S,T;
,直接写出集合S,T;(2)若集合
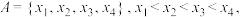 且
且 .求证:
.求证: ;
;(3)若集合
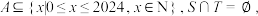 记
记 为集合A中元素的个数,求
为集合A中元素的个数,求 的最大值.
的最大值.
您最近一年使用:0次
名校
5 . 设正整数 ,若由实数组成的集合
,若由实数组成的集合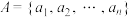 满足如下性质,则称
满足如下性质,则称 为
为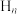 集合:对
集合:对 中任意四个不同的元素
中任意四个不同的元素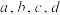 ,均有
,均有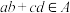 .
.
(1)判断集合 和
和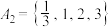 是否为
是否为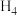 集合,说明理由;
集合,说明理由;
(2)若集合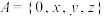 为
为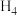 集合,求
集合,求 中大于1的元素的可能个数;
中大于1的元素的可能个数;
(3)若集合 为
为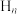 集合,求证:
集合,求证: 中元素不能全为正实数.
中元素不能全为正实数.
 ,若由实数组成的集合
,若由实数组成的集合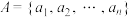 满足如下性质,则称
满足如下性质,则称 为
为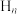 集合:对
集合:对 中任意四个不同的元素
中任意四个不同的元素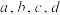 ,均有
,均有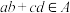 .
.(1)判断集合
 和
和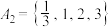 是否为
是否为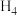 集合,说明理由;
集合,说明理由;(2)若集合
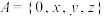 为
为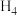 集合,求
集合,求 中大于1的元素的可能个数;
中大于1的元素的可能个数;(3)若集合
 为
为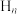 集合,求证:
集合,求证: 中元素不能全为正实数.
中元素不能全为正实数.
您最近一年使用:0次
2024-01-19更新
|
211次组卷
|
2卷引用:北京市朝阳区2023-2024学年高二上学期期末质量检测数学试题
名校
6 . 已知 是各项均为正整数的无穷递增数列,对于
是各项均为正整数的无穷递增数列,对于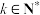 ,定义集合
,定义集合 ,设
,设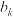 为集合
为集合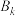 中的元素个数,若
中的元素个数,若 时,规定
时,规定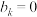 .
.
(1)若 ,写出
,写出 及
及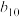 的值;
的值;
(2)若数列 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(3)设集合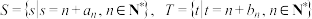 ,求证:
,求证: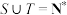 且
且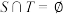 .
.
 是各项均为正整数的无穷递增数列,对于
是各项均为正整数的无穷递增数列,对于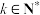 ,定义集合
,定义集合 ,设
,设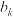 为集合
为集合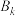 中的元素个数,若
中的元素个数,若 时,规定
时,规定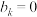 .
.(1)若
 ,写出
,写出 及
及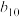 的值;
的值;(2)若数列
 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;(3)设集合
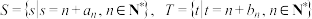 ,求证:
,求证: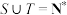 且
且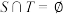 .
.
您最近一年使用:0次
2024-01-21更新
|
1345次组卷
|
7卷引用:北京市朝阳区2024届高三上学期期末数学试题
北京市朝阳区2024届高三上学期期末数学试题(已下线)专题1 集合新定义题(九省联考第19题模式)讲(已下线)2024年高考数学二轮复习测试卷(北京专用)(已下线)黄金卷01(2024新题型)(已下线)微考点4-1 新高考新试卷结构压轴题新定义数列试题分类汇编广东省江门市开平市忠源纪念中学2024届高三下学期高考冲刺考试(一)数学试卷江苏省常州市华罗庚中学2024届高三下学期4月二模训练数学试卷
名校
7 . 已知数列A:a1,a2,…,aN 的各项均为正整数,设集合
的各项均为正整数,设集合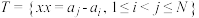 ,记T的元素个数为
,记T的元素个数为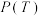 .
.
(1)①若数列A:1,2,4,5,求集合T,并写出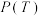 的值;
的值;
②若数列A:1,3,x,y,且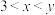 ,
, ,求数列A和集合T;
,求数列A和集合T;
(2)若A是递增数列,求证:“ ”的充要条件是“A为等差数列”;
”的充要条件是“A为等差数列”;
(3)请你判断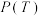 是否存在最大值,并说明理由.
是否存在最大值,并说明理由.
 的各项均为正整数,设集合
的各项均为正整数,设集合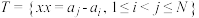 ,记T的元素个数为
,记T的元素个数为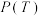 .
.(1)①若数列A:1,2,4,5,求集合T,并写出
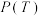 的值;
的值;②若数列A:1,3,x,y,且
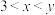 ,
, ,求数列A和集合T;
,求数列A和集合T;(2)若A是递增数列,求证:“
 ”的充要条件是“A为等差数列”;
”的充要条件是“A为等差数列”;(3)请你判断
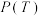 是否存在最大值,并说明理由.
是否存在最大值,并说明理由.
您最近一年使用:0次
2023-12-30更新
|
715次组卷
|
7卷引用:北京市第二十四中学2023-2024学年高二上学期期末数学模拟试卷
北京市第二十四中学2023-2024学年高二上学期期末数学模拟试卷北京市北京大学附属中学2021-2022学年高二上学期期中数学试题(已下线)北京市海淀区2023届高三上学期期末练习数学试题变式题16-21(已下线)专题03 条件存在型【讲】【北京版】1广东省惠州市第一中学2024届高三元月阶段测试数学试题(已下线)专题1 集合新定义题(九省联考第19题模式)练(已下线)高考数学冲刺押题卷01(2024新题型)
8 . 对于正整数集合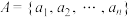 (
(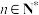 ,
, )如果去掉其中任意一个元素.
)如果去掉其中任意一个元素.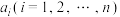 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合 为“和谐集”.
为“和谐集”.
(1)判断集合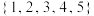 是否是“和谐集”,并说明理由;
是否是“和谐集”,并说明理由;
(2)求证:若集合 是“和谐集”.则集合
是“和谐集”.则集合 中元素个数为奇数;
中元素个数为奇数;
(3)若集合 是“和谐集”,求集合
是“和谐集”,求集合 中元素个数的最小值.
中元素个数的最小值.
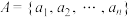 (
(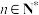 ,
, )如果去掉其中任意一个元素.
)如果去掉其中任意一个元素.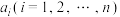 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合 为“和谐集”.
为“和谐集”.(1)判断集合
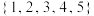 是否是“和谐集”,并说明理由;
是否是“和谐集”,并说明理由;(2)求证:若集合
 是“和谐集”.则集合
是“和谐集”.则集合 中元素个数为奇数;
中元素个数为奇数;(3)若集合
 是“和谐集”,求集合
是“和谐集”,求集合 中元素个数的最小值.
中元素个数的最小值.
您最近一年使用:0次
名校
解题方法
9 . 设 ,若非空集合
,若非空集合 同时满足以下4个条件,则称
同时满足以下4个条件,则称 是“
是“ 无和划分”:
无和划分”:
①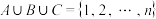 ;
;
②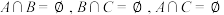 ;
;
③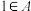 ,且
,且 中的最小元素大于
中的最小元素大于 中的最小元素;
中的最小元素;
④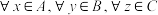 ,必有
,必有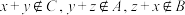 .
.
(1)若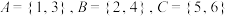 ,判断
,判断 是否是“
是否是“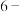 无和划分”,并说明理由.
无和划分”,并说明理由.
(2)已知 是“
是“ 无和划分”(
无和划分”( ).
).
①证明:对于任意 ,都有
,都有 ;
;
②若存在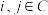 ,使得
,使得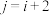 ,记
,记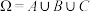 ,证明:
,证明: 中的所有奇数都属于
中的所有奇数都属于 .
.
 ,若非空集合
,若非空集合 同时满足以下4个条件,则称
同时满足以下4个条件,则称 是“
是“ 无和划分”:
无和划分”:①
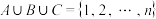 ;
;②
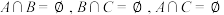 ;
;③
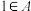 ,且
,且 中的最小元素大于
中的最小元素大于 中的最小元素;
中的最小元素;④
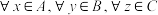 ,必有
,必有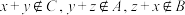 .
.(1)若
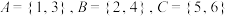 ,判断
,判断 是否是“
是否是“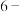 无和划分”,并说明理由.
无和划分”,并说明理由.(2)已知
 是“
是“ 无和划分”(
无和划分”( ).
).①证明:对于任意
 ,都有
,都有 ;
;②若存在
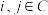 ,使得
,使得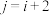 ,记
,记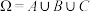 ,证明:
,证明: 中的所有奇数都属于
中的所有奇数都属于 .
.
您最近一年使用:0次
2024-06-10更新
|
118次组卷
|
2卷引用:北京市丰台区2023-2024学年高一上学期期末练习数学试卷
名校
解题方法
10 . 给定正整数 ,设集合
,设集合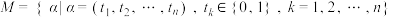 .对于集合
.对于集合 中的任意元素
中的任意元素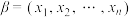 和
和 ,记
,记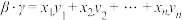 .设
.设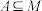 ,且集合
,且集合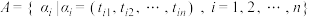 ,对于
,对于 中任意元素
中任意元素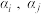 ,若
,若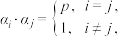 则称
则称 具有性质
具有性质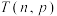 .
.
(1)判断集合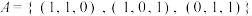 是否具有性质
是否具有性质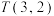 ?说明理由;
?说明理由;
(2)判断是否存在具有性质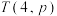 的集合
的集合 ,并加以证明.
,并加以证明.
 ,设集合
,设集合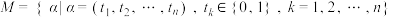 .对于集合
.对于集合 中的任意元素
中的任意元素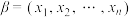 和
和 ,记
,记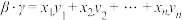 .设
.设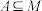 ,且集合
,且集合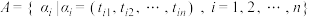 ,对于
,对于 中任意元素
中任意元素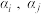 ,若
,若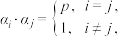 则称
则称 具有性质
具有性质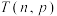 .
.(1)判断集合
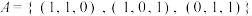 是否具有性质
是否具有性质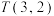 ?说明理由;
?说明理由;(2)判断是否存在具有性质
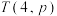 的集合
的集合 ,并加以证明.
,并加以证明.
您最近一年使用:0次
2024-01-25更新
|
305次组卷
|
4卷引用:北京市延庆区2023-2024学年高二上学期期末考试数学试卷
北京市延庆区2023-2024学年高二上学期期末考试数学试卷北京市海淀区北京交通大学附属中学2023-2024学年高二上学期期中练习数学试题(已下线)专题04 分类讨论型【讲】【北京版】2(已下线)专题1 集合新定义题(九省联考第19题模式)练



