北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京
高一
期末
2024-03-11
3579次
整体难度:
容易
考查范围:
集合与常用逻辑用语、函数与导数、平面向量、计数原理与概率统计
北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京
高一
期末
2024-03-11
3579次
整体难度:
容易
考查范围:
集合与常用逻辑用语、函数与导数、平面向量、计数原理与概率统计
一、单选题 添加题型下试题
单选题
|
较易(0.85)
名校
解题方法
2. 当 时,在同一坐标系中,函数
时,在同一坐标系中,函数 与
与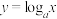 的图象是( ).
的图象是( ).
 时,在同一坐标系中,函数
时,在同一坐标系中,函数 与
与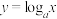 的图象是( ).
的图象是( ).A.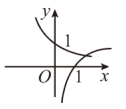 | B.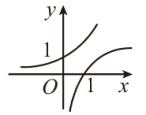 | C.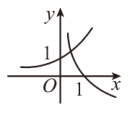 | D.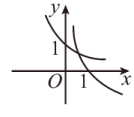 |
【知识点】 判断指数型函数的图象形状 判断对数型函数的图象形状
您最近一年使用:0次
2020-12-20更新
|
670次组卷
|
6卷引用:广东省江门市第二中学2020-2021学年高一上学期第二次考试(期中)数学试题
广东省江门市第二中学2020-2021学年高一上学期第二次考试(期中)数学试题北京市石景山区2020-2021学年高一上学期期末数学试题(已下线)专题4.8 对数函数-重难点题型检测-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)北京延庆区2022-2023学年高一上学期期末考试数学试题广东省湛江市第七中学2024届高三上学期9月月考数学试题北京市延庆区2023-2024学年高一上学期期末考试数学试卷
二、多选题 添加题型下试题
多选题
|
较易(0.85)
名校
解题方法
3. 下列函数中是奇函数且在 上单调递增的是( )
上单调递增的是( )
A.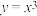 | B. |
C. | D. |
您最近一年使用:0次
2024-03-31更新
|
466次组卷
|
2卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
三、单选题 添加题型下试题
单选题
|
容易(0.94)
您最近一年使用:0次
单选题
|
容易(0.94)
7. 甲,乙两人在5天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则下列结论正确的是( )
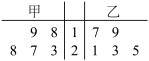
| A.在这5天中,甲加工零件数的极差小于乙加工零件数的极差 |
| B.在这5天中,甲、乙两人加工零件数的中位数相同 |
| C.在这5天中,甲日均加工零件数大于乙日均加工零件数 |
| D.在这5天中,甲加工零件数的方差小于乙加工零件数的方差 |
您最近一年使用:0次
2024-03-07更新
|
359次组卷
|
2卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
单选题
|
较易(0.85)
名校
8. 一个袋子中有大小和质地相同的4个球 其中有2个红色球(标号为1和2),2个绿色球(标号为3和4),从袋中不放回地依次随机揽出2个球,每次摸出一个球,设事件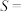 "第一次摸到红球",
"第一次摸到红球",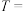 "第二次摸到红球",
"第二次摸到红球", "两次都摸到红球",
"两次都摸到红球", "两次都摸到绿球”,
"两次都摸到绿球”,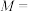 “两球颜色相同”,
“两球颜色相同”,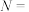 “两球颜色不同”.则下列说法错误的是( )
“两球颜色不同”.则下列说法错误的是( )
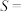 "第一次摸到红球",
"第一次摸到红球",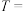 "第二次摸到红球",
"第二次摸到红球", "两次都摸到红球",
"两次都摸到红球", "两次都摸到绿球”,
"两次都摸到绿球”,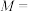 “两球颜色相同”,
“两球颜色相同”,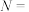 “两球颜色不同”.则下列说法错误的是( )
“两球颜色不同”.则下列说法错误的是( )A. | B. R与G互斥但不对立 |
C. | D.S与T相互独立 |
您最近一年使用:0次
2024-03-07更新
|
848次组卷
|
6卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京市延庆区2023-2024学年高一上学期期末考试数学试卷(已下线)15.3 互斥事件和独立事件(1)-【帮课堂】(苏教版2019必修第二册)(已下线)专题10.7 概率全章综合测试卷(基础篇)-举一反三系列(人教A版2019必修第二册)(已下线)专题01 高一下期末真题精选(2)-期末考点大串讲(人教A版2019必修第二册)(已下线)必考考点10 概率 专题讲解 (期末考试必考的10大核心考点)江苏省江阴市成化高级中学2023-2024学年高一下学期第二次阶段考试数学试题
单选题
|
适中(0.65)
名校
解题方法
您最近一年使用:0次
2024-03-07更新
|
2438次组卷
|
12卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京市延庆区2023-2024学年高一上学期期末考试数学试卷(已下线)8.1.2向量数量积的运算律-同步精品课堂(人教B版2019必修第三册)(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(1)-同步精品课堂(人教B版2019必修第三册)福建省华安县第一中学2023-2024学年高一下学期第一次月考数学试卷天津外国语大学附属河北外国语中学2023-2024学年高一下学期第一次月考数学试题山东省菏泽市东明县第一中学2023-2024学年高一下学期4月月考数学试题四川省绵阳市东辰学校2024届高三下学期第二学月考试数学(理科)试题辽宁省沈阳市第二十中学2023-2024学年高一下学期4月阶段测试数学试卷(已下线)专题01 平面向量-《期末真题分类汇编》(人教A版2019必修第二册)(已下线)专题01 高一下期末真题精选(1)-期末考点大串讲(人教A版2019必修第二册)(已下线)专题03 平面向量的9种常考题型归类(1)-《期末真题分类汇编》(北师大版(2019))(已下线)核心考点2 平面向量的数量积 B提升卷 (高一期末考试必考的10大核心考点)
单选题
|
较易(0.85)
10. 假设有机体生存吋碳14的含量为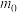 ,那么有机体死亡x年后体内碳14的含量满足的关系为
,那么有机体死亡x年后体内碳14的含量满足的关系为 (其中m₀,a都是非零实数).若测得死亡5730年后的古生物样品,体内碳14的含量为0.5,又测得死亡11460年后这类古生物样品.体内碳14的含量为0.25.如果测得某古生物样品碳14的含量为0.3,推测此古生物的死亡时间为(取
(其中m₀,a都是非零实数).若测得死亡5730年后的古生物样品,体内碳14的含量为0.5,又测得死亡11460年后这类古生物样品.体内碳14的含量为0.25.如果测得某古生物样品碳14的含量为0.3,推测此古生物的死亡时间为(取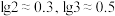 )( )
)( )
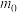 ,那么有机体死亡x年后体内碳14的含量满足的关系为
,那么有机体死亡x年后体内碳14的含量满足的关系为 (其中m₀,a都是非零实数).若测得死亡5730年后的古生物样品,体内碳14的含量为0.5,又测得死亡11460年后这类古生物样品.体内碳14的含量为0.25.如果测得某古生物样品碳14的含量为0.3,推测此古生物的死亡时间为(取
(其中m₀,a都是非零实数).若测得死亡5730年后的古生物样品,体内碳14的含量为0.5,又测得死亡11460年后这类古生物样品.体内碳14的含量为0.25.如果测得某古生物样品碳14的含量为0.3,推测此古生物的死亡时间为(取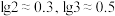 )( )
)( )| A.10550年 | B.7550年 |
| C.8550年 | D.9550年 |
【知识点】 指数式与对数式的互化 运用换底公式化简计算 指数函数模型的应用(2)
您最近一年使用:0次
四、填空题 添加题型下试题
填空题-单空题
|
容易(0.94)
您最近一年使用:0次
填空题-单空题
|
较易(0.85)
解题方法
您最近一年使用:0次
2024-03-07更新
|
835次组卷
|
9卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京市延庆区2023-2024学年高一上学期期末考试数学试卷(已下线)6.3.5平面向量数量积的坐标表示(已下线)模块一 专题2 平面向量基本定理与坐标运算(讲)(已下线)8.1.3 向量数量积的坐标运算-【帮课堂】(人教B版2019必修第三册)四川省达州外国语学校2023-2024学年高一下学期3月月考数学试题(已下线)模块一专题2 《平面向量基本定理与坐标运算》 【讲】(苏教版)(已下线)6.3.5 平面向量数量积的坐标表示——课后作业(提升版)(已下线)模块一 专题4 平面向量基本定理与坐标运算(讲)北师大版高一期中(已下线)专题03 平面向量的9种常考题型归类(1)-《期末真题分类汇编》(北师大版(2019))
填空题-双空题
|
较易(0.85)
14. 甲同学进行投篮练习,每次投中的概率都是 ,连续投3次.每次投篮互不影响.则该同学恰好只有第3次投中的概率为
,连续投3次.每次投篮互不影响.则该同学恰好只有第3次投中的概率为________ :该同学至少两次投中的概率为_________ .
 ,连续投3次.每次投篮互不影响.则该同学恰好只有第3次投中的概率为
,连续投3次.每次投篮互不影响.则该同学恰好只有第3次投中的概率为
您最近一年使用:0次
填空题-单空题
|
适中(0.65)
15. 设 ,函数
,函数  给出下列四个结论:
给出下列四个结论:
① 在区间
在区间 上单调递减;
上单调递减;
②当 存在最大值时,
存在最大值时,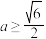 ;
;
③存在 ,
,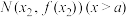 ,使得
,使得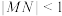 ;
;
④若存在两个不同的x,使得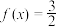 ,则a的取值范围是
,则a的取值范围是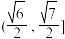 .
.
其中所有正确结论的序号是__________
 ,函数
,函数  给出下列四个结论:
给出下列四个结论:①
 在区间
在区间 上单调递减;
上单调递减;②当
 存在最大值时,
存在最大值时,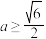 ;
;③存在
 ,
,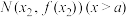 ,使得
,使得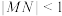 ;
;④若存在两个不同的x,使得
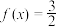 ,则a的取值范围是
,则a的取值范围是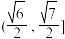 .
.其中所有正确结论的序号是
您最近一年使用:0次
五、解答题 添加题型下试题
解答题-问答题
|
较易(0.85)
名校
解题方法
16. 如图,在 中,
中,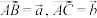 ,D为
,D为 中点,E为
中点,E为 上一点,且
上一点,且 ,
, 的延长线与
的延长线与 的交点为F.
的交点为F. 与
与 表示
表示 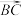 和
和 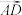
(2)用向量 与
与 表示
表示 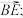
(3)求出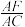 的值
的值
 中,
中,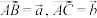 ,D为
,D为 中点,E为
中点,E为 上一点,且
上一点,且 ,
, 的延长线与
的延长线与 的交点为F.
的交点为F.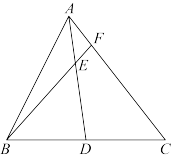
 与
与 表示
表示 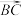 和
和 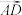
(2)用向量
 与
与 表示
表示 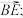
(3)求出
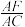 的值
的值
【知识点】 已知向量共线(平行)求参数解读 用基底表示向量解读
您最近一年使用:0次
2024-03-07更新
|
2387次组卷
|
10卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京市延庆区2023-2024学年高一上学期期末考试数学试卷(已下线)2.3 从速度的倍数到向量的数乘-同步精品课堂(北师大版2019必修第二册)(已下线)2.3 从速度的倍数到向量的数乘6种常见考法归类-【帮课堂】(北师大版2019必修第二册)甘肃省酒泉市敦煌中学2023-2024学年高一下学期3月月考数学试卷广东省江门市某校2023-2024学年高一下学期第一次质量检测数学试题新疆乌鲁木齐市第101中学2023-2024学年高一下学期第一次月考数学试卷广东省佛山市南海区南海中学分校2023-2024学年高一下学期第一次教学质量检测(4月)数学试题新疆维吾尔自治区伊犁哈萨克自治州霍尔果斯市苏港中学2023-2024学年高一下学期4月月考数学试题海南省东方市东方中学2023-2024学年高一下学期第一次月考数学试题江西省宜春市上高二中2023-2024学年高一下学期第六次(3月)月考数学试题
解答题-应用题
|
适中(0.65)
名校
解题方法
17. 为了了解某校高一学生一次体育健康测试的得分情况,一位老师采用分层抽样的方法选取了20名学生的成绩作为样本,来估计本校高一学生的得分情况,并以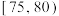 ,
,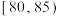 ,
,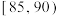 ,
,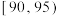 ,
,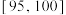 分组,作出了如图所示的频率分布直方图,规定成绩不低于90分为“优秀”.
分组,作出了如图所示的频率分布直方图,规定成绩不低于90分为“优秀”.
(2)从样本成绩优秀的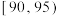 ,
,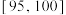 两组学生中任意选取2人,记为
两组学生中任意选取2人,记为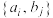 ,
, 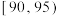 中的学生为
中的学生为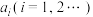 ,
, 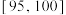 中的学生为
中的学生为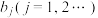 ,求这2人来自同一组的概率;
,求这2人来自同一组的概率;
(3)从成绩在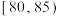 的学生中任取3名学生记为A组,从成绩在
的学生中任取3名学生记为A组,从成绩在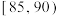 的学生它任取3名学生记为B组,这两组学生的得分记录如下:
的学生它任取3名学生记为B组,这两组学生的得分记录如下:
A组: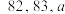 ; B组:
; B组: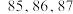 .
.
写出a为何值时,A、B两组学生得分的方差相等(结论不要求证明).
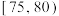 ,
,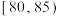 ,
,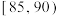 ,
,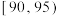 ,
,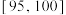 分组,作出了如图所示的频率分布直方图,规定成绩不低于90分为“优秀”.
分组,作出了如图所示的频率分布直方图,规定成绩不低于90分为“优秀”.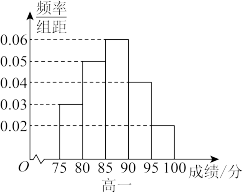
(2)从样本成绩优秀的
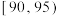 ,
,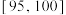 两组学生中任意选取2人,记为
两组学生中任意选取2人,记为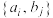 ,
, 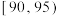 中的学生为
中的学生为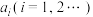 ,
, 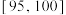 中的学生为
中的学生为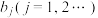 ,求这2人来自同一组的概率;
,求这2人来自同一组的概率;(3)从成绩在
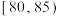 的学生中任取3名学生记为A组,从成绩在
的学生中任取3名学生记为A组,从成绩在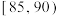 的学生它任取3名学生记为B组,这两组学生的得分记录如下:
的学生它任取3名学生记为B组,这两组学生的得分记录如下:A组:
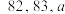 ; B组:
; B组: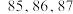 .
.写出a为何值时,A、B两组学生得分的方差相等(结论不要求证明).
您最近一年使用:0次
2024-03-07更新
|
577次组卷
|
5卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京市延庆区2023-2024学年高一上学期期末考试数学试卷(已下线)15.2 随机事件的概率-【帮课堂】(苏教版2019必修第二册)江西省宜春市丰城中学2023-2024学年高一下学期4月期中考试数学试题(已下线)重难点专题16 玩转古典概型-【帮课堂】(苏教版2019必修第二册)(已下线)专题06 概率-期末真题分类汇编(人教A版2019必修第二册)
解答题-问答题
|
适中(0.65)
解题方法
18. 已知函数①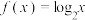 ②
②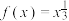 . 从这两个函数中选择一个、并完成以下问题.
. 从这两个函数中选择一个、并完成以下问题.
(1)求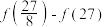 的解:
的解:
(2)在x轴上取两点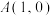 和
和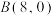 ,设线段
,设线段 的中点为C,过点A,B,C分别作x轴的垂线,与函数
的中点为C,过点A,B,C分别作x轴的垂线,与函数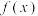 的图象交于
的图象交于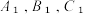 ,线段
,线段 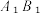 中点为M.
中点为M.
(i)求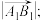
(ii)判断 与
与 的大小.并说明理由.
的大小.并说明理由.
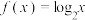 ②
②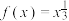 . 从这两个函数中选择一个、并完成以下问题.
. 从这两个函数中选择一个、并完成以下问题.(1)求
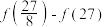 的解:
的解:(2)在x轴上取两点
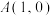 和
和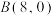 ,设线段
,设线段 的中点为C,过点A,B,C分别作x轴的垂线,与函数
的中点为C,过点A,B,C分别作x轴的垂线,与函数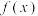 的图象交于
的图象交于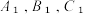 ,线段
,线段 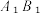 中点为M.
中点为M.(i)求
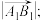
(ii)判断
 与
与 的大小.并说明理由.
的大小.并说明理由.
您最近一年使用:0次
2024-03-07更新
|
359次组卷
|
4卷引用:北京市延庆区2023-2024学年高一上学期期末考试数学试卷
北京市延庆区2023-2024学年高一上学期期末考试数学试卷(已下线)8.1.3向量数量积的坐标运算-同步精品课堂(人教B版2019必修第三册)四川省广安市友实学校2023-2024学年高一下学期3月月考数学试题(已下线)第二章平面向量及其应用章末综合检测卷(新题型)-【帮课堂】(北师大版2019必修第二册)
解答题-问答题
|
适中(0.65)
解题方法
19. 函数 的图像如图所示,定义域为
的图像如图所示,定义域为 ,其中
,其中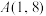 ,
,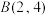 ,当
,当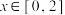 时.图像是二次函数的一部分,其中顶点
时.图像是二次函数的一部分,其中顶点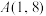 ,当
,当 时,图像是指数函数的一部分.
时,图像是指数函数的一部分.
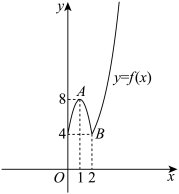
(1)求函数 的解析式:
的解析式:
(2)求不等式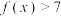 的解集:
的解集:
(3)若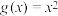 对于
对于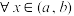 ,恒有
,恒有 恒成立.求出
恒成立.求出 的取值范围(不要求计算过程).
的取值范围(不要求计算过程).
 的图像如图所示,定义域为
的图像如图所示,定义域为 ,其中
,其中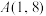 ,
,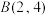 ,当
,当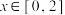 时.图像是二次函数的一部分,其中顶点
时.图像是二次函数的一部分,其中顶点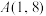 ,当
,当 时,图像是指数函数的一部分.
时,图像是指数函数的一部分.
(1)求函数
 的解析式:
的解析式:(2)求不等式
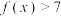 的解集:
的解集:(3)若
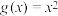 对于
对于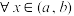 ,恒有
,恒有 恒成立.求出
恒成立.求出 的取值范围(不要求计算过程).
的取值范围(不要求计算过程).
您最近一年使用:0次
解答题-问答题
|
适中(0.65)
20. 已知函数

(1)当 时,若
时,若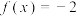 ,求x的值:
,求x的值:
(2)若 是偶函数,求出m的值:
是偶函数,求出m的值:
(3) 时,讨论方程
时,讨论方程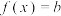 根的个数.并说明理由.
根的个数.并说明理由.


(1)当
 时,若
时,若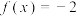 ,求x的值:
,求x的值:(2)若
 是偶函数,求出m的值:
是偶函数,求出m的值:(3)
 时,讨论方程
时,讨论方程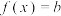 根的个数.并说明理由.
根的个数.并说明理由.
【知识点】 对数型复合函数的单调性 由奇偶性求参数 求函数零点或方程根的个数
您最近一年使用:0次
解答题-证明题
|
较难(0.4)
21. 已知集合A为非空数集.定义:
(1)若集合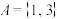 ,直接写出集合S,T;
,直接写出集合S,T;
(2)若集合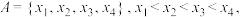 且
且 .求证:
.求证: ;
;
(3)若集合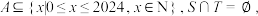 记
记 为集合A中元素的个数,求
为集合A中元素的个数,求 的最大值.
的最大值.

(1)若集合
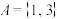 ,直接写出集合S,T;
,直接写出集合S,T;(2)若集合
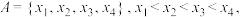 且
且 .求证:
.求证: ;
;(3)若集合
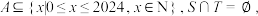 记
记 为集合A中元素的个数,求
为集合A中元素的个数,求 的最大值.
的最大值.
【知识点】 集合新定义
您最近一年使用:0次
试卷分析
导出
整体难度:适中
考查范围:集合与常用逻辑用语、函数与导数、平面向量、计数原理与概率统计
试卷题型(共 21题)
题型
数量
单选题
9
多选题
1
填空题
5
解答题
6
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 并集的概念及运算 区间的关系与运算 | |
| 2 | 0.85 | 判断指数型函数的图象形状 判断对数型函数的图象形状 | |
| 4 | 0.94 | 利用向量垂直求参数 | |
| 5 | 0.85 | 比较指数幂的大小 对数函数单调性的应用 比较对数式的大小 | |
| 6 | 0.94 | 指数幂的运算 对数的运算 | |
| 7 | 0.94 | 由茎叶图计算中位数 由茎叶图计算平均数 计算几个数据的极差、方差、标准差 | |
| 8 | 0.85 | 事件的运算及其含义 判断所给事件是否是互斥关系 互斥事件与对立事件关系的辨析 独立事件的判断 | |
| 9 | 0.65 | 已知数量积求模 | |
| 10 | 0.85 | 指数式与对数式的互化 运用换底公式化简计算 指数函数模型的应用(2) | |
| 二、多选题 | |||
| 3 | 0.85 | 函数奇偶性的定义与判断 对数函数图象的应用 判断一般幂函数的单调性 根据解析式直接判断函数的单调性 | |
| 三、填空题 | |||
| 11 | 0.85 | 具体函数的定义域 求对数型复合函数的定义域 | 单空题 |
| 12 | 0.94 | 指数幂的运算 对数的运算 | 单空题 |
| 13 | 0.85 | 向量模的坐标表示 | 单空题 |
| 14 | 0.85 | 独立事件的乘法公式 | 双空题 |
| 15 | 0.65 | 根据零点求函数解析式中的参数 分段函数的值域或最值 解分段函数不等式 分段函数的单调性 | 单空题 |
| 四、解答题 | |||
| 16 | 0.85 | 已知向量共线(平行)求参数 用基底表示向量 | 问答题 |
| 17 | 0.65 | 由频率分布直方图计算频率、频数、样本容量、总体容量 计算几个数据的极差、方差、标准差 计算古典概型问题的概率 | 应用题 |
| 18 | 0.65 | 指数幂的运算 对数的运算 用坐标表示平面向量 向量模的坐标表示 | 问答题 |
| 19 | 0.65 | 求二次函数的解析式 求指数函数解析式 对数的运算性质的应用 由指数函数的单调性解不等式 | 问答题 |
| 20 | 0.65 | 对数型复合函数的单调性 由奇偶性求参数 求函数零点或方程根的个数 | 问答题 |
| 21 | 0.4 | 集合新定义 | 证明题 |

 ,集合
,集合 ,则
,则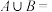 (
(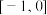
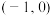
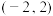

 ,
, ,若
,若 ⊥
⊥ ,则(
,则(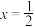



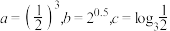 的大小关系为(
的大小关系为(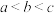
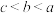


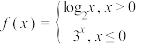 ,则
,则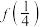 的值为(
的值为(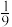


 ,E为线段
,E为线段 上的动点,求
上的动点,求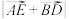 的取值范围(
的取值范围(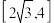
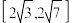
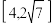
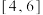
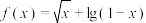 的定义域为
的定义域为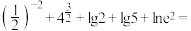
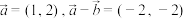 ,则
,则 =
=

