1 . 已知函数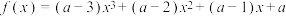 若对任意
若对任意 ,曲线
,曲线 在点
在点 和
和 处的切线互相平行或重合,则实数
处的切线互相平行或重合,则实数 ( )
( )
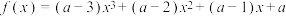 若对任意
若对任意 ,曲线
,曲线 在点
在点 和
和 处的切线互相平行或重合,则实数
处的切线互相平行或重合,则实数 ( )
( )| A.0 | B.1 | C.2 | D.3 |
您最近半年使用:0次
解题方法
2 . 已知函数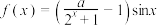 是偶函数,则实数
是偶函数,则实数
______ .
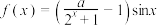 是偶函数,则实数
是偶函数,则实数
您最近半年使用:0次
2024·全国·模拟预测
3 . 已知函数 ,且
,且 ,则关于
,则关于 的不等式
的不等式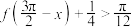 的解集为( )
的解集为( )
 ,且
,且 ,则关于
,则关于 的不等式
的不等式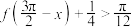 的解集为( )
的解集为( )A.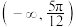 | B. | C. | D.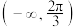 |
您最近半年使用:0次
解题方法
4 . 已知 ,函数
,函数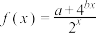 是奇函数,则
是奇函数,则
___________ ,
___________ .
 ,函数
,函数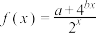 是奇函数,则
是奇函数,则

您最近半年使用:0次
解题方法
5 . 设 ,函数
,函数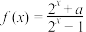 .
.
(1)求 的值,使得
的值,使得 为奇函数;
为奇函数;
(2)若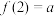 ,求满足
,求满足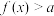 的实数
的实数 的取值范围.
的取值范围.
 ,函数
,函数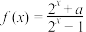 .
.(1)求
 的值,使得
的值,使得 为奇函数;
为奇函数;(2)若
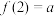 ,求满足
,求满足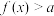 的实数
的实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
6 . 已知 为均不等于1且不相等的正实数.若函数
为均不等于1且不相等的正实数.若函数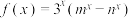 是奇函数,则
是奇函数,则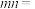
___________ .
 为均不等于1且不相等的正实数.若函数
为均不等于1且不相等的正实数.若函数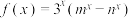 是奇函数,则
是奇函数,则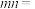
您最近半年使用:0次
7 . 设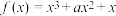 (
( ),若
),若 为奇函数,则曲线
为奇函数,则曲线 在点
在点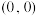 处的切线方程为
处的切线方程为___________ .
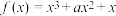 (
( ),若
),若 为奇函数,则曲线
为奇函数,则曲线 在点
在点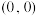 处的切线方程为
处的切线方程为
您最近半年使用:0次
解题方法
8 . 下列说法正确的个数为( )
① 为奇函数;
为奇函数;
②不存在 ,使得
,使得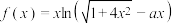 为偶函数;
为偶函数;
③存在非零实数 ,使得
,使得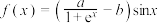 为偶函数.
为偶函数.
①
 为奇函数;
为奇函数;②不存在
 ,使得
,使得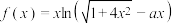 为偶函数;
为偶函数;③存在非零实数
 ,使得
,使得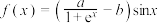 为偶函数.
为偶函数.| A.0 | B.1 | C.2 | D.3 |
您最近半年使用:0次
名校
解题方法
9 . 若函数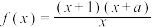 为奇函数,则实数
为奇函数,则实数 ( )
( )
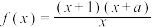 为奇函数,则实数
为奇函数,则实数 ( )
( )| A.1 | B. | C.2 | D. |
您最近半年使用:0次

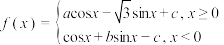 ,则
,则 的值为
的值为

