1 . 正项等比数列 的前
的前 项和为
项和为 ,若
,若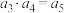 ,
,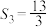 ,则
,则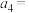 ( )
( )
 的前
的前 项和为
项和为 ,若
,若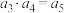 ,
,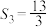 ,则
,则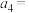 ( )
( )| A.9 | B.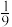 | C.9或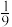 | D.18 |
您最近一年使用:0次
解题方法
2 . 设数列 满足
满足 ,则
,则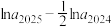 的值为
的值为__________ .
 满足
满足 ,则
,则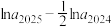 的值为
的值为
您最近一年使用:0次
名校
解题方法
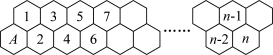
3 . 一只蜜蜂从蜂房 出发向右爬,每次只能爬向右侧相邻的两个蜂房(如图),例如:从蜂房
出发向右爬,每次只能爬向右侧相邻的两个蜂房(如图),例如:从蜂房 只能爬到1号或2号蜂房,从1号蜂房只能爬到2号或3号蜂房……以此类推,用
只能爬到1号或2号蜂房,从1号蜂房只能爬到2号或3号蜂房……以此类推,用 表示蜜蜂爬到
表示蜜蜂爬到 号蜂房的方法数,则
号蜂房的方法数,则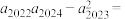 ( )
( )
 出发向右爬,每次只能爬向右侧相邻的两个蜂房(如图),例如:从蜂房
出发向右爬,每次只能爬向右侧相邻的两个蜂房(如图),例如:从蜂房 只能爬到1号或2号蜂房,从1号蜂房只能爬到2号或3号蜂房……以此类推,用
只能爬到1号或2号蜂房,从1号蜂房只能爬到2号或3号蜂房……以此类推,用 表示蜜蜂爬到
表示蜜蜂爬到 号蜂房的方法数,则
号蜂房的方法数,则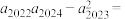 ( )
( )
| A.1 | B. | C.2 | D. |
您最近一年使用:0次
名校
4 . 设等比数列 的前n项和是
的前n项和是 .已知
.已知 ,则
,则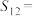
__________ .
 的前n项和是
的前n项和是 .已知
.已知 ,则
,则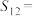
您最近一年使用:0次
名校
5 . 设 是等比数列,且
是等比数列,且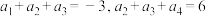 ,则
,则
__________ .
 是等比数列,且
是等比数列,且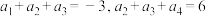 ,则
,则
您最近一年使用:0次
2024-07-20更新
|
211次组卷
|
2卷引用:江西省九江市2023-2024学年高二下学期7月期末考试数学试题
6 . 已知各项均为正数的等比数列 ,
,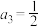 ,
,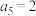 ,则
,则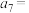
______ ; 前
前 项积
项积 的最小值为
的最小值为______ .
 ,
,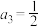 ,
,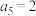 ,则
,则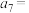
 前
前 项积
项积 的最小值为
的最小值为
您最近一年使用:0次
7 . 设数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则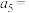 ( )
( )
 的前
的前 项和为
项和为 ,若
,若 ,则
,则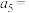 ( )
( )| A.16 | B.31 | C.47 | D.63 |
您最近一年使用:0次
8 . 如图,正方形 的边长为
的边长为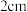 ,取正方形
,取正方形 各边的中点
各边的中点 ,
, ,
, ,
, ,作第2个正方形
,作第2个正方形 ,然后再取正方形
,然后再取正方形 各边的中点
各边的中点 ,
, ,
, ,
, ,作第3个正方形的
,作第3个正方形的 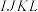 ,依此方法一直继续下去. 设第
,依此方法一直继续下去. 设第 个正方形面积为
个正方形面积为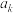 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的边长为
的边长为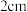 ,取正方形
,取正方形 各边的中点
各边的中点 ,
, ,
, ,
, ,作第2个正方形
,作第2个正方形 ,然后再取正方形
,然后再取正方形 各边的中点
各边的中点 ,
, ,
, ,
, ,作第3个正方形的
,作第3个正方形的 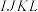 ,依此方法一直继续下去. 设第
,依此方法一直继续下去. 设第 个正方形面积为
个正方形面积为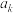 ,则下列结论正确的是( )
,则下列结论正确的是( )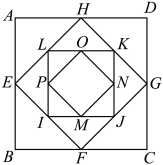
A.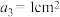 |
B.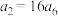 |
C.前6个正方形面积和为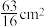 |
D.如果这个作图过程可以一直继续下去,那么这些正方形的面积之和将趋近 |
您最近一年使用:0次
解题方法
9 . 设等比数列 的前n项和为
的前n项和为 ,若
,若 ,
,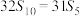 ,则
,则 ( )
( )
 的前n项和为
的前n项和为 ,若
,若 ,
,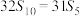 ,则
,则 ( )
( )A.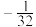 | B.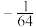 | C. | D. |
您最近一年使用:0次
10 . 数列 为等比数列,若
为等比数列,若 ,
,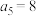 ,则
,则 .正确吗?为什么?
.正确吗?为什么?
 为等比数列,若
为等比数列,若 ,
,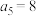 ,则
,则 .正确吗?为什么?
.正确吗?为什么?
您最近一年使用:0次



