2024高三·全国·专题练习
1 . 掷一枚质地均匀的骰子,得分规则如下:若出现的点数为1,则得1分;若出现的点数为2或3,则得2分;若出现的点数为4或5或6,则得3分.
(1)记 为连续掷这枚骰子2次的总得分,求
为连续掷这枚骰子2次的总得分,求 的数学期望;
的数学期望;
(2)现在将得分规则变更如下:若出现的点数为1或2,则得2分,其他情况都得1分.反复掷这枚骰子,设总得分为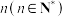 的概率为
的概率为 ,证明:数列
,证明:数列 为等比数列.
为等比数列.
(1)记
 为连续掷这枚骰子2次的总得分,求
为连续掷这枚骰子2次的总得分,求 的数学期望;
的数学期望;(2)现在将得分规则变更如下:若出现的点数为1或2,则得2分,其他情况都得1分.反复掷这枚骰子,设总得分为
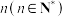 的概率为
的概率为 ,证明:数列
,证明:数列 为等比数列.
为等比数列.
您最近半年使用:0次
解题方法
2 . 数列 满足:
满足: ,则下列结论中正确的是( )
,则下列结论中正确的是( )
 满足:
满足: ,则下列结论中正确的是( )
,则下列结论中正确的是( )A. | B. 是等比数列 是等比数列 |
C. | D. |
您最近半年使用:0次
3 . 正项数列 满足
满足 ,
,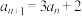 .
.
(1)证明:数列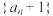 为等比数列;
为等比数列;
(2)求数列 的前
的前 项和
项和 .
.
 满足
满足 ,
,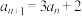 .
.(1)证明:数列
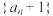 为等比数列;
为等比数列;(2)求数列
 的前
的前 项和
项和 .
.
您最近半年使用:0次
4 . 已知数列 满足
满足 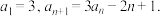
(1)求证: 为等比数列;
为等比数列;
(2)数列 的前n项和为
的前n项和为 ,求数列
,求数列 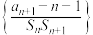 的前n项和
的前n项和 .
.
 满足
满足 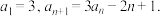
(1)求证:
 为等比数列;
为等比数列;(2)数列
 的前n项和为
的前n项和为 ,求数列
,求数列 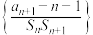 的前n项和
的前n项和 .
.
您最近半年使用:0次
2024·全国·模拟预测
5 . 记 为数列
为数列 的前
的前 项的积,
项的积,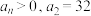 ,
,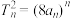 .
.
(1)求 ,并证明
,并证明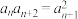 .
.
(2)从下面两个条件中选一个,求数列 的前
的前 项和
项和 .
.
① ;②
;②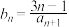 .
.
 为数列
为数列 的前
的前 项的积,
项的积,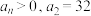 ,
,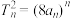 .
.(1)求
 ,并证明
,并证明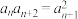 .
.(2)从下面两个条件中选一个,求数列
 的前
的前 项和
项和 .
.①
 ;②
;②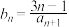 .
.
您最近半年使用:0次
6 . 在数列 中,
中,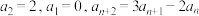 .
.
(1)证明: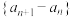 是等比数列.
是等比数列.
(2)求 的通项公式.
的通项公式.
(3)求数列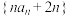 的前
的前 项和
项和 .
.
 中,
中,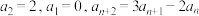 .
.(1)证明:
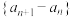 是等比数列.
是等比数列.(2)求
 的通项公式.
的通项公式.(3)求数列
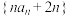 的前
的前 项和
项和 .
.
您最近半年使用:0次
7 . 甲进行摸球跳格游戏.图上标有第1格,第2格, ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.
(1)甲在一次摸球中摸出红球的个数记为 ,求
,求 的分布列和期望;
的分布列和期望;
(2)证明:数列 为等比数列,并求
为等比数列,并求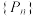 的通项公式.
的通项公式.
 ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.(1)甲在一次摸球中摸出红球的个数记为
 ,求
,求 的分布列和期望;
的分布列和期望;(2)证明:数列
 为等比数列,并求
为等比数列,并求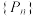 的通项公式.
的通项公式.
您最近半年使用:0次
8 . 已知数列 的前
的前 项和为
项和为 ,且
,且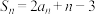 .
.
(1)证明数列 为等比数列,并求
为等比数列,并求 的通项公式;
的通项公式;
(2)在 和
和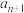 之间插入
之间插入 个数,使这
个数,使这 个数组成一个公差为
个数组成一个公差为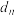 的等差数列,求数列
的等差数列,求数列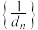 的前
的前 项和
项和 .
.
(3)若对于任意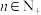 ,数列
,数列 的前
的前 项和
项和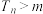 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的前
的前 项和为
项和为 ,且
,且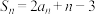 .
.(1)证明数列
 为等比数列,并求
为等比数列,并求 的通项公式;
的通项公式;(2)在
 和
和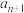 之间插入
之间插入 个数,使这
个数,使这 个数组成一个公差为
个数组成一个公差为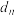 的等差数列,求数列
的等差数列,求数列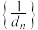 的前
的前 项和
项和 .
.(3)若对于任意
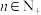 ,数列
,数列 的前
的前 项和
项和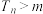 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
9 . 已知数列 的前n项和为
的前n项和为 ,
,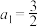 ,且
,且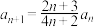 ,若不等式
,若不等式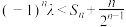 对一切
对一切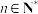 恒成立,则
恒成立,则 的取值范围为( )
的取值范围为( )
 的前n项和为
的前n项和为 ,
,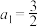 ,且
,且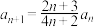 ,若不等式
,若不等式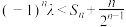 对一切
对一切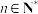 恒成立,则
恒成立,则 的取值范围为( )
的取值范围为( )A. 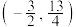 | B. 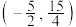 | C. 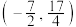 | D. 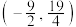 |
您最近半年使用:0次
7日内更新
|
551次组卷
|
7卷引用:河南省开封高级中学2022-2023学年高三下学期核心模拟卷(中)理科数学(三)试题
河南省开封高级中学2022-2023学年高三下学期核心模拟卷(中)理科数学(三)试题(已下线)专题11 数列前n项和的求法 微点6 错位相减法求和(已下线)专题04 数列(6)(已下线)数列与不等式(已下线)专题5-2数列递推及通项应用-2(已下线)专题8 数列与不等式恒成立问题(一题多解)河南省信阳高级中学2023-2024学年高二下学期4月月考数学试题
10 . 已知数列 的前
的前 项和为
项和为 ,
, ,且
,且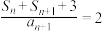 .
.
(1)证明:数列 为等比数列,并求其通项公式;
为等比数列,并求其通项公式;
(2)若__________,求数列 的前
的前 项和
项和 .
.
从① ;②
;②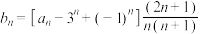 ;③
;③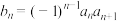 ,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
 的前
的前 项和为
项和为 ,
, ,且
,且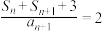 .
.(1)证明:数列
 为等比数列,并求其通项公式;
为等比数列,并求其通项公式;(2)若__________,求数列
 的前
的前 项和
项和 .
.从①
 ;②
;②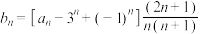 ;③
;③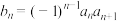 ,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
您最近半年使用:0次



