名校
解题方法
1 . 已知数列 的前
的前 项和为
项和为 ,且
,且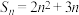 ,数列
,数列 满足
满足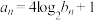 .
.
(1)求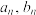 ;
;
(2)设 ,数列
,数列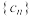 的前
的前 项和为
项和为 ,求
,求 .
.
 的前
的前 项和为
项和为 ,且
,且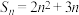 ,数列
,数列 满足
满足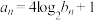 .
.(1)求
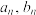 ;
;(2)设
 ,数列
,数列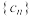 的前
的前 项和为
项和为 ,求
,求 .
.
您最近一年使用:0次
2 . 已知数列 为无穷项等比数列,
为无穷项等比数列, 为其前n项和,
为其前n项和, ,则“
,则“ 存在最小项”是“
存在最小项”是“ ”的( )
”的( )
 为无穷项等比数列,
为无穷项等比数列, 为其前n项和,
为其前n项和, ,则“
,则“ 存在最小项”是“
存在最小项”是“ ”的( )
”的( )| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
3 . 已知数列 的前
的前 项和为
项和为 ,其中
,其中 ,且
,且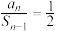 .
.
(1)求 的通项公式.
的通项公式.
(2)设 ,求
,求 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,其中
,其中 ,且
,且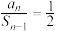 .
.(1)求
 的通项公式.
的通项公式.(2)设
 ,求
,求 的前
的前 项和
项和 .
.
您最近一年使用:0次
昨日更新
|
1492次组卷
|
5卷引用:江西省新余市第四中学2024届高三下学期高考模拟数学试题
江西省新余市第四中学2024届高三下学期高考模拟数学试题(已下线)4.4 数列求和 强化考点训练(已下线)周测12 等差数列和等比数列 (基础卷)(一轮好卷)(已下线)周测13数列通项公式、求和(一轮好卷复盘卷)内蒙古自治区赤峰市红山区赤峰二中2024-2025学年高三上学期10月月考数学试题
名校
解题方法
4 . 已知数列 的前n项和
的前n项和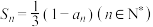 ,若
,若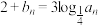 ,且数列
,且数列 满足
满足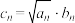 ,若集合
,若集合 中有三个元素,则实数λ的取值范围( )
中有三个元素,则实数λ的取值范围( )
 的前n项和
的前n项和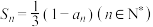 ,若
,若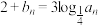 ,且数列
,且数列 满足
满足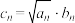 ,若集合
,若集合 中有三个元素,则实数λ的取值范围( )
中有三个元素,则实数λ的取值范围( )A. | B.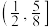 |
C. | D.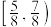 |
您最近一年使用:0次
名校
解题方法
5 . 已知数列 满足
满足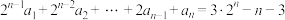 ,若
,若 ,则数列
,则数列 的前n项和
的前n项和
_________ .
 满足
满足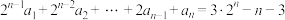 ,若
,若 ,则数列
,则数列 的前n项和
的前n项和
您最近一年使用:0次
解题方法
6 . 已知数列 的前
的前 项和
项和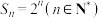 ,则
,则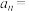
____________ .
 的前
的前 项和
项和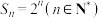 ,则
,则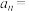
您最近一年使用:0次
7 . 已知数列 的前n项和为
的前n项和为 ,且
,且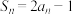 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记集合 ,若M中有3个元素,求
,若M中有3个元素,求 的取值范围;
的取值范围;
(3)是否存在等差数列 ,使得
,使得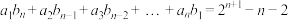 对一切
对一切 都成立?若存在,写出
都成立?若存在,写出 通项并证明上式成立;若不存在,说明理由.
通项并证明上式成立;若不存在,说明理由.
 的前n项和为
的前n项和为 ,且
,且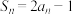 .
.(1)求数列
 的通项公式;
的通项公式;(2)记集合
 ,若M中有3个元素,求
,若M中有3个元素,求 的取值范围;
的取值范围;(3)是否存在等差数列
 ,使得
,使得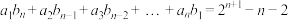 对一切
对一切 都成立?若存在,写出
都成立?若存在,写出 通项并证明上式成立;若不存在,说明理由.
通项并证明上式成立;若不存在,说明理由.
您最近一年使用:0次
名校
解题方法
8 . 设数列 满足
满足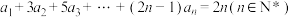 .则数列
.则数列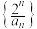 的前n项和为
的前n项和为_______ .
 满足
满足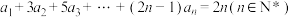 .则数列
.则数列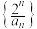 的前n项和为
的前n项和为
您最近一年使用:0次
2024高二·全国·专题练习
解题方法
9 . 已知数列 的前n项和为
的前n项和为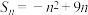 ,则该数列的通项公式为
,则该数列的通项公式为______ .
 的前n项和为
的前n项和为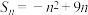 ,则该数列的通项公式为
,则该数列的通项公式为
您最近一年使用:0次
2024高二·全国·专题练习
名校
解题方法
10 . 已知数列 的前n项和
的前n项和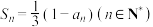 .若
.若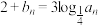 ,且数列
,且数列 满足
满足 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求证:数列 的前n项和
的前n项和 ;
;
(3)若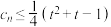 对一切
对一切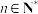 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的前n项和
的前n项和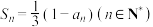 .若
.若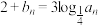 ,且数列
,且数列 满足
满足 .
.(1)求证:数列
 是等差数列;
是等差数列;(2)求证:数列
 的前n项和
的前n项和 ;
;(3)若
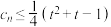 对一切
对一切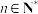 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
1090次组卷
|
4卷引用:4.3.2等比数列的前n项和公式 第三课 知识扩展延伸
(已下线)4.3.2等比数列的前n项和公式 第三课 知识扩展延伸(已下线)第四章综合 第一练 考点强化训练内蒙古自治区巴彦淖尔市第一中学2025届高三上学期第三次学业诊断(10月)数学试卷江苏省苏州市吴江平望中学2024-2025学年高二上学期10月月考数学试题



