名校
解题方法
1 . 为了研究昼夜温差与引发感冒的关系,医务人员对某高中在同一时间段相同温差下的学生感冒情况进行抽样调研,所得数据统计如表1所示,并将男生感冒的人数与温差情况统计如表2所示.
表1
表2
(1)写出m,n,p的值;
(2)依据小概率值 的独立性检验判断是否可以认为在相同的温差下“性别”与“患感冒的情况”具有相关性;
的独立性检验判断是否可以认为在相同的温差下“性别”与“患感冒的情况”具有相关性;
(3)根据表2数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(若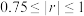 ,则认为y与x线性相关性很强;若
,则认为y与x线性相关性很强;若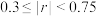 ,则认为y与x线性相关性一般;若
,则认为y与x线性相关性一般;若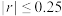 ,则认为y与x线性相关性较弱).
,则认为y与x线性相关性较弱).
附表:
参考公式及数据: ,其中
,其中 .
.
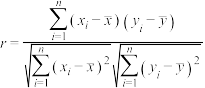 ,
,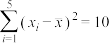 ,
,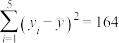 ,
,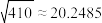 .
.
表1
性别 | 患感冒的情况 | 合计 | |
患感冒人数 | 不患感冒人数 | ||
男生 | 30 | 70 | 100 |
女生 | 42 | 58 | p |
合计 | m | n | 200 |
温差x | 6 | 7 | 8 | 9 | 10 |
患感冒人数y | 8 | 10 | 14 | 20 | 23 |
(2)依据小概率值
 的独立性检验判断是否可以认为在相同的温差下“性别”与“患感冒的情况”具有相关性;
的独立性检验判断是否可以认为在相同的温差下“性别”与“患感冒的情况”具有相关性;(3)根据表2数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(若
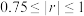 ,则认为y与x线性相关性很强;若
,则认为y与x线性相关性很强;若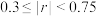 ,则认为y与x线性相关性一般;若
,则认为y与x线性相关性一般;若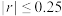 ,则认为y与x线性相关性较弱).
,则认为y与x线性相关性较弱).附表:
 | 0.100 | 0.050 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
参考公式及数据:
 ,其中
,其中 .
.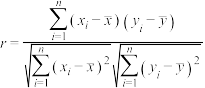 ,
,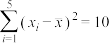 ,
,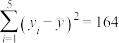 ,
,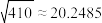 .
.
您最近一年使用:0次
2023-08-15更新
|
138次组卷
|
2卷引用:广西玉林市博白县中学2024届高三上学期开学考试数学试题
名校
解题方法
2 . 某骑行爱好者近段时间在专业人士指导下对骑行情况进行了统计,各次骑行期间的身体综合指标评分x与对应用时y(单位:小时)如下表:
(1)由上表数据看出,可用线性回归模型拟合 与
与 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立 关于
关于 的回归方程.
的回归方程.
参考数据和参考公式:相关系数 ,
,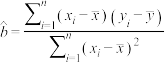 ,
, ,
,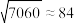
身体综合指标评分 | 1 | 2 | 3 | 4 | 5 |
用时( /小时) /小时) | 9.5 | 8.6 | 7.8 | 7 | 6.1 |
 与
与 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;(2)建立
 关于
关于 的回归方程.
的回归方程.参考数据和参考公式:相关系数
 ,
,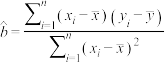 ,
, ,
,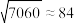
您最近一年使用:0次
2023-08-05更新
|
428次组卷
|
10卷引用:广西玉林市北流市2023届高三年级教学质量检测数学(理)试题
3 . 2016~2020年广西城乡居民人均可支配收入的柱形图如下图所示.
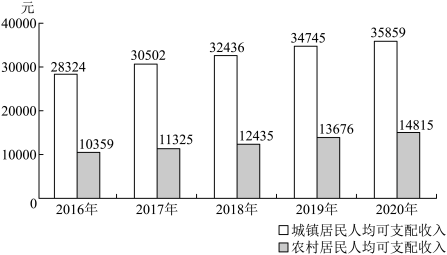
(1)不考虑价格因素,求广西2020年农村居民人均可支配收入的年增长率(结果精确到0.15%).
(2)现欲了解广西各年城镇居民人均可支配收入y(单位,元)与农村居民人均可支配收入x(单位:元)是否存在较好的线性关系.设广西2016年城镇居民人均可支配收入为y1元,农村居民人均可支配收入为 元,2017年对应的数据分别为
元,2017年对应的数据分别为 ,
, ,2018年对应的数据分别为
,2018年对应的数据分别为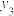 、
、 ,2019年对应的数据分别为
,2019年对应的数据分别为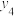 ,
, ,2020年对应的数据分别为
,2020年对应的数据分别为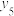 ,
,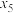 .根据图中的五组数据,得到
.根据图中的五组数据,得到 关于x的线性回归方程为
关于x的线性回归方程为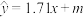 ,试问y关于x的线性相关系数r是否大于0.95,并判断y与x之间是否存在较好的线性关系.
,试问y关于x的线性相关系数r是否大于0.95,并判断y与x之间是否存在较好的线性关系.
参考数据: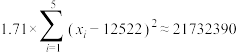 ,
,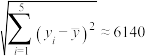 ,
, .
.
附:样本的相关系数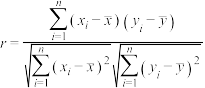 ,
,
线性回归方程 中的系数
中的系数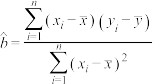 ,
, .
.

(1)不考虑价格因素,求广西2020年农村居民人均可支配收入的年增长率(结果精确到0.15%).
(2)现欲了解广西各年城镇居民人均可支配收入y(单位,元)与农村居民人均可支配收入x(单位:元)是否存在较好的线性关系.设广西2016年城镇居民人均可支配收入为y1元,农村居民人均可支配收入为
 元,2017年对应的数据分别为
元,2017年对应的数据分别为 ,
, ,2018年对应的数据分别为
,2018年对应的数据分别为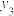 、
、 ,2019年对应的数据分别为
,2019年对应的数据分别为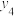 ,
, ,2020年对应的数据分别为
,2020年对应的数据分别为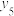 ,
,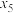 .根据图中的五组数据,得到
.根据图中的五组数据,得到 关于x的线性回归方程为
关于x的线性回归方程为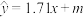 ,试问y关于x的线性相关系数r是否大于0.95,并判断y与x之间是否存在较好的线性关系.
,试问y关于x的线性相关系数r是否大于0.95,并判断y与x之间是否存在较好的线性关系.参考数据:
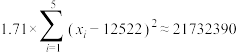 ,
,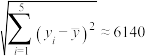 ,
, .
.附:样本的相关系数
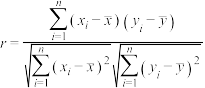 ,
,线性回归方程
 中的系数
中的系数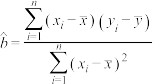 ,
, .
.
您最近一年使用:0次
2023-05-03更新
|
419次组卷
|
9卷引用:广西壮族自治区玉林市2023届高三二模数学(文)试题
广西壮族自治区玉林市2023届高三二模数学(文)试题广西壮族自治区玉林市2023届高三二模数学(理)试题广西2023届高三模拟考试数学(理)试题(已下线)专题17计数原理与概率统计(解答题)(已下线)专题17计数原理与概率统计(解答题)(已下线)模块三 专题8 成对数据的统计分析--基础夯实练)(人教A版)(已下线)模块三 专题6 统计案例--基础夯实练(北师大2019版 高二)(已下线)模块三 专题7 统计--(基础夯实练)(苏教版)(已下线)8.1成对数据的相关分析(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)
名校
解题方法
4 . 2015年7月31日,在吉隆坡举行的国际奥委会第128次全会上,北京获得2022年冬奥会举办权.在申冬奥过程中,中国正式向国际社会作出“带动三亿人参与冰雪运动”的庄严承诺.这一承诺,既是我国为国际奥林匹克运动做出重大贡献的大国担当展现,也是根据我国经济水平和全民健身需求做出的群众性运动的战略部署.从北京冬奥会申办成功到2021年10月,全国参与冰雪运动人数累计达到3.46亿,实现了“带动三亿人参与冰雪运动”的目标,这是北京冬奥会给予全球冬季体育运动和奥林匹克运动的最为重要的遗产,可以说是2022年北京冬奥会的第一块金牌.“冬奥热”带动“冰雪热”,也带动了冰雪经济,以冰雪运动为主要内容的冰雪旅游近年来发展迅速,2016至2022六个冰雪季的旅游人次y(单位亿)的数据如下表:
(1)求y与t的相关系数(精确到0.01),并回答y与t的线性相关关系的强弱;
(2)因受疫情影响,现将2019—2020年度的异常数据剔除,用剩下的5个年度数据(年度代号不变),求y关于t的线性回归方程(系数精确到0.01),并推测没有疫情情况下,2019—2020年度冰雪旅游人次的估计值.
附注:参考数据: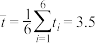 ,
,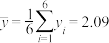 ,
,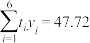 ,
,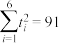 ,
,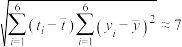 .参考公式:相关系数
.参考公式:相关系数 ,回归直线的斜率和截距的最小二乘估计公式分别为:
,回归直线的斜率和截距的最小二乘估计公式分别为: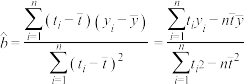 ,
,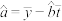
| 年度 | 2016—2017 | 2017—2018 | 2018—2019 | 2019—2020 | 2020—2021 | 2021—2022 |
| 年度代号t | 1 | 2 | 3 | 4 | 5 | 6 |
| 旅游人次y | 1.7 | 1.97 | 2.24 | 0.94 | 2.54 | 3.15 |
(2)因受疫情影响,现将2019—2020年度的异常数据剔除,用剩下的5个年度数据(年度代号不变),求y关于t的线性回归方程(系数精确到0.01),并推测没有疫情情况下,2019—2020年度冰雪旅游人次的估计值.
附注:参考数据:
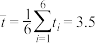 ,
,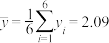 ,
,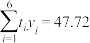 ,
,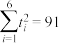 ,
,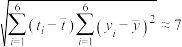 .参考公式:相关系数
.参考公式:相关系数 ,回归直线的斜率和截距的最小二乘估计公式分别为:
,回归直线的斜率和截距的最小二乘估计公式分别为: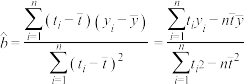 ,
,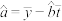
您最近一年使用:0次
2022-07-22更新
|
1581次组卷
|
7卷引用:广西壮族自治区玉林市北流市实验中学2022-2023学年高二下学期5月月考数学试题
广西壮族自治区玉林市北流市实验中学2022-2023学年高二下学期5月月考数学试题吉林省东北师范大学附属中学2022届高三第五次模拟考试文科数学试题(已下线)第09讲 高考中的概率与统计 (精讲) -1(已下线)专题6回归方程运算(提升版)(已下线)考向38统计与统计案例(重点)-2陕西省西安市陕西师范大学附属中学渭北中学2023届高三三模理科数学试题(已下线)专题21 概率与统计的综合运用(13大题型)(练习)
解题方法
5 . 新个体经济是中国经济社会数字化转型条件下出现的新生事物,指微商电商,网络直播、职业创作者等,下表是2021年1至4月份某市新增“微商电商”的统计数据:
(1)请利用所给数据求新增微商电商个数 与月份
与月份 之间的线性回归方程
之间的线性回归方程 ,并预测该市2021年5月新增“微商电商”的个数(结果用四舍五入法保留整数);
,并预测该市2021年5月新增“微商电商”的个数(结果用四舍五入法保留整数);
(2)一般认为当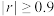 时,线性回归方程的拟合效果非常好;当
时,线性回归方程的拟合效果非常好;当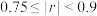 时,线性回归方程的拟合效果良好.试问该线性回归方程的拟合效果是非常好还是良好?说明你的理由.
时,线性回归方程的拟合效果良好.试问该线性回归方程的拟合效果是非常好还是良好?说明你的理由.
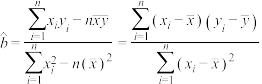 ,
, ,
, ,
,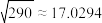 ,
,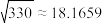 ,
, .
.
月份 | 1 | 2 | 3 | 4 |
新增微商电商个数 | 90 | 105 | 125 | 140 |
 与月份
与月份 之间的线性回归方程
之间的线性回归方程 ,并预测该市2021年5月新增“微商电商”的个数(结果用四舍五入法保留整数);
,并预测该市2021年5月新增“微商电商”的个数(结果用四舍五入法保留整数);(2)一般认为当
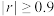 时,线性回归方程的拟合效果非常好;当
时,线性回归方程的拟合效果非常好;当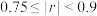 时,线性回归方程的拟合效果良好.试问该线性回归方程的拟合效果是非常好还是良好?说明你的理由.
时,线性回归方程的拟合效果良好.试问该线性回归方程的拟合效果是非常好还是良好?说明你的理由.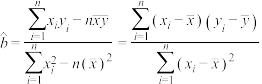 ,
, ,
, ,
,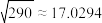 ,
,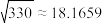 ,
, .
.
您最近一年使用:0次
2022-04-07更新
|
890次组卷
|
6卷引用:广西玉林市(玉实、玉一、北高、容高、岑中)五校联考2021-2022学年高二上学期期中质量检测数学试题
解题方法
6 . 某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差(x℃, )和患感冒的小朋友人数(y/人)的数据如下:
)和患感冒的小朋友人数(y/人)的数据如下:
其中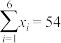 ,
,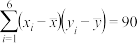 ,
,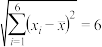 .
.
(1)请用相关系数(精确到0.01)加以说明是否可用线性回归模型拟合y与x的关系;
(2)建立y关于x的回日方程,预测当昼夜温差升高4℃时患感冒的小朋友的人数会有什么变化?
参考数据: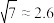 .
.
参考公式:相关系数: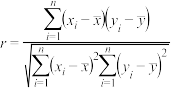 ,
,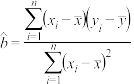 ,
,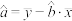
 )和患感冒的小朋友人数(y/人)的数据如下:
)和患感冒的小朋友人数(y/人)的数据如下:| 温差x |  |  |  |  | 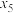 | 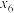 |
| 患感冒人数y | 8 | 11 | 14 | 20 | 23 | 26 |
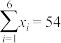 ,
,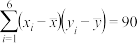 ,
,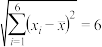 .
.(1)请用相关系数(精确到0.01)加以说明是否可用线性回归模型拟合y与x的关系;
(2)建立y关于x的回日方程,预测当昼夜温差升高4℃时患感冒的小朋友的人数会有什么变化?
参考数据:
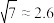 .
.参考公式:相关系数:
 ,
, ,
,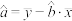
您最近一年使用:0次



