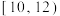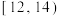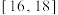名校
解题方法
1 . 在一次支教活动中,甲、乙两校各派出 名教师参与活动,其中甲校派出2名男教师和1名女教师(记两名男教师为
名教师参与活动,其中甲校派出2名男教师和1名女教师(记两名男教师为 、
、 ,女教师为
,女教师为 ),乙校派出
),乙校派出 名男教师和
名男教师和 名女教师(记男教师为
名女教师(记男教师为 ,两名女教师为
,两名女教师为 、
、 ).
).
(1)若从两校参加活动的教师中各任选 名,写出所有可能的结果,并求选出的
名,写出所有可能的结果,并求选出的 名教师性别相同的概率;
名教师性别相同的概率;
(2)若从报名的 名教师中任选
名教师中任选 名,求选出的
名,求选出的 名教师来自同一学校的概率.
名教师来自同一学校的概率.
 名教师参与活动,其中甲校派出2名男教师和1名女教师(记两名男教师为
名教师参与活动,其中甲校派出2名男教师和1名女教师(记两名男教师为 、
、 ,女教师为
,女教师为 ),乙校派出
),乙校派出 名男教师和
名男教师和 名女教师(记男教师为
名女教师(记男教师为 ,两名女教师为
,两名女教师为 、
、 ).
).(1)若从两校参加活动的教师中各任选
 名,写出所有可能的结果,并求选出的
名,写出所有可能的结果,并求选出的 名教师性别相同的概率;
名教师性别相同的概率;(2)若从报名的
 名教师中任选
名教师中任选 名,求选出的
名,求选出的 名教师来自同一学校的概率.
名教师来自同一学校的概率.
您最近一年使用:0次
2023-10-27更新
|
570次组卷
|
5卷引用:10.1.3?古典概型——课后作业(巩固版)
(已下线)10.1.3?古典概型——课后作业(巩固版)(已下线)第七章 概率章末测试--同步精品课堂(北师大版2019必修第一册)陕西省渭南市富平县蓝光中学2023-2024学年高一上学期1月期末数学试题(已下线)专题23 随机事件与概率-《重难点题型·高分突破》(人教A版2019必修第二册)吉林省长春市东北师范大学附属中学2023-2024学年高二上学期期中考试数学试题
解题方法
2 . 一个盒子中装有4个编号依次为1、2、3、4的球,这4个球除号码外完全相同,采用放回方式取球,先从盒子中随机取一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 .
.
(1)写出试验的样本空间;
(2)设事件A=“两次取出球的编号之和小于4”,事件B=“编号 ”,分别求事件A,B,AB发生的概率
”,分别求事件A,B,AB发生的概率 .
.
 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 .
.(1)写出试验的样本空间;
(2)设事件A=“两次取出球的编号之和小于4”,事件B=“编号
 ”,分别求事件A,B,AB发生的概率
”,分别求事件A,B,AB发生的概率 .
.
您最近一年使用:0次
解题方法
3 . 小军、小燕和小明是同班同学,假设他们3人早上到校先后的可能性相等,求:
(1)事件“小燕比小明先到校”的概率;
(2)事件“小燕比小明先到校,小明又比小军先到校”的概率.
(1)事件“小燕比小明先到校”的概率;
(2)事件“小燕比小明先到校,小明又比小军先到校”的概率.
您最近一年使用:0次
2023-10-09更新
|
178次组卷
|
5卷引用:2.2 古典概型的应用
(已下线)2.2 古典概型的应用北师大版(2019)必修第一册课本习题第七章2.2古典概型的应用北师大版(2019)必修第一册课本例题2.2 古典概型的应用【导学案】2.2 古典概型的应用课前预习-北师大版2019必修第一册第七章概率(已下线)【高一模块四】回归5 概率与统计的课本典型例题和习题
解题方法
4 . 袋中有2个白球和2个黑球,这4个球除颜色外完全相同,从中任意摸出2个,求至少摸出1个黑球的概率.
您最近一年使用:0次
2023-10-09更新
|
209次组卷
|
5卷引用:2.2 古典概型的应用
(已下线)2.2 古典概型的应用北师大版(2019)必修第一册课本习题第七章2.2古典概型的应用(已下线)10.1.3 古典概型(分层作业)-【上好课】(人教A版2019必修第二册)北师大版(2019)必修第一册课本例题2.2 古典概型的应用【导学案】2.2 古典概型的应用课前预习-北师大版2019必修第一册第七章概率
5 . 甲、乙两人约定玩一种游戏,把一枚均匀的骰子连续抛掷3次,游戏规则有下述3种,这3种规则是否公平?对谁更有利?为什么?
(1)若三次掷出的点数之和为奇数,则甲获胜;若三次掷出的点数之和为偶数,则乙获胜.
(2)若三次掷出的点数为一奇两偶或两奇一偶,则甲获胜;若三次掷出的点数均为奇数或均为偶数,则乙获胜.
(3)若三次掷出的点数之和为3,4,5,6,7,14,15,16,17,18其中之一,则甲获胜;否则乙获胜.
(1)若三次掷出的点数之和为奇数,则甲获胜;若三次掷出的点数之和为偶数,则乙获胜.
(2)若三次掷出的点数为一奇两偶或两奇一偶,则甲获胜;若三次掷出的点数均为奇数或均为偶数,则乙获胜.
(3)若三次掷出的点数之和为3,4,5,6,7,14,15,16,17,18其中之一,则甲获胜;否则乙获胜.
您最近一年使用:0次
解题方法
6 . 某次茶话会上,共安排4个节目,其中有2个歌唱节目、1个舞蹈节目、1个小品节目,按任意次序排出一个节目单,试求下列事件的概率:
(1)舞蹈在最前或最后;
(2)舞蹈和小品1个在最前、1个在最后;
(3)舞蹈和小品至少有1个在最前或最后;
(4)两个歌唱节目相邻;
(5)舞蹈排在小品之前.
(1)舞蹈在最前或最后;
(2)舞蹈和小品1个在最前、1个在最后;
(3)舞蹈和小品至少有1个在最前或最后;
(4)两个歌唱节目相邻;
(5)舞蹈排在小品之前.
您最近一年使用:0次
7 . 从甲、乙、丙、丁4位同学中选取2位去参与一项公益活动,试求下列事件的概率:
(1)甲被选中;
(2)丁没被选中;
(3)甲、丁至少有1人被选中.
(1)甲被选中;
(2)丁没被选中;
(3)甲、丁至少有1人被选中.
您最近一年使用:0次
解题方法
8 . 袋中装有2个白球和3个黑球,这5个球除颜色外完全相同.
(1)采取有放回抽取方式,从中依次摸出两个球,求两球颜色不同的概率;
(2)采取不放回抽取方式,从中依次摸出两个球,求两球颜色不同的概率.
(1)采取有放回抽取方式,从中依次摸出两个球,求两球颜色不同的概率;
(2)采取不放回抽取方式,从中依次摸出两个球,求两球颜色不同的概率.
您最近一年使用:0次
解题方法
9 . 将一枚均匀的硬币连续抛掷4次,设事件A表示“2次出现正面,2次出现反面”,事件B表示“3次出现正面,1次出现反面”,则事件A与事件B发生的概率哪个更大?
您最近一年使用:0次
解题方法
10 . 某山村海拔较高,交通极为不便,被称为“云端上的村庄”,系建档立卡贫困村.民政部门为此组建了精准扶贫队对该村进行定点帮扶,扶贫组在实地调研后,立足当地独特优势,大力发展乡村经济,带动全村父老乡亲脱贫奔小康.为了解贫困户的帮扶情况,该地民政部门从本村的贫困户中随机抽取100户对去年的年收入进行了一个抽样调查,得到如下表所示的频数表:
(1)估计本村的贫困户的年收入的众数、第75百分位数;
(2)用分层抽样的方法从这100户贫困户抽取20户贫困户进行帮扶,若再从抽样调查收入在 和
和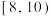 的贫困户中随机选取2户作为重点帮扶对象,求至少有一户来自收入在
的贫困户中随机选取2户作为重点帮扶对象,求至少有一户来自收入在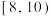 千元的概率;
千元的概率;
收入(千元) |
|
|
|
|
|
|
频数 | 15 | 10 | 35 | 20 | 10 | 10 |
(2)用分层抽样的方法从这100户贫困户抽取20户贫困户进行帮扶,若再从抽样调查收入在
 和
和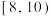 的贫困户中随机选取2户作为重点帮扶对象,求至少有一户来自收入在
的贫困户中随机选取2户作为重点帮扶对象,求至少有一户来自收入在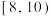 千元的概率;
千元的概率;
您最近一年使用:0次
2023-09-25更新
|
437次组卷
|
3卷引用:5.3.4 频率与概率+5.3.5 随机事件的独立性+5.4 统计与概率的应用——课后作业(基础版)
(已下线)5.3.4 频率与概率+5.3.5 随机事件的独立性+5.4 统计与概率的应用——课后作业(基础版)浙江省衢温“5+1”联盟2022-2023学年高二上学期期中联考数学试题四川省成都市2023-2024学年高二上学期九月调研考试(校级联考)数学试题