解题方法
1 . 为普及传染病防治知识,增强学生的疾病防范意识,提高自身保护能力,校委会在全校学生范围内,组织了一次传染病及个人卫生相关知识有奖竞赛(满分100分),竞赛奖励规则如下:得分在 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在 内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.
内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.
(1)从该样本中随机抽取2名学生的竞赛成绩,求这2名学生恰有一名学生获奖的概率;
(2)若该校所有参赛学生的成绩X近似地服从正态分布 ,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为
,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在 内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.
内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.| 竞赛成绩 | 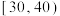 | 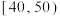 |  |  |  |  |  |
| 人数 | 6 | 12 | 18 | 34 | 16 | 8 | 6 |
(2)若该校所有参赛学生的成绩X近似地服从正态分布
 ,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为
,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
名校
2 . 九连环是中国传统的有代表性的智力玩具,凝结着中国传统文化,具有极强的趣味性九连环既能练脑又能练手,对开发人的逻辑思维能力及活动手指筋骨大有好处.同时它还可以培养学习工作的专注精神和耐心,实为老少咸宜.据明代杨慎《丹铅总录》记载,曾以玉石为材料制成两个互贯的圆环,“两环互相贯为一,得其关换,解之为二,又合而为一”.后来,以铜或铁代替玉石.甲、乙两位同学进行九连环比赛,每局不存在平局.比赛规则规定,领先3局者获胜.若比赛进行了7局,仍然没有人领先3局,比赛结束,领先者也获胜.已知甲同学每局获胜的概率为 ,且每局之间相互独立.现比赛已经进行了2局,甲同学2局全输.
,且每局之间相互独立.现比赛已经进行了2局,甲同学2局全输.
(1)由于某种原因,比赛规则改为“五局三胜制”,试判断新规则对谁更有利,并说明理由;
(2)设比赛总局数为 ,求随机变量
,求随机变量 的分布列及期望.
的分布列及期望.
 ,且每局之间相互独立.现比赛已经进行了2局,甲同学2局全输.
,且每局之间相互独立.现比赛已经进行了2局,甲同学2局全输.(1)由于某种原因,比赛规则改为“五局三胜制”,试判断新规则对谁更有利,并说明理由;
(2)设比赛总局数为
 ,求随机变量
,求随机变量 的分布列及期望.
的分布列及期望.
您最近一年使用:0次
2022-06-07更新
|
1078次组卷
|
3卷引用:福建省厦门外国语学校2021-2022学年高二下学期数学期末模拟试题(4)



