名校
解题方法
1 . 对于椭圆 ,令
,令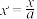 ,
, ,那么在坐标系
,那么在坐标系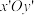 中,椭圆经伸缩变换得到了单位圆
中,椭圆经伸缩变换得到了单位圆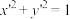 ,在这样的伸缩变换中,有些几何关系保持不变,例如点、直线、曲线的位置关系以及点分线段的比等等;而有些几何量则等比例变化,例如任何封闭图形在变换后的面积变为原先的
,在这样的伸缩变换中,有些几何关系保持不变,例如点、直线、曲线的位置关系以及点分线段的比等等;而有些几何量则等比例变化,例如任何封闭图形在变换后的面积变为原先的 ,由此我们可以借助圆的几何性质处理一些椭圆的问题.
,由此我们可以借助圆的几何性质处理一些椭圆的问题.
(1)在原坐标系中斜率为k的直线l,经过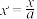 ,
, 的伸缩变换后斜率变为
的伸缩变换后斜率变为 ,求k与
,求k与 满足的关系;
满足的关系;
(2)设动点P在椭圆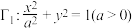 上,过点P作椭圆
上,过点P作椭圆 的切线,与椭圆
的切线,与椭圆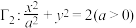 交于点Q,R,再过点Q,R分别作椭圆
交于点Q,R,再过点Q,R分别作椭圆 的切线交于点S,求点S的轨迹方程;
的切线交于点S,求点S的轨迹方程;
(3)点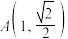 )在椭圆
)在椭圆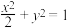 上,求椭圆上点B,C的坐标,使得△ABC的面积取最大值,并求出该最大值.
上,求椭圆上点B,C的坐标,使得△ABC的面积取最大值,并求出该最大值.
 ,令
,令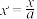 ,
, ,那么在坐标系
,那么在坐标系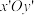 中,椭圆经伸缩变换得到了单位圆
中,椭圆经伸缩变换得到了单位圆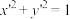 ,在这样的伸缩变换中,有些几何关系保持不变,例如点、直线、曲线的位置关系以及点分线段的比等等;而有些几何量则等比例变化,例如任何封闭图形在变换后的面积变为原先的
,在这样的伸缩变换中,有些几何关系保持不变,例如点、直线、曲线的位置关系以及点分线段的比等等;而有些几何量则等比例变化,例如任何封闭图形在变换后的面积变为原先的 ,由此我们可以借助圆的几何性质处理一些椭圆的问题.
,由此我们可以借助圆的几何性质处理一些椭圆的问题.(1)在原坐标系中斜率为k的直线l,经过
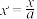 ,
, 的伸缩变换后斜率变为
的伸缩变换后斜率变为 ,求k与
,求k与 满足的关系;
满足的关系;(2)设动点P在椭圆
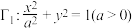 上,过点P作椭圆
上,过点P作椭圆 的切线,与椭圆
的切线,与椭圆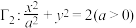 交于点Q,R,再过点Q,R分别作椭圆
交于点Q,R,再过点Q,R分别作椭圆 的切线交于点S,求点S的轨迹方程;
的切线交于点S,求点S的轨迹方程;(3)点
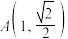 )在椭圆
)在椭圆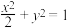 上,求椭圆上点B,C的坐标,使得△ABC的面积取最大值,并求出该最大值.
上,求椭圆上点B,C的坐标,使得△ABC的面积取最大值,并求出该最大值.
您最近一年使用:0次



