1 . 已知集合A为非空数集.定义:
(1)若集合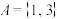 ,直接写出集合S,T;
,直接写出集合S,T;
(2)若集合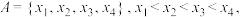 且
且 .求证:
.求证: ;
;
(3)若集合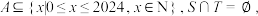 记
记 为集合A中元素的个数,求
为集合A中元素的个数,求 的最大值.
的最大值.

(1)若集合
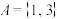 ,直接写出集合S,T;
,直接写出集合S,T;(2)若集合
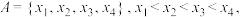 且
且 .求证:
.求证: ;
;(3)若集合
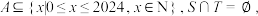 记
记 为集合A中元素的个数,求
为集合A中元素的个数,求 的最大值.
的最大值.
您最近半年使用:0次
名校
2 . 已知集合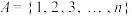 ,其中
,其中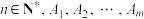 都是
都是 的子集且互不相同,记
的子集且互不相同,记 的元素个数,
的元素个数,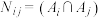 的元素个数
的元素个数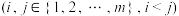 .
.
(1)若 ,直接写出所有满足条件的集合
,直接写出所有满足条件的集合 ;
;
(2)若 ,且对任意
,且对任意 ,都有
,都有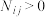 ,求
,求 的最大值;
的最大值;
(3)若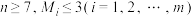 且对任意
且对任意 ,都有
,都有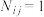 ,求
,求 的最大值.
的最大值.
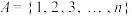 ,其中
,其中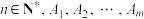 都是
都是 的子集且互不相同,记
的子集且互不相同,记 的元素个数,
的元素个数,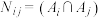 的元素个数
的元素个数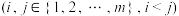 .
.(1)若
 ,直接写出所有满足条件的集合
,直接写出所有满足条件的集合 ;
;(2)若
 ,且对任意
,且对任意 ,都有
,都有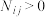 ,求
,求 的最大值;
的最大值;(3)若
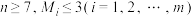 且对任意
且对任意 ,都有
,都有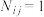 ,求
,求 的最大值.
的最大值.
您最近半年使用:0次
2024-03-23更新
|
601次组卷
|
2卷引用:北京市北师大附属实验中学2024届高三下学期3月零模数学试题
3 . 群的概念由法国天才数学家伽罗瓦(1811-1832)在19世纪30年代开创,群论虽起源于对代数多项式方程的研究,但在量子力学、晶体结构学等其他学科中也有十分广泛的应用.设 是一个非空集合,“
是一个非空集合,“ ”是一个适用于
”是一个适用于 中元素的运算,若同时满足以下四个条件,则称
中元素的运算,若同时满足以下四个条件,则称 对“
对“ ”构成一个群:(1)封闭性,即若
”构成一个群:(1)封闭性,即若 ,则存在唯一确定的
,则存在唯一确定的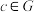 ,使得
,使得 ;(2)结合律成立,即对
;(2)结合律成立,即对 中任意元素
中任意元素 都有
都有 ;(3)单位元存在,即存在
;(3)单位元存在,即存在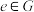 ,对任意
,对任意 ,满足
,满足 ,则
,则 称为单位元;(4)逆元存在,即任意
称为单位元;(4)逆元存在,即任意 ,存在
,存在 ,使得
,使得 ,则称
,则称 与
与 互为逆元,
互为逆元, 记作
记作 .一般地,
.一般地, 可简记作
可简记作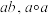 可简记作
可简记作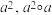 可简记作
可简记作 ,以此类推.正八边形
,以此类推.正八边形 的中心为
的中心为 .以
.以 表示恒等变换,即不对正八边形作任何变换;以
表示恒等变换,即不对正八边形作任何变换;以 表示以点
表示以点 为中心,将正八边形逆时针旋转
为中心,将正八边形逆时针旋转 的旋转变换;以
的旋转变换;以 表示以
表示以 所在直线为轴,将正八边形进行轴对称变换.定义运算“
所在直线为轴,将正八边形进行轴对称变换.定义运算“ ”表示复合变换,即
”表示复合变换,即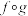 表示将正八边形先进行
表示将正八边形先进行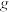 变换再进行
变换再进行 变换的变换.以形如
变换的变换.以形如 ,并规定
,并规定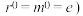 的变换为元素,可组成集合
的变换为元素,可组成集合 ,则
,则 对运算“
对运算“ ”可构成群,称之为“正八边形的对称变换群”,记作
”可构成群,称之为“正八边形的对称变换群”,记作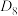 .则以下关于
.则以下关于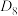 及其元素的说法中,正确的有( )
及其元素的说法中,正确的有( )
 是一个非空集合,“
是一个非空集合,“ ”是一个适用于
”是一个适用于 中元素的运算,若同时满足以下四个条件,则称
中元素的运算,若同时满足以下四个条件,则称 对“
对“ ”构成一个群:(1)封闭性,即若
”构成一个群:(1)封闭性,即若 ,则存在唯一确定的
,则存在唯一确定的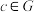 ,使得
,使得 ;(2)结合律成立,即对
;(2)结合律成立,即对 中任意元素
中任意元素 都有
都有 ;(3)单位元存在,即存在
;(3)单位元存在,即存在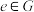 ,对任意
,对任意 ,满足
,满足 ,则
,则 称为单位元;(4)逆元存在,即任意
称为单位元;(4)逆元存在,即任意 ,存在
,存在 ,使得
,使得 ,则称
,则称 与
与 互为逆元,
互为逆元, 记作
记作 .一般地,
.一般地, 可简记作
可简记作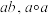 可简记作
可简记作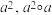 可简记作
可简记作 ,以此类推.正八边形
,以此类推.正八边形 的中心为
的中心为 .以
.以 表示恒等变换,即不对正八边形作任何变换;以
表示恒等变换,即不对正八边形作任何变换;以 表示以点
表示以点 为中心,将正八边形逆时针旋转
为中心,将正八边形逆时针旋转 的旋转变换;以
的旋转变换;以 表示以
表示以 所在直线为轴,将正八边形进行轴对称变换.定义运算“
所在直线为轴,将正八边形进行轴对称变换.定义运算“ ”表示复合变换,即
”表示复合变换,即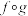 表示将正八边形先进行
表示将正八边形先进行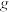 变换再进行
变换再进行 变换的变换.以形如
变换的变换.以形如 ,并规定
,并规定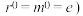 的变换为元素,可组成集合
的变换为元素,可组成集合 ,则
,则 对运算“
对运算“ ”可构成群,称之为“正八边形的对称变换群”,记作
”可构成群,称之为“正八边形的对称变换群”,记作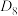 .则以下关于
.则以下关于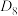 及其元素的说法中,正确的有( )
及其元素的说法中,正确的有( )A.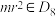 ,且 ,且 |
B. 与 与 互为逆元 互为逆元 |
C.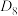 中有无穷多个元素 中有无穷多个元素 |
D.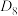 中至少存在三个不同的元素,它们的逆元都是其本身 中至少存在三个不同的元素,它们的逆元都是其本身 |
您最近半年使用:0次
名校
解题方法
4 . 设集合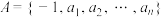 ,其中
,其中 .若对任意的向量
.若对任意的向量 ,存在向量
,存在向量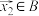 ,使得
,使得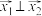 ,则称A是“T集”.
,则称A是“T集”.
(1)设 ,判断M,N是否为“T集”.若不是,请说明理由;
,判断M,N是否为“T集”.若不是,请说明理由;
(2)已知A是“T集”.
(i)若A中的元素由小到大排列成等差数列,求A;
(ii)若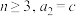 (c为常数),求有穷数列
(c为常数),求有穷数列 的通项公式.
的通项公式.
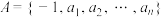 ,其中
,其中 .若对任意的向量
.若对任意的向量 ,存在向量
,存在向量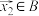 ,使得
,使得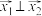 ,则称A是“T集”.
,则称A是“T集”.(1)设
 ,判断M,N是否为“T集”.若不是,请说明理由;
,判断M,N是否为“T集”.若不是,请说明理由;(2)已知A是“T集”.
(i)若A中的元素由小到大排列成等差数列,求A;
(ii)若
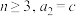 (c为常数),求有穷数列
(c为常数),求有穷数列 的通项公式.
的通项公式.
您最近半年使用:0次
2024-03-20更新
|
897次组卷
|
3卷引用:江苏省南通市海安高级中学2024届高三下学期开学考试数学试题
5 . 将2024表示成5个正整数 ,
, ,
, ,
, ,
,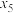 之和,得到方程
之和,得到方程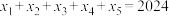 ①,称五元有序数组
①,称五元有序数组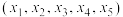 为方程①的解,对于上述的五元有序数组
为方程①的解,对于上述的五元有序数组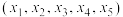 ,当
,当 时,若
时,若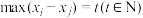 ,则称
,则称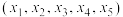 是
是 密集的一组解.
密集的一组解.
(1)方程①是否存在一组解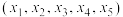 ,使得
,使得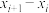
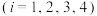 等于同一常数?若存在,请求出该常数;若不存在,请说明理由;
等于同一常数?若存在,请求出该常数;若不存在,请说明理由;
(2)方程①的解中共有多少组是 密集的?
密集的?
(3)记 ,问
,问 是否存在最小值?若存在,请求出
是否存在最小值?若存在,请求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
 ,
, ,
, ,
, ,
,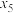 之和,得到方程
之和,得到方程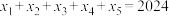 ①,称五元有序数组
①,称五元有序数组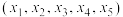 为方程①的解,对于上述的五元有序数组
为方程①的解,对于上述的五元有序数组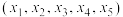 ,当
,当 时,若
时,若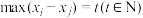 ,则称
,则称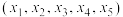 是
是 密集的一组解.
密集的一组解.(1)方程①是否存在一组解
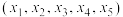 ,使得
,使得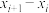
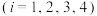 等于同一常数?若存在,请求出该常数;若不存在,请说明理由;
等于同一常数?若存在,请求出该常数;若不存在,请说明理由;(2)方程①的解中共有多少组是
 密集的?
密集的?(3)记
 ,问
,问 是否存在最小值?若存在,请求出
是否存在最小值?若存在,请求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
您最近半年使用:0次
2024-03-18更新
|
1086次组卷
|
2卷引用:广东省江门市2024届高三一模考试数学试卷
2024高三·江苏·专题练习
6 . 定义集合运算: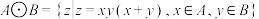 ,集合
,集合 ,则集合
,则集合 所有元素之和为
所有元素之和为______ .
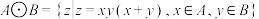 ,集合
,集合 ,则集合
,则集合 所有元素之和为
所有元素之和为
您最近半年使用:0次
7 . 由无理数引发的数学危机一直延续到19世纪,直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集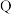 划分为两个非空的子集M与N,且满足
划分为两个非空的子集M与N,且满足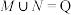 ,
,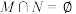 ,M中的每一个元素小于
,M中的每一个元素小于 中的每一个元素,则称
中的每一个元素,则称 为戴德金分割.试判断下列选项中,可能成立的是( )
为戴德金分割.试判断下列选项中,可能成立的是( )
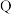 划分为两个非空的子集M与N,且满足
划分为两个非空的子集M与N,且满足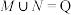 ,
,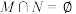 ,M中的每一个元素小于
,M中的每一个元素小于 中的每一个元素,则称
中的每一个元素,则称 为戴德金分割.试判断下列选项中,可能成立的是( )
为戴德金分割.试判断下列选项中,可能成立的是( )A.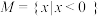 , ,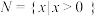 是一个戴德金分割 是一个戴德金分割 |
| B.M没有最大元素,N有一个最小元素 |
| C.M有一个最大元素,N有一个最小元素 |
| D.M没有最大元素,N也没有最小元素 |
您最近半年使用:0次
8 . 在正方形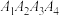 中,设D是正方形
中,设D是正方形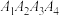 的内部的点构成的集合,
的内部的点构成的集合, ,则集合
,则集合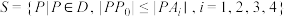 表示的平面区域可能是( )
表示的平面区域可能是( )
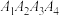 中,设D是正方形
中,设D是正方形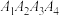 的内部的点构成的集合,
的内部的点构成的集合, ,则集合
,则集合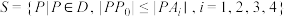 表示的平面区域可能是( )
表示的平面区域可能是( )| A.四边形区域 | B.五边形区域 | C.六边形区域 | D.八边形区域 |
您最近半年使用:0次
名校
9 . 设A是正整数集的一个非空子集,如果对于任意 ,都有
,都有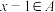 或
或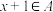 ,则称A为自邻集.记集合
,则称A为自邻集.记集合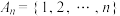
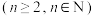 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.
(1)直接写出 的所有自邻集;
的所有自邻集;
(2)若n为偶数且 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;
(3)若 ,求证:
,求证: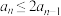 .
.
 ,都有
,都有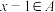 或
或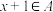 ,则称A为自邻集.记集合
,则称A为自邻集.记集合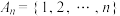
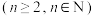 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.(1)直接写出
 的所有自邻集;
的所有自邻集;(2)若n为偶数且
 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;(3)若
 ,求证:
,求证: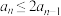 .
.
您最近半年使用:0次
10 . 拓扑学是一个研究图形(或集合)整体结构和性质的一门几何学,以抽象而严谨的语言将几何与集合联系起来,富有直观和逻辑.已知平面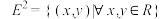 ,定义对
,定义对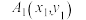 ,
,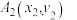 ,其度量(距离)
,其度量(距离) 并称
并称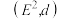 为一度量平面.设
为一度量平面.设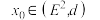 ,
,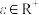 ,称平面区域
,称平面区域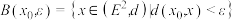 为以
为以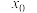 为心,
为心,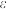 为半径的球形邻域.
为半径的球形邻域.
(1)试用集合语言描述两个球形邻域的交集;
(2)证明: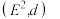 中的任意两个球形邻域的交集是若干个球形邻域的并集;
中的任意两个球形邻域的交集是若干个球形邻域的并集;
(3)一个集合称作“开集”当且仅当其是一个无边界的点集.证明: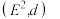 的一个子集是开集当且仅当其可被表示为若干个球形邻域的并集.
的一个子集是开集当且仅当其可被表示为若干个球形邻域的并集.
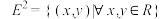 ,定义对
,定义对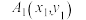 ,
,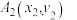 ,其度量(距离)
,其度量(距离) 并称
并称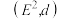 为一度量平面.设
为一度量平面.设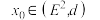 ,
,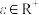 ,称平面区域
,称平面区域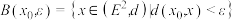 为以
为以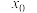 为心,
为心,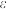 为半径的球形邻域.
为半径的球形邻域.(1)试用集合语言描述两个球形邻域的交集;
(2)证明:
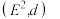 中的任意两个球形邻域的交集是若干个球形邻域的并集;
中的任意两个球形邻域的交集是若干个球形邻域的并集;(3)一个集合称作“开集”当且仅当其是一个无边界的点集.证明:
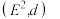 的一个子集是开集当且仅当其可被表示为若干个球形邻域的并集.
的一个子集是开集当且仅当其可被表示为若干个球形邻域的并集.
您最近半年使用:0次



