名校
1 . 如图,已知矩形 的对角线交于点
的对角线交于点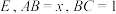 ,将
,将 沿
沿 翻折,若在翻折过程中存在某个位置,使得
翻折,若在翻折过程中存在某个位置,使得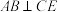 ,则
,则 的取值范围是( )
的取值范围是( )

 的对角线交于点
的对角线交于点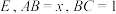 ,将
,将 沿
沿 翻折,若在翻折过程中存在某个位置,使得
翻折,若在翻折过程中存在某个位置,使得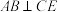 ,则
,则 的取值范围是( )
的取值范围是( )
A.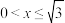 | B. |
C.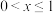 | D.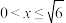 |
您最近一年使用:0次
2022-05-26更新
|
2056次组卷
|
6卷引用:浙江省杭州高级中学2022届高三下学期5月仿真模拟数学试题
浙江省杭州高级中学2022届高三下学期5月仿真模拟数学试题浙江省金华十校2021-2022学年高一下学期期末模拟数学试题(已下线)第30练 空间向量的应用(已下线)专题16 空间向量及其应用(模拟练)(已下线)专题07 立体几何小题常考全归类(精讲精练)-2浙江省绍兴市鲁迅中学2022-2023学年高二普通班上学期期末模拟数学试题
名校
2 . 如图,在三棱锥 中,
中, ,
,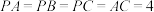 ,
, 为
为 中点.
中点.

(1)证明: 平面
平面 ;
;
(2)若点 在棱
在棱 上,
上,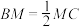 ,且
,且 ,求二面角
,求二面角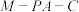 的大小.
的大小.
 中,
中, ,
,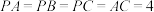 ,
, 为
为 中点.
中点.
(1)证明:
 平面
平面 ;
;(2)若点
 在棱
在棱 上,
上,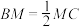 ,且
,且 ,求二面角
,求二面角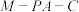 的大小.
的大小.
您最近一年使用:0次
2022-05-11更新
|
1755次组卷
|
5卷引用:宁夏石嘴山市第一中学2022届高三下学期第三次模拟数学(理)考试题
名校
3 . 如图①,在梯形ABCD中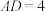 ,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.

(1)求证:OC⊥平面PBE;
(2)求直线PB与平面PCD所成角的正弦值.
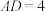 ,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
(1)求证:OC⊥平面PBE;
(2)求直线PB与平面PCD所成角的正弦值.
您最近一年使用:0次
2022-05-10更新
|
782次组卷
|
3卷引用:陕西省西安市周至县2022届高三下学期三模理科数学试题
名校
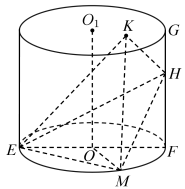
4 . 如图所示,圆柱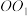 中,
中, 是底面直径,点
是底面直径,点 是
是 上一点,
上一点,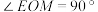 ,点
,点 是母线
是母线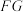 上一点,点
上一点,点 是上底面的一动点,
是上底面的一动点,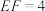 ,
,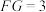 ,
,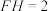 ,则( )
,则( )
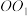 中,
中, 是底面直径,点
是底面直径,点 是
是 上一点,
上一点,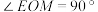 ,点
,点 是母线
是母线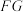 上一点,点
上一点,点 是上底面的一动点,
是上底面的一动点,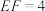 ,
,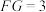 ,
,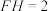 ,则( )
,则( )
A.存在点 ,使得 ,使得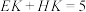 |
B.存在唯一的点 ,使得 ,使得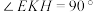 |
C.满足 的点 的点 的轨迹长度是 的轨迹长度是 |
D.当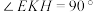 时,三棱锥 时,三棱锥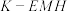 外接球的表面积是 外接球的表面积是 |
您最近一年使用:0次
2022-05-08更新
|
591次组卷
|
3卷引用:安徽省芜湖市2022届高三下学期5月教育教学质量监控理科数学试题
名校
解题方法
5 . 在所有棱长都相等的正三棱柱中,点A是三棱柱的顶点,M,N、Q是所在棱的中点,则下列选项中直线AQ与直线MN垂直的是( )
A.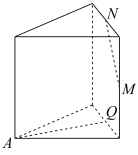 | B. | C.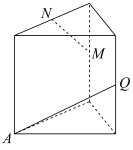 | D.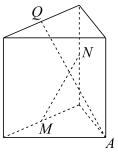 |
您最近一年使用:0次
2022-05-02更新
|
2033次组卷
|
5卷引用:广东省2022届高三二模数学试题
广东省2022届高三二模数学试题湖南省长沙市长郡中学2022届高三下学期高考前保温卷数学试题(已下线)第12练 空间直线、平面的垂直-2022年【暑假分层作业】高一数学(人教A版2019必修第二册)(已下线)第05讲 空间向量及其应用(练)福建省厦门双十中学2023届高三上学期第三次月考数学试题
名校
解题方法
6 . 正方体 的棱长为
的棱长为 ,
, 分别为
分别为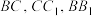 的中点,动点
的中点,动点 在线段
在线段 上,则下列结论中正确的是( )
上,则下列结论中正确的是( )
 的棱长为
的棱长为 ,
,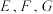 分别为
分别为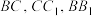 的中点,动点
的中点,动点 在线段
在线段 上,则下列结论中正确的是( )
上,则下列结论中正确的是( )A.直线 与直线 与直线 异面 异面 | B.平面 截正方体所得的截面面积为 截正方体所得的截面面积为 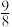 |
C.存在点 ,使得平面 ,使得平面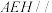 平面 平面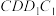 | D.三棱锥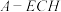 的体积为定值 的体积为定值 |
您最近一年使用:0次
2022-04-29更新
|
1022次组卷
|
4卷引用:湖北省襄阳市第五中学2022届高三下学期适应性考试(四)数学试题
湖北省襄阳市第五中学2022届高三下学期适应性考试(四)数学试题云南省曲靖市2023届高三第二次教学质量监测数学试题山西省长治市第二中学校2021-2022学年高一下学期期中数学试题(已下线)专题08 立体几何综合-备战2023年高考数学母题题源解密(新高考卷)
7 . 在正四棱柱 中,
中,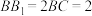 ,
, 为
为 的中点,点
的中点,点 为线段
为线段 上的动点,则三棱锥
上的动点,则三棱锥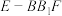 的外接球表面积的最大值为( )
的外接球表面积的最大值为( )
 中,
中,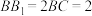 ,
, 为
为 的中点,点
的中点,点 为线段
为线段 上的动点,则三棱锥
上的动点,则三棱锥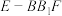 的外接球表面积的最大值为( )
的外接球表面积的最大值为( )A. | B. | C.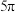 | D. |
您最近一年使用:0次
名校
解题方法
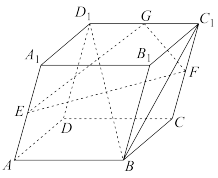
8 . 如图,已知四棱柱 的底面为平行四边形,E,F,G分别为棱
的底面为平行四边形,E,F,G分别为棱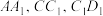 的中点,则( )
的中点,则( )
 的底面为平行四边形,E,F,G分别为棱
的底面为平行四边形,E,F,G分别为棱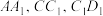 的中点,则( )
的中点,则( )
A.直线 都与平面 都与平面 平行 平行 |
B.直线 都与平面 都与平面 相交 相交 |
C.直线 与平面 与平面 平行,直线 平行,直线 与平面 与平面 相交 相交 |
D.直线 与平面 与平面 相交,直线 相交,直线 与平面 与平面 平行 平行 |
您最近一年使用:0次
2022-04-20更新
|
1050次组卷
|
11卷引用:陕西省西安中学2022届高三下学期三模文科数学试题
陕西省西安中学2022届高三下学期三模文科数学试题八省八校(T8联考)2022届高三上学期第一次联考数学试题(已下线)数学-2022届高三下学期开学摸底考试卷C(新高考专用)(已下线)第八章 立体几何初步(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(人教A版2019必修第二册)江西师范大学附属中学2021-2022学年高二下学期第一次月考数学(理)试题(已下线)第24讲 空间直线、平面的平行的基本概念专题6.5 立体几何初步(基础巩固卷)-2021-2022学年高一数学北师大版2019必修第二册华师一附中等T8联考2021-2022学年高三上学期第一次联考数学试题四川省遂宁市绿然教科院2021-2022学年高二上学期期末联考文科数学试题四川省遂宁市绿然教科院2021-2022学年高二上学期期末联考数学(理)试题内蒙古赤峰市赤峰二中2024届高三上学期12月月考数学(理)试题
9 . 如图,已知正方体 棱长为4,Q是
棱长为4,Q是 上一动点,点H在棱
上一动点,点H在棱 上,且
上,且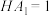 ,在侧面
,在侧面 内作边长为1的正方形
内作边长为1的正方形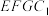 ,P是侧面
,P是侧面 内一动点,且点P到平面
内一动点,且点P到平面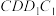 距离等于线段
距离等于线段 的长,下列说法正确的是( )
的长,下列说法正确的是( )
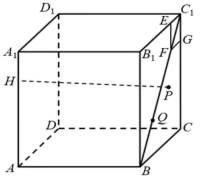
 棱长为4,Q是
棱长为4,Q是 上一动点,点H在棱
上一动点,点H在棱 上,且
上,且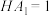 ,在侧面
,在侧面 内作边长为1的正方形
内作边长为1的正方形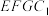 ,P是侧面
,P是侧面 内一动点,且点P到平面
内一动点,且点P到平面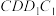 距离等于线段
距离等于线段 的长,下列说法正确的是( )
的长,下列说法正确的是( )
A.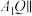 平面 平面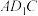 |
B.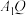 与平面 与平面 所成角的正切值得最大值为 所成角的正切值得最大值为 |
C.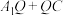 的最小值为 的最小值为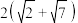 |
D.当点P运动时,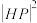 的范围是 的范围是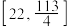 |
您最近一年使用:0次
2022-04-19更新
|
782次组卷
|
3卷引用:广东省揭阳市普宁国贤学校2023届高三下学期模拟数学试题
名校
10 . 如图,在棱长为1的正方体ABCD—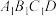 中,E为侧面
中,E为侧面 的中心,F是棱
的中心,F是棱 的中点,若点P为线段
的中点,若点P为线段 上的动点,N为ABCD所在平面内的动点,则下列说法正确的是( )
上的动点,N为ABCD所在平面内的动点,则下列说法正确的是( )
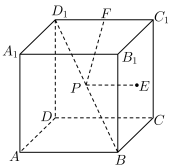
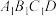 中,E为侧面
中,E为侧面 的中心,F是棱
的中心,F是棱 的中点,若点P为线段
的中点,若点P为线段 上的动点,N为ABCD所在平面内的动点,则下列说法正确的是( )
上的动点,N为ABCD所在平面内的动点,则下列说法正确的是( )
A. · ·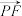 的最小值为 的最小值为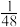 |
B.若 ,则平面PAC截正方体所得截面的面积为 ,则平面PAC截正方体所得截面的面积为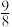 |
C.若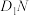 与AB所成的角为 与AB所成的角为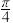 ,则N点的轨迹为双曲线 ,则N点的轨迹为双曲线 |
D.若正方体绕 旋转θ角度后与其自身重合,则θ的最小值是 旋转θ角度后与其自身重合,则θ的最小值是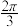 |
您最近一年使用:0次
2022-03-19更新
|
1700次组卷
|
6卷引用:湖北省襄阳市第五中学2022届高三下学期适应性考试(一)数学试题
湖北省襄阳市第五中学2022届高三下学期适应性考试(一)数学试题江苏省南京市金陵中学2021-2022学年高二下学期第一次阶段检测数学试题福建省厦门外国语学校2021-2022学年高二下学期第一次月考数学试题(已下线)专题22 立体几何中的轨迹问题-2广东省四校2023届高三上学期第一次联考数学试题(已下线)专题1.13 空间向量与立体几何全章综合测试卷-提高篇-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)



