名校
1 . 已知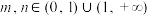 ,若
,若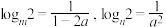 ,则下列命题正确的是( )
,则下列命题正确的是( )
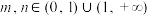 ,若
,若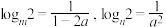 ,则下列命题正确的是( )
,则下列命题正确的是( )A.若 ,则 ,则 | B.若 ,则 ,则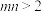 |
C.若 ,则 ,则 | D.若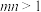 ,则 ,则 |
您最近一年使用:0次
2024-10-14更新
|
393次组卷
|
2卷引用:安徽省皖豫名校联盟2025届高三上学期10月联考数学试题
2 . 某工厂产生的废气经过滤后排放,过滤过程中废气的污染物含量 (单位:
(单位: 与时间
与时间 (单位:h)之间的关系式为
(单位:h)之间的关系式为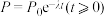 ,其中
,其中 为初始污染物含量,
为初始污染物含量,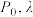 均为正的常数,已知过滤前后废气的体积相等,且在前4h过滤掉了
均为正的常数,已知过滤前后废气的体积相等,且在前4h过滤掉了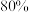 的污染物.如果废气中污染物的含量不超过
的污染物.如果废气中污染物的含量不超过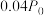 时达到排放标准,那么该工厂产生的废气要达到排放标准,至少需要过滤的时间为( )
时达到排放标准,那么该工厂产生的废气要达到排放标准,至少需要过滤的时间为( )
 (单位:
(单位: 与时间
与时间 (单位:h)之间的关系式为
(单位:h)之间的关系式为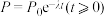 ,其中
,其中 为初始污染物含量,
为初始污染物含量,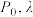 均为正的常数,已知过滤前后废气的体积相等,且在前4h过滤掉了
均为正的常数,已知过滤前后废气的体积相等,且在前4h过滤掉了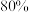 的污染物.如果废气中污染物的含量不超过
的污染物.如果废气中污染物的含量不超过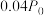 时达到排放标准,那么该工厂产生的废气要达到排放标准,至少需要过滤的时间为( )
时达到排放标准,那么该工厂产生的废气要达到排放标准,至少需要过滤的时间为( )| A.4h | B.6h | C.8h | D.12h |
您最近一年使用:0次
解题方法
3 . (1)已知函数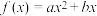 满足
满足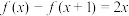 ,求
,求 在区间
在区间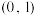 上的值域;
上的值域;
(2)若函数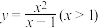 的最小值为
的最小值为 ,且
,且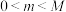 ,求
,求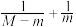 的最小值.
的最小值.
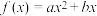 满足
满足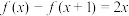 ,求
,求 在区间
在区间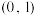 上的值域;
上的值域;(2)若函数
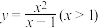 的最小值为
的最小值为 ,且
,且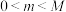 ,求
,求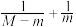 的最小值.
的最小值.
您最近一年使用:0次
4 . 设 是函数
是函数 的导函数,
的导函数, 是函数
是函数 的导函数,若方程
的导函数,若方程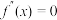 有实数解
有实数解 ,则称点
,则称点 为曲线
为曲线 的“拐点”.经过探究发现:任何一个三次函数的图象都有“拐点”,且“拐点”就是三次函数图象的对称中心.已知函数
的“拐点”.经过探究发现:任何一个三次函数的图象都有“拐点”,且“拐点”就是三次函数图象的对称中心.已知函数 13的图象的对称中心为
13的图象的对称中心为 .
.
(1)求实数m,n的值;
(2)求 的零点个数.
的零点个数.
 是函数
是函数 的导函数,
的导函数, 是函数
是函数 的导函数,若方程
的导函数,若方程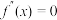 有实数解
有实数解 ,则称点
,则称点 为曲线
为曲线 的“拐点”.经过探究发现:任何一个三次函数的图象都有“拐点”,且“拐点”就是三次函数图象的对称中心.已知函数
的“拐点”.经过探究发现:任何一个三次函数的图象都有“拐点”,且“拐点”就是三次函数图象的对称中心.已知函数 13的图象的对称中心为
13的图象的对称中心为 .
.(1)求实数m,n的值;
(2)求
 的零点个数.
的零点个数.
您最近一年使用:0次
解题方法
5 . 已知函数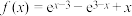 ,则满足
,则满足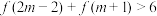 的
的 的取值范围是( )
的取值范围是( )
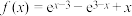 ,则满足
,则满足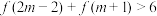 的
的 的取值范围是( )
的取值范围是( )A. | B.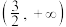 |
C. | D.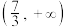 |
您最近一年使用:0次
解题方法
6 . 已知函数 .
.
(1)若 ,证明:
,证明: ;
;
(2)若 且存在
且存在 ,使得
,使得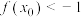 成立,求
成立,求 的取值范围.
的取值范围.
 .
.(1)若
 ,证明:
,证明: ;
;(2)若
 且存在
且存在 ,使得
,使得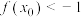 成立,求
成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
7 . 有4名志愿者参加社区服务,服务星期六、星期日两天.若每天从4人中任选两人参加服务,则恰有1人连续参加两天服务的概率为( )
A. | B. | C. | D. |
您最近一年使用:0次
2024-09-18更新
|
1062次组卷
|
4卷引用:安徽省六校2025届高三上学期第一次阶段联合教学质量测评数学试卷
安徽省六校2025届高三上学期第一次阶段联合教学质量测评数学试卷四川省巴中市2025届高三上学期“零诊”考试数学试题(已下线)第05讲 古典概型与概率的基本性质(八大题型)(练习)(已下线)周测20 排列组合与二项式定理 (高三一轮好卷提升卷)
名校
解题方法
8 . 已知函数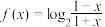 .
.
(1)判断并证明 的奇偶性;
的奇偶性;
(2)若对任意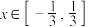 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
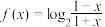 .
.(1)判断并证明
 的奇偶性;
的奇偶性;(2)若对任意
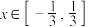 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
2024-09-12更新
|
2255次组卷
|
5卷引用:安徽省六安第二中学2024-2025学年高三上学期第二次月考(10月)数学试题
安徽省六安第二中学2024-2025学年高三上学期第二次月考(10月)数学试题重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题山东省聊城第一中学2025届高三上学期第一次月考数学试题江苏省南通市2025届高三九月份调研考试数学试题(已下线)4.2.3 对数函数的性质与图象+4.3 指数函数与对数函数的关系——课后作业(提升版)
名校
9 . 如图,在平面四边形 中,
中,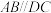 ,
, 是边长为2的正三角形,
是边长为2的正三角形, 为
为 的中点,将
的中点,将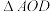 沿
沿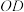 折到
折到 的位置,
的位置,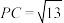 .
. ;
;
(2)若 为
为 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,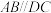 ,
, 是边长为2的正三角形,
是边长为2的正三角形, 为
为 的中点,将
的中点,将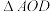 沿
沿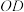 折到
折到 的位置,
的位置,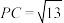 .
.
 ;
;(2)若
 为
为 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-09-04更新
|
1440次组卷
|
4卷引用:安徽省阜阳市红旗中学2024-2025学年高二上学期第一次月考(10月)数学试题
安徽省阜阳市红旗中学2024-2025学年高二上学期第一次月考(10月)数学试题吉林省长春市长春汽车经济技术开发区第三中学2025届高三上学期9月月考数学试题黑龙江省大庆市2025届高三上学期第一次质量检测数学试题(已下线)阶段测6周测14-周测18【实战演练】复盘卷(针对提升卷)
名校
解题方法
10 . 函数 是定义在R上的偶函数,且
是定义在R上的偶函数,且 ,若
,若 ,
, ,则
,则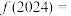 ( )
( )
 是定义在R上的偶函数,且
是定义在R上的偶函数,且 ,若
,若 ,
, ,则
,则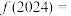 ( )
( )| A.4 | B.2 | C.1 | D.0 |
您最近一年使用:0次
2024-08-28更新
|
922次组卷
|
3卷引用:安徽省合肥市第一中学2024-2025学年高三上学期第二次素质拓展数学试题



