名校
1 . 已知函数 .
.
(1)若f(x)≤0恒成立,求m的范围?
(2)若函数y=|f(x)|在[-1,0]上是减函数,求实数m的取值范围;
(3)是否存在整数a,b,使得a≤f(x)≤b的解集恰好是[a,b],若存在,求出a,b的值;若不存在,说明理由.
 .
.(1)若f(x)≤0恒成立,求m的范围?
(2)若函数y=|f(x)|在[-1,0]上是减函数,求实数m的取值范围;
(3)是否存在整数a,b,使得a≤f(x)≤b的解集恰好是[a,b],若存在,求出a,b的值;若不存在,说明理由.
您最近一年使用:0次
名校
2 . 已知函数
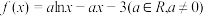 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 的图象在点
的图象在点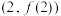 处的切线的斜率为1,问:
处的切线的斜率为1,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的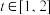 ,函数
,函数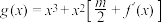 在区间
在区间 上总存在极值?
上总存在极值?

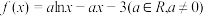 .
.(1)求函数
 的单调区间;
的单调区间;(2)若函数
 的图象在点
的图象在点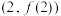 处的切线的斜率为1,问:
处的切线的斜率为1,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的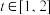 ,函数
,函数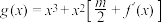 在区间
在区间 上总存在极值?
上总存在极值?
您最近一年使用:0次
2019-09-28更新
|
510次组卷
|
4卷引用:重庆市云阳江口中学2020届高三上学期第一次月考数学(文)试题
名校
解题方法
3 . 设函数 在区间
在区间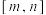 上的值域是
上的值域是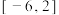 ,则
,则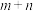 的取值的范围是
的取值的范围是______ .
 在区间
在区间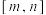 上的值域是
上的值域是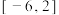 ,则
,则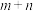 的取值的范围是
的取值的范围是
您最近一年使用:0次
2016-12-04更新
|
673次组卷
|
6卷引用:重庆市南开中学2019届高三上学期第一次月考数学(文)试题
重庆市南开中学2019届高三上学期第一次月考数学(文)试题【全国百强校】江西省宜春市上高县第二中学2019届高三上学期第一次月考数学(文)试题.广东省普宁市第二中学2021-2022学年高一上学期第二次月考数学试题2017届江西上高县二中高三上学期开学考试数学(文)试卷(已下线)《2018-2019学年同步单元双基双测AB卷》必修一 专题三 函数的基本性质 A卷(已下线)【导学案】《第三章 函数概念与性质》本章小结-2021-2022学年高一数学《新教材同步精典导学案》(人教A版2019必修第一册)
名校
解题方法
4 . 关于函数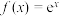 ,
,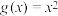 ,下列说法正确的是( )
,下列说法正确的是( )
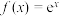 ,
,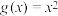 ,下列说法正确的是( )
,下列说法正确的是( )A.若过点 可以作曲线 可以作曲线 的两条切线,则 的两条切线,则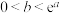 |
B.若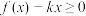 在 在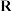 上恒成立,则实数 上恒成立,则实数 的取值范围为 的取值范围为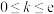 |
C.若 在 在 上恒成立,则 上恒成立,则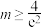 |
D.若函数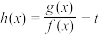 有且只有一个零点,则实数 有且只有一个零点,则实数 的范围为 的范围为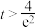 |
您最近一年使用:0次
2024-02-27更新
|
1109次组卷
|
4卷引用:重庆市璧山中学校2023-2024学年高二下学期第一次月考数学试题
名校
5 . 圆形是古代人最早从太阳、阴历十五的月亮得到圆的概念的.一直到两千多年前我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也.意思是说:圆有一个圆心,圆心到圆周的长都相等.现在以点 为圆心,2为半径的圆上取任意一点
为圆心,2为半径的圆上取任意一点 ,若
,若 的取值与x、y无关,则实数a的取值范围是
的取值与x、y无关,则实数a的取值范围是____________ .
 为圆心,2为半径的圆上取任意一点
为圆心,2为半径的圆上取任意一点 ,若
,若 的取值与x、y无关,则实数a的取值范围是
的取值与x、y无关,则实数a的取值范围是
您最近一年使用:0次
2023-10-14更新
|
633次组卷
|
4卷引用:重庆市云阳县云阳高级中学校2023-2024学年高二上学期第二次月考数学试题
名校
6 . 若对圆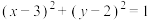 上任意一点
上任意一点 ,
, 的取值与
的取值与 无关,则实数a的取值范围是
无关,则实数a的取值范围是______ .
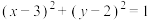 上任意一点
上任意一点 ,
, 的取值与
的取值与 无关,则实数a的取值范围是
无关,则实数a的取值范围是
您最近一年使用:0次
2023-12-08更新
|
394次组卷
|
13卷引用:重庆市第一中学2021-2022学年高二上学期11月月考数学试题
重庆市第一中学2021-2022学年高二上学期11月月考数学试题江西省南城第二中学2021-2022学年高二上学期第一次月考数学 试题上海市松江二中2023届高三上学期9月月考数学试题上海市华东师范大学附属东昌中学2023-2024学年高二上学期10月月考数学试题上海市东昌中学2023-2024学年高二上学期10月月考数学试题上海市黄浦区上海外国语大学附属大境中学2023-2024学年高二下学期3月月考数学试卷上海市崇明中学2021-2022学年高二下学期期中数学试题上海市嘉定区第二中学2022-2023学年高二上学期期中数学试题(已下线)专题03 圆的取值范围与最值问题题型全归纳 (2)(已下线)高二下期中真题精选(压轴40题专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)高二上学期期中【压轴60题考点专练】(选修一全部内容)-2022-2023学年高二数学考试满分全攻略(人教A版2019选修第一册)(已下线)2024届数学新高考Ⅰ卷精准模拟(八)(已下线)2.1.3 直线与圆的位置关系(八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
名校
7 . 设向量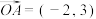 ,
,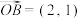 ,
, .
.
(1)若A、B、C三点共线,求实数x的取值;
(2)若 ,
, 的夹角为锐角,求实数x的取值范围.
的夹角为锐角,求实数x的取值范围.
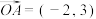 ,
,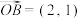 ,
, .
.(1)若A、B、C三点共线,求实数x的取值;
(2)若
 ,
, 的夹角为锐角,求实数x的取值范围.
的夹角为锐角,求实数x的取值范围.
您最近一年使用:0次
8 . 若函数 有3个不同的零点,分别记为
有3个不同的零点,分别记为 ,则下列说法正确的是( ).
,则下列说法正确的是( ).
 有3个不同的零点,分别记为
有3个不同的零点,分别记为 ,则下列说法正确的是( ).
,则下列说法正确的是( ).A. 是函数 是函数 的一个零点 的一个零点 |
B.a的取值范围是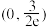 |
C. |
D.若 ,则a的范围是 ,则a的范围是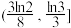 .(其中 .(其中 表示不超过实数x的最大整数,例如: 表示不超过实数x的最大整数,例如: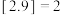 , , ) ) |
您最近一年使用:0次
名校
9 . 已知函数 .
.
(1)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的范围;
的范围;
(2)若实数 ,求
,求 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点 且
且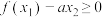 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的范围;
的范围;(2)若实数
 ,求
,求 的单调递增区间;
的单调递增区间;(3)若函数
 有两个极值点
有两个极值点 且
且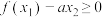 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-04-17更新
|
481次组卷
|
2卷引用:重庆第十一中学校2023-2024学年高二下学期3月月考数学试题
10 . 已知双曲线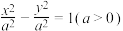 的右焦点为
的右焦点为 ,过右焦点
,过右焦点 作斜率为正的直线
作斜率为正的直线 ,直线
,直线 交双曲线的右支于
交双曲线的右支于 ,
, 两点,分别交两条渐近线于
两点,分别交两条渐近线于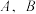 两点,点
两点,点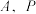 在第一象限,
在第一象限, 为原点.
为原点.
(1)求直线 斜率的取值范围;
斜率的取值范围;
(2)设 ,
, ,
, 的面积分别是
的面积分别是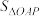 ,
,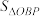 ,
,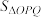 ,求
,求 的范围.
的范围.
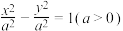 的右焦点为
的右焦点为 ,过右焦点
,过右焦点 作斜率为正的直线
作斜率为正的直线 ,直线
,直线 交双曲线的右支于
交双曲线的右支于 ,
, 两点,分别交两条渐近线于
两点,分别交两条渐近线于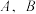 两点,点
两点,点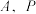 在第一象限,
在第一象限, 为原点.
为原点.(1)求直线
 斜率的取值范围;
斜率的取值范围;(2)设
 ,
, ,
, 的面积分别是
的面积分别是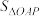 ,
,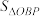 ,
,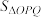 ,求
,求 的范围.
的范围.
您最近一年使用:0次
2022-10-16更新
|
954次组卷
|
6卷引用:重庆市南开中学2023届高三上学期第二次质量检测数学试题



