名校
解题方法
1 . 对于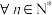 ,若数列
,若数列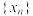 满足
满足 ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(1)已知数列1,2m,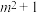 是“K数列”,求实数m的取值范围.
是“K数列”,求实数m的取值范围.
(2)是否存在首项为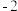 的等差数列
的等差数列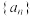 为“K数列”,且其前n项和
为“K数列”,且其前n项和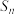 使得
使得 恒成立?若存在,求出数列
恒成立?若存在,求出数列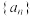 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3)已知各项均为正整数的等比数列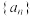 是“K数列”,数列
是“K数列”,数列 不是“K数列”,若
不是“K数列”,若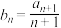 ,试判断数列
,试判断数列 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
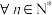 ,若数列
,若数列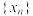 满足
满足 ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.(1)已知数列1,2m,
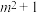 是“K数列”,求实数m的取值范围.
是“K数列”,求实数m的取值范围.(2)是否存在首项为
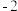 的等差数列
的等差数列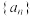 为“K数列”,且其前n项和
为“K数列”,且其前n项和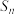 使得
使得 恒成立?若存在,求出数列
恒成立?若存在,求出数列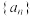 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.(3)已知各项均为正整数的等比数列
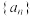 是“K数列”,数列
是“K数列”,数列 不是“K数列”,若
不是“K数列”,若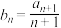 ,试判断数列
,试判断数列 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
您最近一年使用:0次
2024-09-07更新
|
1122次组卷
|
7卷引用:贵州省黔南州2023-2024学年高二下学期期末质量监测数学试卷
2 . 经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)之间的关系近似于线性相关关系.对某小组学生每周用于数学的学习时间 与数学成绩
与数学成绩 进行数据收集如表:
进行数据收集如表:
若由表中样本数据求得线性回归方程为 ,则实数
,则实数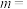
______ .
 与数学成绩
与数学成绩 进行数据收集如表:
进行数据收集如表: | 15 | 16 | 18 | 19 | 22 |
 | 102 | 98 | 115 |  | 120 |
 ,则实数
,则实数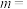
您最近一年使用:0次
名校
3 . 已知复数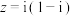 ,则
,则 ( )
( )
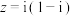 ,则
,则 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
2024-08-17更新
|
766次组卷
|
10卷引用:贵州省贵阳市南明区部分学校2023-2024学年高一下学期6月联考数学试题
(已下线)贵州省贵阳市南明区部分学校2023-2024学年高一下学期6月联考数学试题吉林省长春市汽车经济技术开发区第三中学2023-2024学年高二下学期7月期末考试数学试题浙江省宁波市五校联盟2023-2024学年高一下学期4月期中联考数学试题(已下线)5.2.2复数的乘法与除法-【帮课堂】(北师大版2019必修第二册)(已下线)2024年新课标全国Ⅱ卷数学真题平行卷(提升)浙江省金华市曙光学校2023-2024学年高一下学期5月期中考试数学试题广西南宁市第二中学2024-2025学年高三上学期8月开学考试数学试题广西南宁市第三中学2025届高三上学期9月适应性测试数学试题新疆维吾尔自治区和田地区墨玉县第一中学2025届高三上学期9月月考测试数学试题江西省赣州市于都县第二中学2025届高三上学期第一次月考试数学试题
名校
解题方法
4 . 已知向量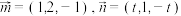 ,且
,且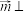 平面
平面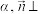 平面
平面 ,若平面
,若平面 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为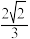 ,则实数
,则实数 的值为( )
的值为( )
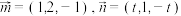 ,且
,且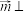 平面
平面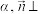 平面
平面 ,若平面
,若平面 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为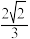 ,则实数
,则实数 的值为( )
的值为( )A. 或 或 | B. 或1 或1 | C. 或2 或2 | D. |
您最近一年使用:0次
2024-07-26更新
|
828次组卷
|
21卷引用:贵州省六盘水市盘州市第一中学2023-2024学年高二上学期期末考试数学试题
贵州省六盘水市盘州市第一中学2023-2024学年高二上学期期末考试数学试题云南省曲靖市沾益区第一中学2023-2024学年高二上学期期末考试数学试题河北省石家庄市河北赵县中学、高邑县第一中学2023-2024学年高二下学期5月质量检测数学试题(已下线)第06讲 用空间向量研究距离、夹角问题-【暑假自学课】(人教A版2019选择性必修第一册)(已下线)第04讲 直线与平面的夹角、二面角-【暑假自学课】(人教B版2019选择性必修第一册)新疆库车市第一中学2023-2024学年高二上学期期末考试数学试题云南省昆明市东川区第一中学2023-2024学年高二下学期第六次月考数学试题甘肃省定西临洮县文峰中学2023-2024学年高二下学期第二次月考数学试题(已下线)1.2.4 二面角——课堂例题福建省部分优质高中2024~2025学年高二上学期入学质量检测数学试卷(已下线)1.2.4 二面角——课堂例题云南省文山州西畴县第二中学2024-2025学年高二上学期9月月考数学试题河南省平顶山市叶县高级中学2024-2025学年高二上学期9月月考数学试卷广东省广州市番禺中学2024-2025学年高二上学期9月月考数学试卷广东省深圳市龙岗区广东实验中学深圳学校2024-2025学年高二上学期10月月考数学试题山西省大同市阳高县第四中学2024-2025学年高二上学期9月月考数学试题河北省石家庄市精英中学2023-2024学年高二上学期第一次调研考试数学试题吉林省桦甸市第一中学2024届高三上学期基础知识检测数学试题广西壮族自治区崇左市大新县民族高级中学2023-2024学年高二上学期期中考试数学试题内蒙古鄂尔多斯市第二中学2023-2024学年高二上学期12月月考数学试题新疆昌吉回族自治州阜康市第一中学2023-2024学年高二上学期第二次月考数学试题
5 . 如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, 平面
平面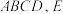 为
为 的中点.
的中点. 与直线
与直线 相交于点
相交于点 ,求证:
,求证:
 平面
平面 ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的大小.
所成角的大小.
 中,底面
中,底面 为菱形,
为菱形, 平面
平面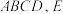 为
为 的中点.
的中点.
 与直线
与直线 相交于点
相交于点 ,求证:
,求证:
 平面
平面 ;
;(2)若
 ,求直线
,求直线 与平面
与平面 所成角的大小.
所成角的大小.
您最近一年使用:0次
解题方法
6 . 在 中,
中, 是
是 边上靠近点
边上靠近点 的三等分点,
的三等分点, 是
是 的中点,若
的中点,若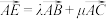 ,则
,则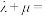 ( )
( )
 中,
中, 是
是 边上靠近点
边上靠近点 的三等分点,
的三等分点, 是
是 的中点,若
的中点,若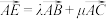 ,则
,则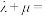 ( )
( )| A.0 | B.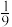 | C. | D.1 |
您最近一年使用:0次
解题方法
7 . 如图,从一个半径为 的圆形纸板中剪出一块最大的正三角形纸板,并将此正三角形纸板折叠成一个正四面体,则该正四面体外接球的表面积为( )
的圆形纸板中剪出一块最大的正三角形纸板,并将此正三角形纸板折叠成一个正四面体,则该正四面体外接球的表面积为( )
 的圆形纸板中剪出一块最大的正三角形纸板,并将此正三角形纸板折叠成一个正四面体,则该正四面体外接球的表面积为( )
的圆形纸板中剪出一块最大的正三角形纸板,并将此正三角形纸板折叠成一个正四面体,则该正四面体外接球的表面积为( )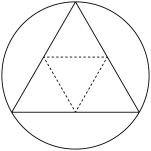
A. | B. |
C.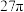 | D.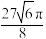 |
您最近一年使用:0次
8 . 定义:若椭圆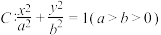 上的两个点
上的两个点 满足
满足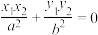 ,则称
,则称 为该椭圆的一个“共轭点对”.
为该椭圆的一个“共轭点对”.
如图, 为椭圆
为椭圆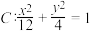 的“共轭点对”,已知
的“共轭点对”,已知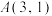 ,且点
,且点 在直线
在直线 上,直线
上,直线 过原点.
过原点.

(1)求直线 的方程;
的方程;
(2)已知 是椭圆
是椭圆 上的两点,
上的两点, 为坐标原点,且
为坐标原点,且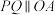 .
.
(i)求证:线段 被直线
被直线 平分;
平分;
(ii)若点 在第二象限,直线
在第二象限,直线 与
与 相交于点
相交于点 ,点
,点 为
为 的中点,求
的中点,求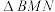 面积的最大值.
面积的最大值.
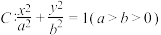 上的两个点
上的两个点 满足
满足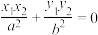 ,则称
,则称 为该椭圆的一个“共轭点对”.
为该椭圆的一个“共轭点对”.如图,
 为椭圆
为椭圆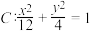 的“共轭点对”,已知
的“共轭点对”,已知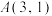 ,且点
,且点 在直线
在直线 上,直线
上,直线 过原点.
过原点.
(1)求直线
 的方程;
的方程;(2)已知
 是椭圆
是椭圆 上的两点,
上的两点, 为坐标原点,且
为坐标原点,且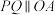 .
.(i)求证:线段
 被直线
被直线 平分;
平分;(ii)若点
 在第二象限,直线
在第二象限,直线 与
与 相交于点
相交于点 ,点
,点 为
为 的中点,求
的中点,求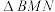 面积的最大值.
面积的最大值.
您最近一年使用:0次
解题方法
9 . 圆锥曲线具有丰富的光学性质.双曲线的光学性质:从双曲线的一个焦点 处发出的光线,经过双曲线在点
处发出的光线,经过双曲线在点 处反射后,反射光线所在直线经过另一个焦点
处反射后,反射光线所在直线经过另一个焦点 ,且双曲线在点
,且双曲线在点 处的切线平分
处的切线平分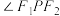 .如图,对称轴都在坐标轴上的等轴双曲线
.如图,对称轴都在坐标轴上的等轴双曲线 过点
过点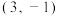 ,其左、右焦点分别为
,其左、右焦点分别为 .若从
.若从 发出的光线经双曲线右支上一点
发出的光线经双曲线右支上一点 反射的光线为
反射的光线为 ,点
,点 处的切线交
处的切线交 轴于点
轴于点 ,则下列说法正确的是( )
,则下列说法正确的是( )
 处发出的光线,经过双曲线在点
处发出的光线,经过双曲线在点 处反射后,反射光线所在直线经过另一个焦点
处反射后,反射光线所在直线经过另一个焦点 ,且双曲线在点
,且双曲线在点 处的切线平分
处的切线平分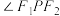 .如图,对称轴都在坐标轴上的等轴双曲线
.如图,对称轴都在坐标轴上的等轴双曲线 过点
过点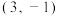 ,其左、右焦点分别为
,其左、右焦点分别为 .若从
.若从 发出的光线经双曲线右支上一点
发出的光线经双曲线右支上一点 反射的光线为
反射的光线为 ,点
,点 处的切线交
处的切线交 轴于点
轴于点 ,则下列说法正确的是( )
,则下列说法正确的是( )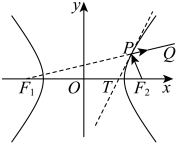
A.双曲线 的方程为 的方程为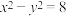 |
B.过点 且垂直于 且垂直于 的直线平分 的直线平分 |
C.若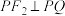 ,则 ,则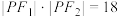 |
D.若 ,则 ,则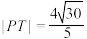 |
您最近一年使用:0次
解题方法
10 . 如图1,已知直角梯形AEFD中, ,点B,C分别在AE,DF上,且
,点B,C分别在AE,DF上,且 ,
, ,
, ,
,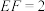 ,将图1沿BC翻折,使平面
,将图1沿BC翻折,使平面 平面BEFC得图2.
平面BEFC得图2.
(2)当 时,求平面AEF与平面CEF的夹角的正切值.
时,求平面AEF与平面CEF的夹角的正切值.
 ,点B,C分别在AE,DF上,且
,点B,C分别在AE,DF上,且 ,
, ,
, ,
,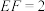 ,将图1沿BC翻折,使平面
,将图1沿BC翻折,使平面 平面BEFC得图2.
平面BEFC得图2.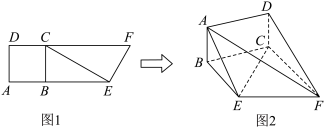
(2)当
 时,求平面AEF与平面CEF的夹角的正切值.
时,求平面AEF与平面CEF的夹角的正切值.
您最近一年使用:0次
2024-07-18更新
|
379次组卷
|
3卷引用:贵州省毕节市2023-2024学年高二下学期期末联考数学试题
贵州省毕节市2023-2024学年高二下学期期末联考数学试题单元测试B卷——第一章 空间向量与立体几何(已下线)压轴题06 空间向量与立体几何4大类型专练-【常考压轴题】(人教B版2019选择性必修第一册)



