名校
解题方法
1 . 已知二次函数 的图象过
的图象过 ,且函数图象顶点的横坐标为
,且函数图象顶点的横坐标为 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 在区间
在区间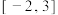 上的值域.
上的值域.
 的图象过
的图象过 ,且函数图象顶点的横坐标为
,且函数图象顶点的横坐标为 .
.(1)求函数
 的解析式;
的解析式;(2)求函数
 在区间
在区间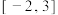 上的值域.
上的值域.
您最近一年使用:0次
名校
2 . 若函数Q在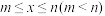 上的最大值记为
上的最大值记为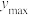 ,最小值记为
,最小值记为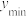 ,且满足
,且满足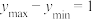 ,则称函数Q是在
,则称函数Q是在 上的“平稳函数”.
上的“平稳函数”.
(1)函数① ;②
;②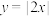 ;③
;③ ,其中函数______是在
,其中函数______是在 上的“平稳函数”(填序号);
上的“平稳函数”(填序号);
(2)已知函数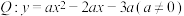 .
.
①当 时,函数Q是在
时,函数Q是在 上的“平稳函数”,求
上的“平稳函数”,求 的值;
的值;
②已知函数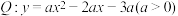 ,若函数Q是在
,若函数Q是在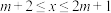 (
( 为整数)上的“平稳函数”,且存在整数
为整数)上的“平稳函数”,且存在整数 ,使得
,使得 ,求
,求 的值.
的值.
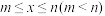 上的最大值记为
上的最大值记为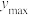 ,最小值记为
,最小值记为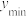 ,且满足
,且满足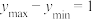 ,则称函数Q是在
,则称函数Q是在 上的“平稳函数”.
上的“平稳函数”.(1)函数①
 ;②
;②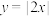 ;③
;③ ,其中函数______是在
,其中函数______是在 上的“平稳函数”(填序号);
上的“平稳函数”(填序号);(2)已知函数
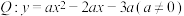 .
.①当
 时,函数Q是在
时,函数Q是在 上的“平稳函数”,求
上的“平稳函数”,求 的值;
的值;②已知函数
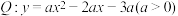 ,若函数Q是在
,若函数Q是在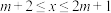 (
( 为整数)上的“平稳函数”,且存在整数
为整数)上的“平稳函数”,且存在整数 ,使得
,使得 ,求
,求 的值.
的值.
您最近一年使用:0次
7日内更新
|
98次组卷
|
2卷引用:重庆市第十一中学校教育集团2024-2025学年高一上学期期中考试数学试题
名校
3 . 我们知道,函数 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数.可以将其推广为:函数
为奇函数.可以将其推广为:函数 的图象关于点
的图象关于点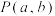 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数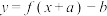 是奇函数.已知函数
是奇函数.已知函数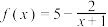 .
.
(1)求函数 图象的对称中心;
图象的对称中心;
(2)已知函数 关于点
关于点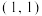 对称,且当
对称,且当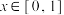 时,
时,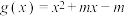 .若对任意
.若对任意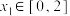 ,总存在
,总存在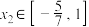 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数.可以将其推广为:函数
为奇函数.可以将其推广为:函数 的图象关于点
的图象关于点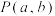 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数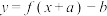 是奇函数.已知函数
是奇函数.已知函数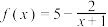 .
.(1)求函数
 图象的对称中心;
图象的对称中心;(2)已知函数
 关于点
关于点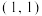 对称,且当
对称,且当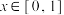 时,
时,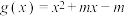 .若对任意
.若对任意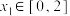 ,总存在
,总存在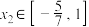 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 已知 ,
,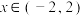 .
.
(1)求证:函数 在区间
在区间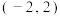 上是增函数;
上是增函数;
(2)求函数 在区间
在区间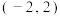 上的值域.
上的值域.
 ,
,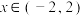 .
.(1)求证:函数
 在区间
在区间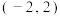 上是增函数;
上是增函数;(2)求函数
 在区间
在区间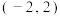 上的值域.
上的值域.
您最近一年使用:0次
7日内更新
|
1276次组卷
|
2卷引用:重庆市长寿中学校2024-2025学年高一上学期11月期中测试数学试题
名校
5 . 某学校有一四边形地块,为了提高校园土地的利用率,现把其中的一部分作为学校生物综合实践基地.如图所示,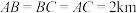 ,
, 是
是 中点,
中点, 分别在
分别在 、
、 上,
上, 拟作为花草种植区,四边形
拟作为花草种植区,四边形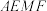 拟作为景观欣赏区,
拟作为景观欣赏区,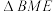 拟作为谷物蔬菜区,
拟作为谷物蔬菜区, 和
和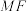 拟建造快速通道,
拟建造快速通道,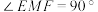 ,记
,记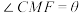 .(快速通道的宽度忽略不计)
.(快速通道的宽度忽略不计)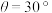 ,求景观欣赏区所在四边形
,求景观欣赏区所在四边形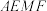 的面积;
的面积;
(2)当 取何值时,可使快速通道
取何值时,可使快速通道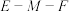 的路程最短?最短路程是多少?
的路程最短?最短路程是多少?
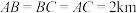 ,
, 是
是 中点,
中点, 分别在
分别在 、
、 上,
上, 拟作为花草种植区,四边形
拟作为花草种植区,四边形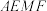 拟作为景观欣赏区,
拟作为景观欣赏区,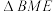 拟作为谷物蔬菜区,
拟作为谷物蔬菜区, 和
和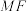 拟建造快速通道,
拟建造快速通道, ,记
,记 .(快速通道的宽度忽略不计)
.(快速通道的宽度忽略不计)
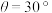 ,求景观欣赏区所在四边形
,求景观欣赏区所在四边形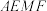 的面积;
的面积;(2)当
 取何值时,可使快速通道
取何值时,可使快速通道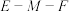 的路程最短?最短路程是多少?
的路程最短?最短路程是多少?
您最近一年使用:0次
6 . 已知函数 .
.
(1)若 有三个零点,求实数
有三个零点,求实数 的取值范围;
的取值范围;
(2)若函数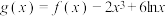 在
在 上的最小值为
上的最小值为 ,求
,求 在
在 上的最大值.
上的最大值.
 .
.(1)若
 有三个零点,求实数
有三个零点,求实数 的取值范围;
的取值范围;(2)若函数
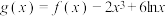 在
在 上的最小值为
上的最小值为 ,求
,求 在
在 上的最大值.
上的最大值.
您最近一年使用:0次
名校
7 . 已知函数 .
.
(1)判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)判断 在区间
在区间 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(3)求函数 在
在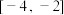 上的最大值和最小值.
上的最大值和最小值.
 .
.(1)判断
 的奇偶性,并说明理由;
的奇偶性,并说明理由;(2)判断
 在区间
在区间 上的单调性,并用定义证明;
上的单调性,并用定义证明;(3)求函数
 在
在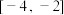 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2024-03-12更新
|
224次组卷
|
2卷引用:重庆市永川双石中学校2023-2024学年高一上学期半期考试(期中)数学试题
名校
8 . 函数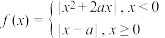 ,其中
,其中 为常数,
为常数,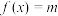 有
有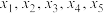 这5个不同的实数解,并且有
这5个不同的实数解,并且有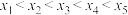 .
.
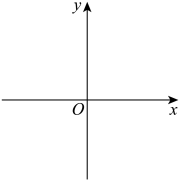
(1)在坐标系中画出函数 的图象,并求
的图象,并求 的取值范围(用
的取值范围(用 表示);
表示);
(2)若 ,求
,求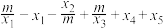 的最小值.
的最小值.
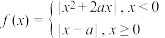 ,其中
,其中 为常数,
为常数,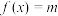 有
有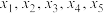 这5个不同的实数解,并且有
这5个不同的实数解,并且有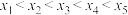 .
.
(1)在坐标系中画出函数
 的图象,并求
的图象,并求 的取值范围(用
的取值范围(用 表示);
表示);(2)若
 ,求
,求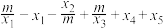 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
9 .  为定义在
为定义在 上的函数,且对任意实数
上的函数,且对任意实数 均满足
均满足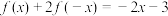 .
.
(1)求 的解析式;
的解析式;
(2)若存在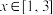 使得不等式
使得不等式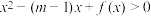 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 为定义在
为定义在 上的函数,且对任意实数
上的函数,且对任意实数 均满足
均满足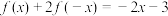 .
.(1)求
 的解析式;
的解析式;(2)若存在
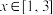 使得不等式
使得不等式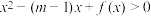 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-10更新
|
630次组卷
|
2卷引用:重庆市南开中学校2023-2024学年高一上学期期中数学试题
名校
解题方法
10 . 已知函数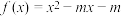 .
.
(1)若方程 恰有两个不同的正根,求实数
恰有两个不同的正根,求实数 的取值范围;
的取值范围;
(2)若
①求 在
在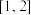 上的最大值
上的最大值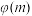 ;
;
②若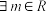 ,对
,对 有:
有: 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
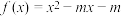 .
.(1)若方程
 恰有两个不同的正根,求实数
恰有两个不同的正根,求实数 的取值范围;
的取值范围;(2)若

①求
 在
在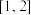 上的最大值
上的最大值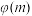 ;
;②若
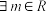 ,对
,对 有:
有: 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次



