1 . 已知幂函数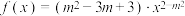 在
在 上单调递增.
上单调递增.
(1)求 的函数解析式;
的函数解析式;
(2)设 ,若
,若 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数 的取值范围;
的取值范围;
(3)若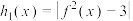 ,
,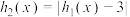 ,
,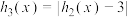 ,若
,若 ,求满足条件的
,求满足条件的 的取值范围.
的取值范围.
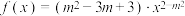 在
在 上单调递增.
上单调递增.(1)求
 的函数解析式;
的函数解析式;(2)设
 ,若
,若 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数 的取值范围;
的取值范围;(3)若
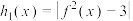 ,
,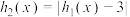 ,
,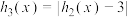 ,若
,若 ,求满足条件的
,求满足条件的 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-11更新
|
754次组卷
|
2卷引用:四川省成都市成都市第七中学2023-2024学年高一上学期期中数学试题
2 . 已知函数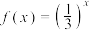 ,
, ,
, .则下列说法正确的是( )
.则下列说法正确的是( )
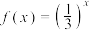 ,
, ,
, .则下列说法正确的是( )
.则下列说法正确的是( )A.函数 与函数 与函数 互为反函数 互为反函数 |
B.函数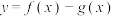 在区间 在区间 内没有零点 内没有零点 |
C.若a,b,c均为正实数,且满足 ,则 ,则 |
D.若函数 的图象与函数 的图象与函数 的图象和函数 的图象和函数 的图象在第一象限内交点的横坐标分别为 的图象在第一象限内交点的横坐标分别为 ,则 ,则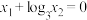 |
您最近一年使用:0次
2023-02-21更新
|
612次组卷
|
2卷引用:四川省成都市2022-2023学年高一上学期期末数学试题
名校
3 . 若在定义域内存在实数 ,使得
,使得 成立,则称函数有“飘移点”
成立,则称函数有“飘移点” .
.
(1)函数 是否有“飘移点”?请说明理由;
是否有“飘移点”?请说明理由;
(2)证明函数 在
在 上有“飘移点”;
上有“飘移点”;
(3)若函数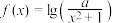 在
在 上有“飘移点”,求实数a的取值范围.
上有“飘移点”,求实数a的取值范围.
 ,使得
,使得 成立,则称函数有“飘移点”
成立,则称函数有“飘移点” .
.(1)函数
 是否有“飘移点”?请说明理由;
是否有“飘移点”?请说明理由;(2)证明函数
 在
在 上有“飘移点”;
上有“飘移点”;(3)若函数
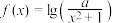 在
在 上有“飘移点”,求实数a的取值范围.
上有“飘移点”,求实数a的取值范围.
您最近一年使用:0次
2023-01-05更新
|
770次组卷
|
7卷引用:四川省宜宾市兴文第二中学校2023-2024学年高一下学期开学考试数学试题
名校
4 . 利普希兹条件是数学中一个关于函数光滑性的重要概念,设 定义在
定义在 上的函数,若对于
上的函数,若对于 中任意两点
中任意两点 ,都有
,都有 ,则称
,则称 是“
是“ -利普希兹条件函数”.
-利普希兹条件函数”.
(1)判断函数 ,
, 在
在 上是否为“1-利普希兹条件函数”;
上是否为“1-利普希兹条件函数”;
(2)若函数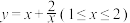 是“
是“ -利普希兹条件函数”,求
-利普希兹条件函数”,求 的最小值;
的最小值;
(3)设 ,若存在
,若存在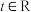 ,使
,使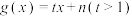 是“2024-利普希兹条件函数”,且关于
是“2024-利普希兹条件函数”,且关于 的方程
的方程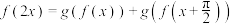 在
在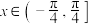 上有两个不相等实根,求
上有两个不相等实根,求 的取值范围.
的取值范围.
 定义在
定义在 上的函数,若对于
上的函数,若对于 中任意两点
中任意两点 ,都有
,都有 ,则称
,则称 是“
是“ -利普希兹条件函数”.
-利普希兹条件函数”.(1)判断函数
 ,
, 在
在 上是否为“1-利普希兹条件函数”;
上是否为“1-利普希兹条件函数”;(2)若函数
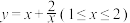 是“
是“ -利普希兹条件函数”,求
-利普希兹条件函数”,求 的最小值;
的最小值;(3)设
 ,若存在
,若存在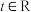 ,使
,使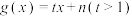 是“2024-利普希兹条件函数”,且关于
是“2024-利普希兹条件函数”,且关于 的方程
的方程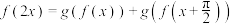 在
在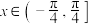 上有两个不相等实根,求
上有两个不相等实根,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-18更新
|
558次组卷
|
3卷引用:四川省成都市玉林中学2024-2025学年高三上学期10月诊断性评价数学试题
5 . 已知偶函数 满足
满足 ,且当
,且当 时,
时, .则下列说法正确的是( )
.则下列说法正确的是( )
 满足
满足 ,且当
,且当 时,
时, .则下列说法正确的是( )
.则下列说法正确的是( )A. 关于 关于 对称 对称 |
B.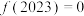 |
C.方程 ( ( 且 且 )在区间 )在区间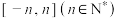 上恒有 上恒有 个不等的实数根 个不等的实数根 |
D.若方程 ( ( 且 且 )在区间 )在区间 有5个根,则 有5个根,则 的取值范围是 的取值范围是 |
您最近一年使用:0次
名校
解题方法
6 . 已知 为
为 上的偶函数,当
上的偶函数,当 时,
时,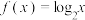 ,对于结论
,对于结论
(1)当 时,
时,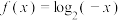 ;
;
(2)方程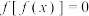 根的个数可以为
根的个数可以为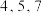 ;
;
(3)若函数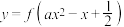 在区间
在区间 上恒为正,则实数
上恒为正,则实数 的范围是
的范围是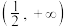 ;
;
(4)若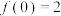 ,关于
,关于 的方程
的方程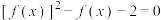 有
有 个不同的实根.
个不同的实根.
说法正确的序号是___ .
 为
为 上的偶函数,当
上的偶函数,当 时,
时,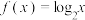 ,对于结论
,对于结论(1)当
 时,
时,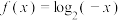 ;
;(2)方程
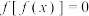 根的个数可以为
根的个数可以为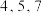 ;
;(3)若函数
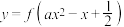 在区间
在区间 上恒为正,则实数
上恒为正,则实数 的范围是
的范围是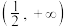 ;
;(4)若
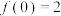 ,关于
,关于 的方程
的方程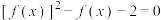 有
有 个不同的实根.
个不同的实根.说法正确的序号是
您最近一年使用:0次
名校
7 . 关于 的方程
的方程
(1)若方程无实根,求 的取值范围;
的取值范围;
(2)若方程有4个不等实根,求 的取值范围;
的取值范围;
(3)若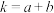 ,且满足
,且满足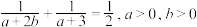 试判断方程根的个数.
试判断方程根的个数.
 的方程
的方程
(1)若方程无实根,求
 的取值范围;
的取值范围;(2)若方程有4个不等实根,求
 的取值范围;
的取值范围;(3)若
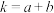 ,且满足
,且满足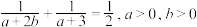 试判断方程根的个数.
试判断方程根的个数.
您最近一年使用:0次



