名校
解题方法
1 . 已知函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)若函数 在区间
在区间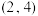 上不是单调函数,求
上不是单调函数,求 的取值范围;
的取值范围;
(3)若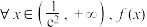 无零点,求
无零点,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;(2)若函数
 在区间
在区间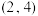 上不是单调函数,求
上不是单调函数,求 的取值范围;
的取值范围;(3)若
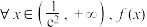 无零点,求
无零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-08-05更新
|
374次组卷
|
2卷引用:辽宁省七校协作体2024-2025学年高三上学期期初联考数学试题
解题方法
2 . 若方程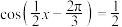 在区间
在区间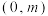 上有5个不相等的实数根,则
上有5个不相等的实数根,则 的取值范围为( )
的取值范围为( )
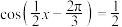 在区间
在区间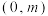 上有5个不相等的实数根,则
上有5个不相等的实数根,则 的取值范围为( )
的取值范围为( )A. | B.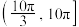 | C.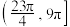 | D.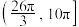 |
您最近一年使用:0次
名校
3 . 已知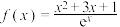 ,则( )
,则( )
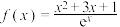 ,则( )
,则( )A.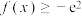 对 对 恒成立 恒成立 |
B.若函数 有两个不同的零点,则k的取值范围是 有两个不同的零点,则k的取值范围是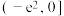 |
C.方程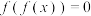 恰有3个实根 恰有3个实根 |
D.若关于x的不等式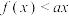 恰有1个负整数解,则a的取值范围为 恰有1个负整数解,则a的取值范围为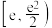 |
您最近一年使用:0次
2024-06-13更新
|
745次组卷
|
2卷引用:辽宁省沈阳市第二中学2025届高三上学期期初考试数学试卷
2024·全国·模拟预测
4 . 已知关于 的方程
的方程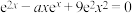 有4个不同的实数根,分别记为
有4个不同的实数根,分别记为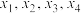 ,则
,则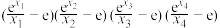 的取值范围为( )
的取值范围为( )
 的方程
的方程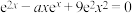 有4个不同的实数根,分别记为
有4个不同的实数根,分别记为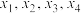 ,则
,则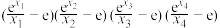 的取值范围为( )
的取值范围为( )A.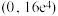 | B.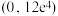 | C. | D.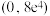 |
您最近一年使用:0次
2024-06-11更新
|
893次组卷
|
5卷引用:辽宁省沈阳市第二中学2025届高三上学期期初考试数学试卷
辽宁省沈阳市第二中学2025届高三上学期期初考试数学试卷(已下线)2024年普通高等学校招生全国统一考试数学文科猜题卷(六)(已下线)2024年普通高等学校招生全国统一考试数学理科猜题卷(六)(已下线)数学(全国卷理科03)四川省峨眉市第二中学校2024届高三适应性考试暨押题数学(理)试题
名校
解题方法
5 . 已知函数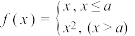 ,若存在实数
,若存在实数 ,使函数
,使函数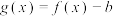 有两个零点,则
有两个零点,则 的取值范围是( )
的取值范围是( )
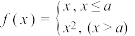 ,若存在实数
,若存在实数 ,使函数
,使函数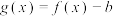 有两个零点,则
有两个零点,则 的取值范围是( )
的取值范围是( )A. | B. 且 且 | C. | D. 且 且 |
您最近一年使用:0次
2024-05-26更新
|
837次组卷
|
2卷引用:辽宁省沈阳市东北育才学校2024-2025学年高三上学期第一次模拟考试暨假期质量测试数学试卷
解题方法
6 . 已知函数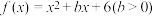 有唯一零点,函数
有唯一零点,函数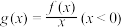 .
.
(1)求 的单调递增区间,并用定义法证明;
的单调递增区间,并用定义法证明;
(2)求 的值域.
的值域.
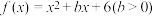 有唯一零点,函数
有唯一零点,函数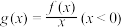 .
.(1)求
 的单调递增区间,并用定义法证明;
的单调递增区间,并用定义法证明;(2)求
 的值域.
的值域.
您最近一年使用:0次
名校
7 . 已知函数 ,
,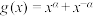
(1)直接写出
 时,
时, 的最小值.
的最小值.(2)
 时,
时,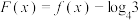 在
在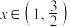 是否存在零点?给出结论并证明.
是否存在零点?给出结论并证明.(3)若
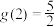 ,
,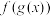 存在两个零点,求
存在两个零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-14更新
|
935次组卷
|
4卷引用:辽宁省葫芦岛市绥中县第一高级中学2023-2024学年高一下学期期初考试数学试题
辽宁省葫芦岛市绥中县第一高级中学2023-2024学年高一下学期期初考试数学试题辽宁省大连市2022-2023学年高一上学期期末数学模拟试题(已下线)高一上学期期末考试解答题压轴题50题专练-举一反三系列(已下线)专题2.3 幂函数与指、对数函数【九大题型】
8 . 已知函数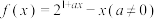 .
.
(1)若 ,求
,求 在
在 上的值域;
上的值域;
(2)若函数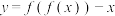 恰有两个零点,求
恰有两个零点,求 的取值范围.
的取值范围.
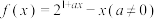 .
.(1)若
 ,求
,求 在
在 上的值域;
上的值域;(2)若函数
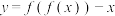 恰有两个零点,求
恰有两个零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-06更新
|
687次组卷
|
8卷引用:辽宁省朝阳市名校联考2023-2024学年高三上学期开学数学试题
辽宁省朝阳市名校联考2023-2024学年高三上学期开学数学试题辽宁省部分学校2023-2024学年高三上学期10月月考数学试题广东省湛江市部分学校2024届高三上学期十月考试数学试题山东省部分学校2023年高三上学期10月月考数学试题山西省晋中市平遥县第二中学校2024届高三上学期10月质检数学试题河南省商丘市虞城县2023-2024学年高三上学期11月月考数学试题(已下线)第09讲 第五章 一元函数的导数及其应用 重点题型章末总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第二册)(已下线)热点2-3 函数的图象及零点问题(8题型+满分技巧+限时检测)
9 . 已知函数 ,甲、乙、丙、丁四名同学研究
,甲、乙、丙、丁四名同学研究 在
在 上的零点分布情况,各得出一个结论:
上的零点分布情况,各得出一个结论:
甲:若 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为 ;
;
乙:若 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为 ;
;
丙:若 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为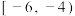 ;
;
丁:若 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为 .
.
则这四名同学中得出正确结论的是( )
 ,甲、乙、丙、丁四名同学研究
,甲、乙、丙、丁四名同学研究 在
在 上的零点分布情况,各得出一个结论:
上的零点分布情况,各得出一个结论:甲:若
 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为 ;
;乙:若
 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为 ;
;丙:若
 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为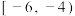 ;
;丁:若
 在
在 上有
上有 个零点,则实数
个零点,则实数 的取值范围为
的取值范围为 .
.则这四名同学中得出正确结论的是( )
| A.甲、丙、丁 | B.甲、乙 | C.乙、丙 | D.丙、丁 |
您最近一年使用:0次
名校
解题方法
10 . 已知偶函数 的定义域为
的定义域为 ,函数
,函数 ,且
,且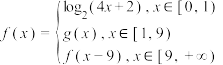 ,若
,若 在
在 上的图象与直线
上的图象与直线 恰有
恰有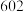 个公共点,则
个公共点,则 的取值范围为
的取值范围为__________ .
 的定义域为
的定义域为 ,函数
,函数 ,且
,且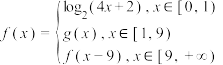 ,若
,若 在
在 上的图象与直线
上的图象与直线 恰有
恰有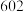 个公共点,则
个公共点,则 的取值范围为
的取值范围为
您最近一年使用:0次
2023-06-09更新
|
441次组卷
|
4卷引用:辽宁省沈阳市新民市高级中学2023-2024学年高三上学期9月份开学考试数学试题



