名校
1 . 已知定义在 上的函数
上的函数 的表达式为
的表达式为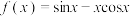 ,其所有的零点按从小到大的顺序组成数列
,其所有的零点按从小到大的顺序组成数列 (
(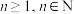 ).
).
(1)求函数 在区间
在区间 上的值域;
上的值域;
(2)求证:函数 在区间
在区间 (
(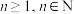 )上有且仅有一个零点;
)上有且仅有一个零点;
(3)求证: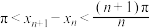 .
.
 上的函数
上的函数 的表达式为
的表达式为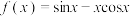 ,其所有的零点按从小到大的顺序组成数列
,其所有的零点按从小到大的顺序组成数列 (
(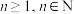 ).
).(1)求函数
 在区间
在区间 上的值域;
上的值域;(2)求证:函数
 在区间
在区间 (
(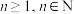 )上有且仅有一个零点;
)上有且仅有一个零点;(3)求证:
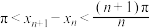 .
.
您最近一年使用:0次
2024-04-19更新
|
1195次组卷
|
4卷引用:广东省肇庆市德庆县香山中学2024-2025学年高三上学期8月月考数学试题
广东省肇庆市德庆县香山中学2024-2025学年高三上学期8月月考数学试题上海市闵行区2024届高三下学期学业质量调研(二模)数学试卷(已下线)压轴题01集合新定义、函数与导数13题型汇总 -1(已下线)专题4 导数中的隐零点问题【练】
名校
解题方法
2 . 设函数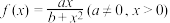 ,满足:①
,满足:① ;②对任意
;②对任意 ,
,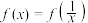 恒成立.
恒成立. 的解析式.
的解析式.
(2)设矩形 的一边
的一边 在
在 轴上,顶点
轴上,顶点 ,
, 在函数
在函数 的图象上.设矩形
的图象上.设矩形 的面积为
的面积为 ,求证:
,求证: .
.
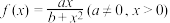 ,满足:①
,满足:① ;②对任意
;②对任意 ,
,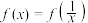 恒成立.
恒成立.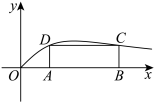
 的解析式.
的解析式.(2)设矩形
 的一边
的一边 在
在 轴上,顶点
轴上,顶点 ,
, 在函数
在函数 的图象上.设矩形
的图象上.设矩形 的面积为
的面积为 ,求证:
,求证: .
.
您最近一年使用:0次
2023-11-09更新
|
609次组卷
|
6卷引用:广东省揭阳市两校2024-2025学年高三上学期8月联考数学试题
3 . 如果定义域为 的函数
的函数 同时满足以下三个条件:(1)对任意的
同时满足以下三个条件:(1)对任意的 ,总有
,总有 ;(2)
;(2) ;(3)当
;(3)当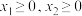 ,且
,且 时,
时,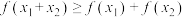 恒成立.则称
恒成立.则称 为“友谊函数”.请解答下列问题:
为“友谊函数”.请解答下列问题:
(1)已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)判断函数 是否为“友谊函数”?并说明理由;
是否为“友谊函数”?并说明理由;
(3)已知 为“友谊函数”,存在
为“友谊函数”,存在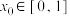 ,使得
,使得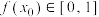 ,且
,且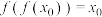 ,证明:
,证明: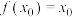 .
.
 的函数
的函数 同时满足以下三个条件:(1)对任意的
同时满足以下三个条件:(1)对任意的 ,总有
,总有 ;(2)
;(2) ;(3)当
;(3)当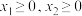 ,且
,且 时,
时,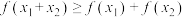 恒成立.则称
恒成立.则称 为“友谊函数”.请解答下列问题:
为“友谊函数”.请解答下列问题:(1)已知
 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;(2)判断函数
 是否为“友谊函数”?并说明理由;
是否为“友谊函数”?并说明理由;(3)已知
 为“友谊函数”,存在
为“友谊函数”,存在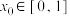 ,使得
,使得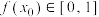 ,且
,且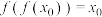 ,证明:
,证明: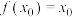 .
.
您最近一年使用:0次
4 . 设函数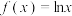 ,
, .
.
(1)当 时,比较
时,比较 和
和 的大小关系;
的大小关系;
(2)证明: 的图象与
的图象与 的图象关于直线
的图象关于直线 对称;
对称;
(3)在平面直角坐标系中,若以 为圆心的圆交
为圆心的圆交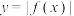 的图象于A,B两点,证明:
的图象于A,B两点,证明: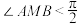 .
.
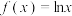 ,
, .
.(1)当
 时,比较
时,比较 和
和 的大小关系;
的大小关系;(2)证明:
 的图象与
的图象与 的图象关于直线
的图象关于直线 对称;
对称;(3)在平面直角坐标系中,若以
 为圆心的圆交
为圆心的圆交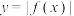 的图象于A,B两点,证明:
的图象于A,B两点,证明: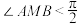 .
.
您最近一年使用:0次
名校
5 . 若对任意的实数k,b,函数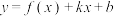 与直线
与直线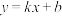 总相切,则称函数
总相切,则称函数 为“恒切函数”.
为“恒切函数”.
(1)判断函数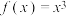 是否为“恒切函数”;
是否为“恒切函数”;
(2)若函数 是“恒切函数”,求证:
是“恒切函数”,求证: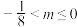 .
.
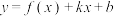 与直线
与直线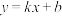 总相切,则称函数
总相切,则称函数 为“恒切函数”.
为“恒切函数”.(1)判断函数
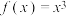 是否为“恒切函数”;
是否为“恒切函数”;(2)若函数
 是“恒切函数”,求证:
是“恒切函数”,求证: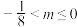 .
.
您最近一年使用:0次
2023-04-25更新
|
622次组卷
|
3卷引用:广东省茂名市华南师范大学附属电白学校2023届高三下学期5月调研数学试题
名校
6 . 对于函数 ,把
,把 称为函数
称为函数 的一阶导,令
的一阶导,令 ,则将
,则将 称为函数
称为函数 的二阶导,以此类推
的二阶导,以此类推 得到n阶导.为了方便书写,我们将n阶导用
得到n阶导.为了方便书写,我们将n阶导用 表示.
表示.
(1)已知函数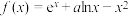 ,写出其二阶导函数并讨论其二阶导函数单调性.
,写出其二阶导函数并讨论其二阶导函数单调性.
(2)现定义一个新的数列:在 取
取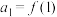 作为数列的首项,并将
作为数列的首项,并将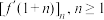 作为数列的第
作为数列的第 项.我们称该数列为
项.我们称该数列为 的“n阶导数列”
的“n阶导数列”
①若函数 (
( ),数列
),数列 是
是 的“n阶导数列”,取Tn为
的“n阶导数列”,取Tn为 的前n项积,求数列
的前n项积,求数列 的通项公式.
的通项公式.
②在我们高中阶段学过的初等函数中,是否有函数使得该函数的“n阶导数列”为严格减数列且为无穷数列,请写出它并证明此结论.(写出一个即可)
 ,把
,把 称为函数
称为函数 的一阶导,令
的一阶导,令 ,则将
,则将 称为函数
称为函数 的二阶导,以此类推
的二阶导,以此类推 得到n阶导.为了方便书写,我们将n阶导用
得到n阶导.为了方便书写,我们将n阶导用 表示.
表示.(1)已知函数
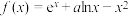 ,写出其二阶导函数并讨论其二阶导函数单调性.
,写出其二阶导函数并讨论其二阶导函数单调性.(2)现定义一个新的数列:在
 取
取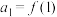 作为数列的首项,并将
作为数列的首项,并将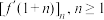 作为数列的第
作为数列的第 项.我们称该数列为
项.我们称该数列为 的“n阶导数列”
的“n阶导数列”①若函数
 (
( ),数列
),数列 是
是 的“n阶导数列”,取Tn为
的“n阶导数列”,取Tn为 的前n项积,求数列
的前n项积,求数列 的通项公式.
的通项公式.②在我们高中阶段学过的初等函数中,是否有函数使得该函数的“n阶导数列”为严格减数列且为无穷数列,请写出它并证明此结论.(写出一个即可)
您最近一年使用:0次
2023-12-16更新
|
975次组卷
|
7卷引用:广东番禺中学2023-2024学年高三第六次段考数学试题
广东番禺中学2023-2024学年高三第六次段考数学试题广东省广州市番禺中学2024届高三第六次段考数学试题上海市嘉定区2024届高三上学期质量调研数学试题上海市普陀区长征中学2024届高三上学期10月月考数学试题(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)信息必刷卷05(上海专用)(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)
名校
解题方法
7 . 拟合(Fittiong)和插值(Imorterpolation)都是利用已知的离散数据点来构造一个能够反映数据变化规律的近似函数,并以此预测或估计未知数据的方法.拟合方法在整体上寻求最好地逼近数据,适用于给定数据可能包含误差的情况,比如线性回归就是一种拟合方法;而插值方法要求近似函数经过所有的已知数据点.适用于需要高精度模型的场景,实际应用中常用多项式函数来逼近原函数,我们称之为移项式插值.例如,为了得到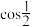 的近似值,我们对函数
的近似值,我们对函数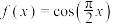 进行多项式插值.设一次函数
进行多项式插值.设一次函数 满足
满足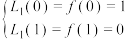 ,可得
,可得 在
在 上的一次插值多项式
上的一次插值多项式 ,由此可计算出
,由此可计算出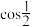 的“近似值”
的“近似值”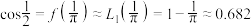 ,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数
,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数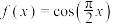 在
在 上的二次埃尔米特插值多项式
上的二次埃尔米特插值多项式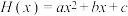 满足
满足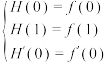
(1)求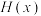 ,并证明当
,并证明当 时,
时, ;
;
(2)若当 时,
时,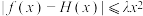 ,求实数
,求实数 的取值范围;
的取值范围;
(3)利用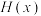 计算
计算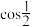 的近似值,并证明其误差不超过
的近似值,并证明其误差不超过 .
.
(参考数据: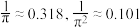 ;结果精确到0.001)
;结果精确到0.001)
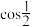 的近似值,我们对函数
的近似值,我们对函数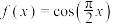 进行多项式插值.设一次函数
进行多项式插值.设一次函数 满足
满足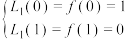 ,可得
,可得 在
在 上的一次插值多项式
上的一次插值多项式 ,由此可计算出
,由此可计算出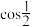 的“近似值”
的“近似值”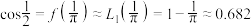 ,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数
,显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差,除了要求插值函数与原函数在给定节点处的函数值相等,还可要求在部分节点处的导数值也相等,甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特(Hermite)插值多项式.已知函数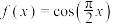 在
在 上的二次埃尔米特插值多项式
上的二次埃尔米特插值多项式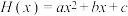 满足
满足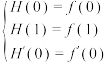
(1)求
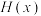 ,并证明当
,并证明当 时,
时, ;
;(2)若当
 时,
时,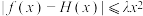 ,求实数
,求实数 的取值范围;
的取值范围;(3)利用
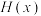 计算
计算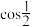 的近似值,并证明其误差不超过
的近似值,并证明其误差不超过 .
.(参考数据:
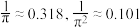 ;结果精确到0.001)
;结果精确到0.001)
您最近一年使用:0次
2024-07-11更新
|
371次组卷
|
2卷引用:广东省四校(华附、省实、广雅、深中)2023-2024学年高二下学期期末联考数学试题
2023·全国·模拟预测
8 . 一类项目若投资1元,投资成功的概率为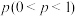 .如果投资成功,会获得
.如果投资成功,会获得 元的回报
元的回报 ;如果投资失败,则会亏掉1元本金.为了规避风险,分多次投资该类项目,设每次投资金额为剩余本金的
;如果投资失败,则会亏掉1元本金.为了规避风险,分多次投资该类项目,设每次投资金额为剩余本金的 ,1956年约翰·拉里·凯利计算得出,多次投资的平均回报率函数为
,1956年约翰·拉里·凯利计算得出,多次投资的平均回报率函数为 ,并提出了凯利公式.
,并提出了凯利公式.
(1)证明:当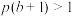 时,使得平均回报率
时,使得平均回报率 最高的投资比例
最高的投资比例 满足凯利公式
满足凯利公式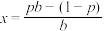 ;
;
(2)若 ,
, ,求函数
,求函数 在
在 上的零点个数.
上的零点个数.
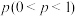 .如果投资成功,会获得
.如果投资成功,会获得 元的回报
元的回报 ;如果投资失败,则会亏掉1元本金.为了规避风险,分多次投资该类项目,设每次投资金额为剩余本金的
;如果投资失败,则会亏掉1元本金.为了规避风险,分多次投资该类项目,设每次投资金额为剩余本金的 ,1956年约翰·拉里·凯利计算得出,多次投资的平均回报率函数为
,1956年约翰·拉里·凯利计算得出,多次投资的平均回报率函数为 ,并提出了凯利公式.
,并提出了凯利公式.(1)证明:当
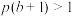 时,使得平均回报率
时,使得平均回报率 最高的投资比例
最高的投资比例 满足凯利公式
满足凯利公式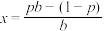 ;
;(2)若
 ,
, ,求函数
,求函数 在
在 上的零点个数.
上的零点个数.
您最近一年使用:0次
2024-01-17更新
|
922次组卷
|
5卷引用:广东省广州市广东实验中学2024届高三上学期大湾区数学冲刺卷(三)
名校
解题方法
9 . 设函数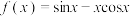 ,
, .
.
(1)①当 时,证明:
时,证明: ;
;
②当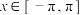 时,求
时,求 的值域;
的值域;
(2)若数列 满足
满足 ,
,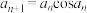 ,
, ,证明:
,证明: (
( ).
).
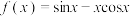 ,
, .
.(1)①当
 时,证明:
时,证明: ;
;②当
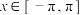 时,求
时,求 的值域;
的值域;(2)若数列
 满足
满足 ,
,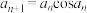 ,
, ,证明:
,证明: (
( ).
).
您最近一年使用:0次
2023-12-30更新
|
1304次组卷
|
5卷引用:广东省广州市华南师大附中2024届高三上学期大湾区数学预测卷(一)
广东省广州市华南师大附中2024届高三上学期大湾区数学预测卷(一)重庆市育才中学、万州高级中学及西南大学附中2024届高三上学期12月三校联考数学试题(已下线)四川省成都市第七中学2024届高三上学期期末数学(理)试题(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编(已下线)重难点突破01 数列的综合应用(十三大题型)-2
10 . 已知函数 ,函数
,函数 是定义在
是定义在 的可导函数,其导数为
的可导函数,其导数为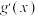 ,满足
,满足 .
.
(1)令函数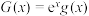 ,求证:
,求证: 在
在 上是减函数;
上是减函数;
(2)若 在
在 上单调递减,求实数
上单调递减,求实数 取值范围;
取值范围;
(3)对任意正数 ,试比较
,试比较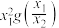 与
与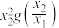 的大小.
的大小.
 ,函数
,函数 是定义在
是定义在 的可导函数,其导数为
的可导函数,其导数为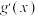 ,满足
,满足 .
.(1)令函数
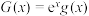 ,求证:
,求证: 在
在 上是减函数;
上是减函数;(2)若
 在
在 上单调递减,求实数
上单调递减,求实数 取值范围;
取值范围;(3)对任意正数
 ,试比较
,试比较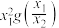 与
与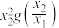 的大小.
的大小.
您最近一年使用:0次



