名校
1 . 已知 ,不等式
,不等式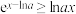 恒成立,则
恒成立,则 的最大值为( )
的最大值为( )
 ,不等式
,不等式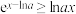 恒成立,则
恒成立,则 的最大值为( )
的最大值为( )A. | B.1 | C. | D.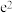 |
您最近一年使用:0次
名校
2 . 设函数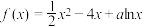 ,若函数
,若函数 存在两个极值点
存在两个极值点 ,且不等式
,且不等式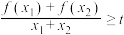 恒成立,则t的取值范围为( ).
恒成立,则t的取值范围为( ).
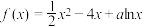 ,若函数
,若函数 存在两个极值点
存在两个极值点 ,且不等式
,且不等式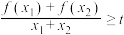 恒成立,则t的取值范围为( ).
恒成立,则t的取值范围为( ).A.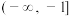 | B.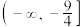 |
C. | D.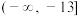 |
您最近一年使用:0次
2024-02-05更新
|
1022次组卷
|
9卷引用:5.3.2课时2函数的最大(小)值 第三练 能力提升拔高
(已下线)5.3.2课时2函数的最大(小)值 第三练 能力提升拔高(已下线)第六章:导数章末重点题型复习(3)(已下线)专题01 一元函数的导数及其应用-4江苏省东台市2023-2024学年高二上学期期末数学试题(已下线)专题4 导数在不等式中的应用(B)湖南省株洲市第一中学2021-2022学年高二上学期期末数学试题江苏省南通市海门中学2023-2024学年高二下学期3月学情调研数学试题(已下线)模块一 专题4 《导数在不等式中的应用》B提升卷(苏教版)(已下线)模块一 专题4 《导数在不等式中的应用》A基础卷(苏教版)
名校
3 . 已知 ,若存在实数
,若存在实数 (
(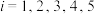 ),当
),当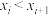 (
(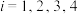 )时,满足
)时,满足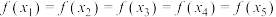 ,则
,则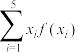 的取值范围为( )
的取值范围为( )
 ,若存在实数
,若存在实数 (
(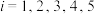 ),当
),当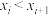 (
(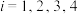 )时,满足
)时,满足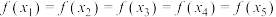 ,则
,则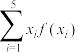 的取值范围为( )
的取值范围为( )A.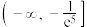 | B. |
C. | D.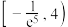 |
您最近一年使用:0次
2024-01-12更新
|
837次组卷
|
6卷引用:【一题多变】函数零点问题
(已下线)【一题多变】函数零点问题(已下线)【一题多变】函数零点问题1(已下线)2024年高考数学二轮复习测试卷(新高考Ⅰ卷专用)(已下线)第07讲 函数与方程(十一大题型)(讲义)-2陕西省渭南市2023-2024学高三上学期教学质量检测一(一模)文科数学试题湖南省株洲市第二中学2023-2024学年高三下学期开学考试数学试卷
名校
解题方法
4 . 若关于 的不等式
的不等式 对任意的
对任意的 恒成立,则
恒成立,则 的最小值为( )
的最小值为( )
 的不等式
的不等式 对任意的
对任意的 恒成立,则
恒成立,则 的最小值为( )
的最小值为( )A. | B.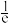 | C.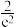 | D. |
您最近一年使用:0次
2023-11-26更新
|
742次组卷
|
4卷引用:第2讲:利用导数研究函数的性质【讲】高三清北学霸150分晋级必备
(已下线)第2讲:利用导数研究函数的性质【讲】高三清北学霸150分晋级必备(已下线)第三章 第四节 导数与不等式(讲-基础版)四川省2024届高三上学期第二次联考(月考)数学(文)试题福建省莆田二中、仙游一中、仙游金石中学、哲理中学2023-2024学年高二上学期期末联考数学试卷
名校
解题方法
5 . 已知函数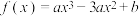 ,其中实数
,其中实数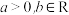 ,则下列结论正确的是( )
,则下列结论正确的是( )
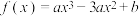 ,其中实数
,其中实数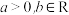 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 必有两个极值点 必有两个极值点 |
B. 有且仅有3个零点时, 有且仅有3个零点时, 的范围是 的范围是 |
C.当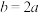 时,点 时,点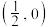 是曲线 是曲线 的对称中心 的对称中心 |
D.当 时,过点 时,过点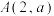 可以作曲线 可以作曲线 的3条切线 的3条切线 |
您最近一年使用:0次
2023-01-17更新
|
1184次组卷
|
8卷引用:模块四 期中重组篇(高二下浙江)
名校
6 . 若函数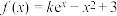 有三个零点,则k的取值范围为( )
有三个零点,则k的取值范围为( )
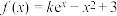 有三个零点,则k的取值范围为( )
有三个零点,则k的取值范围为( )A.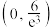 | B.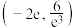 | C.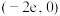 | D.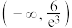 |
您最近一年使用:0次
2022-12-12更新
|
3058次组卷
|
10卷引用:专题2 数形结合思想
(已下线)专题2 数形结合思想(已下线)专题11 函数的零点-3陕西省安康市2023届高三上学期12月一模理科数学试题陕西省安康市2023届高三上学期12月一模文科数学试题黑龙江省哈尔滨师范大学附属中学2022-2023学年高二上学期期末考试数学试题四川省泸州高级中学校2022-2023学年高二下学期第一次质量检测文科数学试题1.3.2函数极值与导数—1.3.4导数的应用举例 (提高篇)贵州省兴义市顶效开发区顶兴学校2024届高三上学期第一次月考数学试题广东省东莞市七校2023-2024学年高二下学期5月联考数学试题广东省汕头市潮阳黄图盛中学2023-2024学年高二下学期第二次阶段考试数学试题
名校
解题方法
7 . 已知函数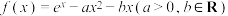 .
.
(1)若 ,
, ,试证明:当
,试证明:当 时,
时, ;
;
(2)若对任意 ,
, 均有两个极值点
均有两个极值点 ,
,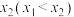 .
.
①求 应满足的条件;
应满足的条件;
②当 时,证明:
时,证明: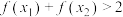 .
.
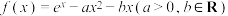 .
.(1)若
 ,
, ,试证明:当
,试证明:当 时,
时, ;
;(2)若对任意
 ,
, 均有两个极值点
均有两个极值点 ,
,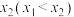 .
.①求
 应满足的条件;
应满足的条件;②当
 时,证明:
时,证明: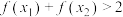 .
.
您最近一年使用:0次
2021-01-19更新
|
422次组卷
|
3卷引用:第八章 利用导数证明不等式 专题六 双变量不等式证法之换元法 微点2 双变量不等式证法之换元法(二)
(已下线)第八章 利用导数证明不等式 专题六 双变量不等式证法之换元法 微点2 双变量不等式证法之换元法(二)江苏省泰州姜堰中学2018—2019学年第一学期高三数学期中试题湖南省衡阳市第八中学2020-2021学年高三上学期1月第五次月考数学试题
名校
8 . 已知函数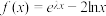 .
.
(1)当 时,求
时,求 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(2)当 时,判断
时,判断 的零点个数并说明理由;
的零点个数并说明理由;
(3)若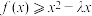 恒成立,求
恒成立,求 的取值范围.
的取值范围.
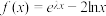 .
.(1)当
 时,求
时,求 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)当
 时,判断
时,判断 的零点个数并说明理由;
的零点个数并说明理由;(3)若
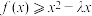 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-11-14更新
|
1765次组卷
|
7卷引用:考点11 导数的应用-备战2022年高考数学一轮复习考点帮(浙江专用)
(已下线)考点11 导数的应用-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)专题3-6 利用导函数研究方程的根(函数的零点)-2河北省保定市2021届高三上学期10月摸底考试数学试题河北省廊坊市2021届高三上学期摸底数学试题辽宁省沈阳市东北育才双语学校2023届高三上学期数学学科第一次模拟测试题广东省肇庆市封开县江口中学2023-2024学年高二下学期5月期中考试数学试题河南省南阳市第一中学校2024-2025学年高三上学期第二次月考数学试题
名校
解题方法
9 . 已知函数 在
在 上可导且
上可导且 ,其导函数
,其导函数 满足
满足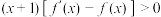 ,对于函数
,对于函数 ,下列结论正确的是( )
,下列结论正确的是( )
 在
在 上可导且
上可导且 ,其导函数
,其导函数 满足
满足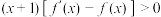 ,对于函数
,对于函数 ,下列结论正确的是( )
,下列结论正确的是( )A.函数 在 在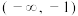 上为增函数 上为增函数 | B. 是函数 是函数 的极小值点 的极小值点 |
C.函数 必有2个零点 必有2个零点 | D.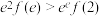 |
您最近一年使用:0次
2020-10-30更新
|
3061次组卷
|
19卷引用:专题04函数与导数(测)-2021年高考数学二轮复习讲练测(新高考版)
(已下线)专题04函数与导数(测)-2021年高考数学二轮复习讲练测(新高考版)(已下线)2021届高三高考数学适应性测试八省联考考后仿真系列卷二(已下线)专题01 《导数及其应用》中的典型题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) (已下线)第03讲 导数与函数的极值、最值(七大题型)(练习)湖南省郴州市2020-2021学年高三上学期第一次教学质量监测数学试题湖南省郴州市2021届高三第一次质检数学试题(已下线)期中模拟考试题(B卷能力篇)-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第三册)江苏省四中2020-2021学年高二下学期期中数学试题江苏省镇江市扬中市第二高级中学2021届高三下学期期初开学考试数学试题广东省湛江市第二高级中学2021届高三下学期3月模拟数学试题江苏省南通市西亭高级中学2020-2021学年高三上学期期中数学试题江苏省苏州市高新区第一中学2021-2022学年高二下学期期中数学试题黑龙江省牡丹江市第一高级中学2021-2022学年高二下学期4月月考数学试题重庆市江津第五中学校2021-2022学年高二下学期期中数学试题辽宁省鞍山市第三中学、华育高级中学2021-2022学年高二下学期期中考试数学试题江苏省无锡市堰桥高级中学2022-2023学年高三上学期10月月考数学试题重庆市璧山来凤中学2022-2023学年高二下学期第一次月考数学试题广东省潮州市2023届高三模拟数学试题广东佛山市南海区桂城中学2024届高三上学期1月调研考试数学试题
名校
解题方法
10 . 设函数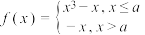 ,若
,若 无最大值,则实数
无最大值,则实数 的取值范围为
的取值范围为______ .
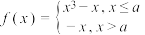 ,若
,若 无最大值,则实数
无最大值,则实数 的取值范围为
的取值范围为
您最近一年使用:0次
2020-10-09更新
|
628次组卷
|
4卷引用:专题01 《导数及其应用》中的典型题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)
(已下线)专题01 《导数及其应用》中的典型题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 浙江省温州市龙湾中学2019-2020学年高三下学期3月月考数学试题江西省上高二中2021届高三上学期第二次月考数学(理)试题江西省宜春市上高二中2021届高三(上)第二次月考数学(理科)试题



