名校
1 . 若存在常数  ,使得对定义域
,使得对定义域  内的任意
内的任意 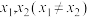 ,都有
,都有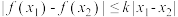 成立,则称函数
成立,则称函数  在其定义域
在其定义域  上是 "
上是 "  -利普希兹条件函数".
-利普希兹条件函数".
(1)判断函数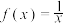 是否是区间
是否是区间  上的" 1 -利普希兹条件函数"?并说明理由;
上的" 1 -利普希兹条件函数"?并说明理由;
(2)已知函数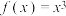 是区间
是区间 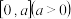 上的"3-利普希兹条件函数", 求实数
上的"3-利普希兹条件函数", 求实数  的取值范围;
的取值范围;
(3)若函数 为连续函数,其导函数为
为连续函数,其导函数为 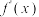 ,若
,若 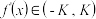 ,其中
,其中 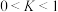 , 且
, 且 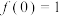 . 定义数列
. 定义数列 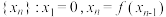 , 证明:
, 证明: 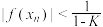 .
.
 ,使得对定义域
,使得对定义域  内的任意
内的任意 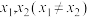 ,都有
,都有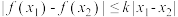 成立,则称函数
成立,则称函数  在其定义域
在其定义域  上是 "
上是 "  -利普希兹条件函数".
-利普希兹条件函数".(1)判断函数
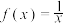 是否是区间
是否是区间  上的" 1 -利普希兹条件函数"?并说明理由;
上的" 1 -利普希兹条件函数"?并说明理由;(2)已知函数
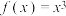 是区间
是区间 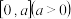 上的"3-利普希兹条件函数", 求实数
上的"3-利普希兹条件函数", 求实数  的取值范围;
的取值范围;(3)若函数
 为连续函数,其导函数为
为连续函数,其导函数为 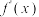 ,若
,若 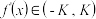 ,其中
,其中 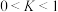 , 且
, 且 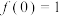 . 定义数列
. 定义数列 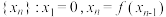 , 证明:
, 证明: 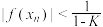 .
.
您最近一年使用:0次
2024-08-30更新
|
562次组卷
|
3卷引用:河北省衡水市衡水中学2025届高三上学期综合素质评价二数学试题
名校
2 . 以下不等式成立的是( )
A.当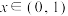 时, 时,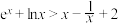 | B.当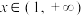 时, 时,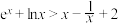 |
C.当 时, 时,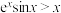 | D.当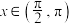 时, 时,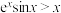 |
您最近一年使用:0次
名校
解题方法
3 . 凸函数是数学中一个值得研究的分支,它包括数学中大多数重要的函数,如 ,
, 等.记
等.记 为
为 的导数.现有如下定理:在区间I上
的导数.现有如下定理:在区间I上 为凸函数的充要条件为
为凸函数的充要条件为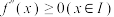 .
.
(1)证明:函数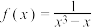 为
为 上的凸函数;
上的凸函数;
(2)已知函数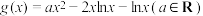 .
.
①若 为
为 上的凸函数,求
上的凸函数,求 的最小值;
的最小值;
②在①的条件下,当 取最小值时,证明:
取最小值时,证明: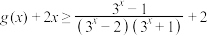 ,在
,在 上恒成立.
上恒成立.
 ,
, 等.记
等.记 为
为 的导数.现有如下定理:在区间I上
的导数.现有如下定理:在区间I上 为凸函数的充要条件为
为凸函数的充要条件为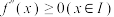 .
.(1)证明:函数
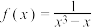 为
为 上的凸函数;
上的凸函数;(2)已知函数
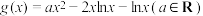 .
.①若
 为
为 上的凸函数,求
上的凸函数,求 的最小值;
的最小值;②在①的条件下,当
 取最小值时,证明:
取最小值时,证明: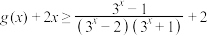 ,在
,在 上恒成立.
上恒成立.
您最近一年使用:0次
2024-09-28更新
|
568次组卷
|
3卷引用:河北省衡水市第二次调研考试2024-2025学年高三上学期9月月考数学试题
名校
4 . (1)求函数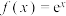 的图像在点
的图像在点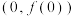 处的切线方程;
处的切线方程;
(2)证明: ;
;
(3)已知a,b,c均为正数,且 ,请证明:
,请证明: .
.
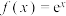 的图像在点
的图像在点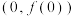 处的切线方程;
处的切线方程;(2)证明:
 ;
;(3)已知a,b,c均为正数,且
 ,请证明:
,请证明: .
.
您最近一年使用:0次
23-24高二下·江苏·开学考试
名校
解题方法
5 . 已知函数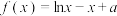 .
.
(1)若直线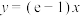 与函数
与函数 的图象相切,求实数
的图象相切,求实数 的值;
的值;
(2)若函数 有两个极值点
有两个极值点 和
和 ,且
,且 ,证明:
,证明: .(
.( 为自然对数的底数)
为自然对数的底数)
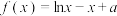 .
.(1)若直线
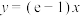 与函数
与函数 的图象相切,求实数
的图象相切,求实数 的值;
的值;(2)若函数
 有两个极值点
有两个极值点 和
和 ,且
,且 ,证明:
,证明: .(
.( 为自然对数的底数)
为自然对数的底数)
您最近一年使用:0次
2024-07-30更新
|
467次组卷
|
6卷引用:河北省衡水中学2024-2025学年高三上学期第一次综合素养测评数学试题
河北省衡水中学2024-2025学年高三上学期第一次综合素养测评数学试题(已下线)黄金卷08江苏省南京市第九中学2023-2024学年高三上学期12月月考数学试题(已下线)高二数学开学摸底考01(江苏专用)-2023-2024学年高中下学期开学摸底考试卷(已下线)专题4 导数在不等式中的应用(讲)(已下线)模块一 专题4 《导数在不等式中的应用》(苏教版)
名校
解题方法
6 . 已知 .
.
(1)求 的单调区间和最值;
的单调区间和最值;
(2)定理:若函数 在
在 上可导,在
上可导,在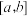 上连续,则存在
上连续,则存在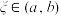 ,使得
,使得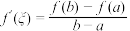 .该定理称为“拉格朗日中值定理”,请利用该定理解决下面问题:
.该定理称为“拉格朗日中值定理”,请利用该定理解决下面问题:
若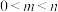 ,求证:
,求证: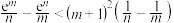 .
.
 .
.(1)求
 的单调区间和最值;
的单调区间和最值;(2)定理:若函数
 在
在 上可导,在
上可导,在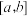 上连续,则存在
上连续,则存在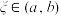 ,使得
,使得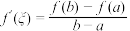 .该定理称为“拉格朗日中值定理”,请利用该定理解决下面问题:
.该定理称为“拉格朗日中值定理”,请利用该定理解决下面问题:若
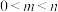 ,求证:
,求证: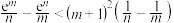 .
.
您最近一年使用:0次
解题方法
7 . 过点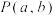 可以作曲线
可以作曲线 的两条切线,切点为
的两条切线,切点为 .
.
(1)证明: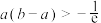 ;
;
(2)设线段 中点坐标为
中点坐标为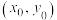 ,证明:
,证明: .
.
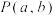 可以作曲线
可以作曲线 的两条切线,切点为
的两条切线,切点为 .
.(1)证明:
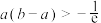 ;
;(2)设线段
 中点坐标为
中点坐标为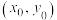 ,证明:
,证明: .
.
您最近一年使用:0次
名校
8 . 已知函数 有两个零点
有两个零点 ,且
,且 ,则下列命题正确的是( )
,则下列命题正确的是( )
 有两个零点
有两个零点 ,且
,且 ,则下列命题正确的是( )
,则下列命题正确的是( )A. | B. |
C.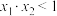 | D. |
您最近一年使用:0次
2024-05-20更新
|
834次组卷
|
3卷引用:河北省衡水市2024届高三下学期大数据应用调研联合测评( VIII)数学试题
名校
解题方法
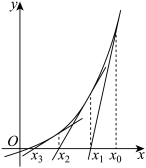
9 . 牛顿在《流数法》一书中,给出了代数方程的一种数值解法——牛顿法.具体做法如下:如图,设r是 的根,首先选取
的根,首先选取 作为r的初始近似值,若
作为r的初始近似值,若 在点
在点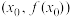 处的切线与
处的切线与 轴相交于点
轴相交于点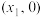 ,称
,称 是r的一次近似值;用
是r的一次近似值;用 替代
替代 重复上面的过程,得到
重复上面的过程,得到 ,称
,称 是r的二次近似值;一直重复,可得到一列数:
是r的二次近似值;一直重复,可得到一列数: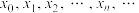 .在一定精确度下,用四舍五入法取值,当
.在一定精确度下,用四舍五入法取值,当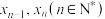 近似值相等时,该值即作为函数
近似值相等时,该值即作为函数 的一个零点
的一个零点 .
.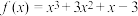 ,当
,当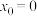 时,求方程
时,求方程 的二次近似值(保留到小数点后两位);
的二次近似值(保留到小数点后两位);
(2)牛顿法中蕴含了“以直代曲”的数学思想,直线常常取为曲线的切线或割线,求函数 在点
在点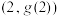 处的切线,并证明:
处的切线,并证明: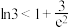 ;
;
(3)若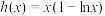 ,若关于
,若关于 的方程
的方程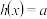 的两个根分别为
的两个根分别为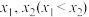 ,证明:
,证明: .
.
 的根,首先选取
的根,首先选取 作为r的初始近似值,若
作为r的初始近似值,若 在点
在点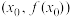 处的切线与
处的切线与 轴相交于点
轴相交于点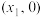 ,称
,称 是r的一次近似值;用
是r的一次近似值;用 替代
替代 重复上面的过程,得到
重复上面的过程,得到 ,称
,称 是r的二次近似值;一直重复,可得到一列数:
是r的二次近似值;一直重复,可得到一列数: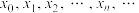 .在一定精确度下,用四舍五入法取值,当
.在一定精确度下,用四舍五入法取值,当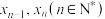 近似值相等时,该值即作为函数
近似值相等时,该值即作为函数 的一个零点
的一个零点 .
.
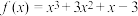 ,当
,当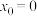 时,求方程
时,求方程 的二次近似值(保留到小数点后两位);
的二次近似值(保留到小数点后两位);(2)牛顿法中蕴含了“以直代曲”的数学思想,直线常常取为曲线的切线或割线,求函数
 在点
在点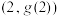 处的切线,并证明:
处的切线,并证明: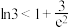 ;
;(3)若
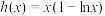 ,若关于
,若关于 的方程
的方程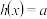 的两个根分别为
的两个根分别为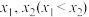 ,证明:
,证明: .
.
您最近一年使用:0次
2024-04-24更新
|
1668次组卷
|
8卷引用:河北省衡水市第二中学2024届高三高考模拟一数学试题
河北省衡水市第二中学2024届高三高考模拟一数学试题重庆市第八中学校2024届高三下学期高考强化训练(二)数学试题(已下线)情境1 源于教材阅读材料命题河北省衡水市第二中学2023-2024学年高二下学期5月学科素养检测(二调)数学试题(已下线)重难点突破04 双变量与多变量问题(七大题型)(已下线)重难点突破07 函数零点问题的综合应用(十大题型)-1(已下线)专题2 函数与导数新定义压轴大题(三)【讲】四川省成都列五中学2024-2025学年高三上学期入学摸底测试数学试题
名校
10 . 已知命题p: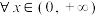 ,
, ,则( )
,则( )
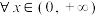 ,
, ,则( )
,则( )A.p是真命题, : : , , |
B.p是真命题, : : , , |
C.p是假命题, : : , , |
D.p是假命题, : : , , |
您最近一年使用:0次
2024-03-08更新
|
1330次组卷
|
4卷引用:河北省衡水市枣强县衡水董子高级中学2023-2024学年高三下学期3月月考数学试题



