名校
解题方法
1 . 已知等差数列 是单调递增数列,
是单调递增数列, ,且
,且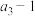 ,
, 成等比数列,
成等比数列, 是数列
是数列 的前
的前 项和.
项和.
(1)求数列 的通项公式;
的通项公式;
(2)设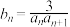 ,
, 是数列
是数列 的前
的前 项和,求满足
项和,求满足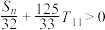 的最小的
的最小的 的值.
的值.
 是单调递增数列,
是单调递增数列, ,且
,且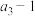 ,
, 成等比数列,
成等比数列, 是数列
是数列 的前
的前 项和.
项和.(1)求数列
 的通项公式;
的通项公式;(2)设
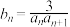 ,
, 是数列
是数列 的前
的前 项和,求满足
项和,求满足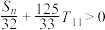 的最小的
的最小的 的值.
的值.
您最近一年使用:0次
2020-07-22更新
|
1081次组卷
|
3卷引用:甘肃省静宁县第一中学2020届高三第七次模拟考试数学(文)试题
名校
解题方法
2 . 设{an}是一个首项为2,公比为q(q 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且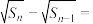 1(n≥2),求数列{an
1(n≥2),求数列{an bn}的前n项和Tn.
bn}的前n项和Tn.
 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且
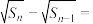 1(n≥2),求数列{an
1(n≥2),求数列{an bn}的前n项和Tn.
bn}的前n项和Tn.
您最近一年使用:0次
2020-06-08更新
|
1726次组卷
|
4卷引用:青海省海东市2020届高三第四次模拟考试数学(理)试题
3 . 已知等差数列 的公差为
的公差为 ,前
,前 项和为
项和为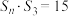 ,
, ,
, ,且______.从“①等比数列
,且______.从“①等比数列 的公比
的公比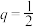 ,
, ,
, ;②
;② ,
,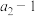 ,
,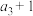 为等比数列
为等比数列 的前3项”这两个条件中,选择一个补充在上面问题中的划线部分,使得符合条件的数列
的前3项”这两个条件中,选择一个补充在上面问题中的划线部分,使得符合条件的数列 存在并作答.
存在并作答.
(1)求数列 的通项公式;
的通项公式;
(2)设数列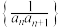 的前
的前 项和为
项和为 ,求证:
,求证: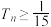 .
.
 的公差为
的公差为 ,前
,前 项和为
项和为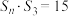 ,
, ,
, ,且______.从“①等比数列
,且______.从“①等比数列 的公比
的公比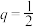 ,
, ,
, ;②
;② ,
,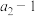 ,
,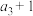 为等比数列
为等比数列 的前3项”这两个条件中,选择一个补充在上面问题中的划线部分,使得符合条件的数列
的前3项”这两个条件中,选择一个补充在上面问题中的划线部分,使得符合条件的数列 存在并作答.
存在并作答.(1)求数列
 的通项公式;
的通项公式;(2)设数列
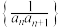 的前
的前 项和为
项和为 ,求证:
,求证: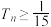 .
.
您最近一年使用:0次
4 .  为数列
为数列 的前
的前 项和.已知
项和.已知 ,
,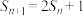 .
.
(1)证明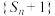 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)数列 为等差数列,且
为等差数列,且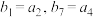 ,求数列
,求数列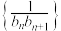 的前
的前 项和
项和 .
.
 为数列
为数列 的前
的前 项和.已知
项和.已知 ,
,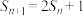 .
.(1)证明
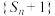 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;(2)数列
 为等差数列,且
为等差数列,且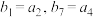 ,求数列
,求数列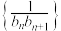 的前
的前 项和
项和 .
.
您最近一年使用:0次
2020-05-07更新
|
1321次组卷
|
3卷引用:宁夏银川市2019-2020学年普通高中高三学科教学质量检测理科数学试题
名校
解题方法
5 . 已知等差数列 ,若
,若 ,且
,且 ,
, ,
,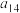 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,设
,设 ,求数列
,求数列 的前
的前 项和
项和 .
.
 ,若
,若 ,且
,且 ,
, ,
,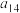 成等比数列.
成等比数列.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若
 ,设
,设 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2020-04-20更新
|
5462次组卷
|
8卷引用:湖北省襄阳五中、夷陵中学2019-2020学年高三下学期4月线上联合考试数学(理)试题
名校
解题方法
6 . 已知等差数列 的前
的前 项和为
项和为 ,等比数列
,等比数列 的前
的前 项和为
项和为 ,
, .
.
(1)若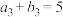 ,求
,求 的通项公式;
的通项公式;
(2)若 ,求
,求 .
.
 的前
的前 项和为
项和为 ,等比数列
,等比数列 的前
的前 项和为
项和为 ,
, .
.(1)若
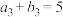 ,求
,求 的通项公式;
的通项公式;(2)若
 ,求
,求 .
.
您最近一年使用:0次
2020-08-25更新
|
2411次组卷
|
23卷引用:广东省惠东县惠东高级中学2018届高三适应性考试数学(文)试题
广东省惠东县惠东高级中学2018届高三适应性考试数学(文)试题河南省平顶山市郏县第一高级中学2017-2018学年高二上学期第三次月考数学(文)试题【全国百强校】宁夏育才中学2019届高三上学期月考二数学(文)试题2019届陕西省西安市第一中学高三上学期第一次月考数学(文)试题智能测评与辅导[文]-等比数列黑龙江省大庆实验中学2019-2020学年高二上学期开学考试数学(理)试题山东省青岛市第二中学2017-2018学年高一下学期期中数学试题广东省茂名市电白区2018-2019学年高二下学期期末数学(理)试题(已下线)专题14 数列综合-五年(2016-2020)高考数学(文)真题分项(已下线)专题18 等差数列与等比数列-十年(2011-2020)高考真题数学分项安徽省六安中学2019-2020学年高一下学期期末数学(文)试题陕西省咸阳市永寿中学2020-2021学年高三上学期开学考试数学(理)试题甘肃省玉门一中2020-2021学年高三第一次模拟考试文科数学试题广西南宁市第一中学2019-2020学年高二上学期期中段考数学试题山东省春季高考枣庄市2023届高三第二次模拟知识考试数学试题海南省陵水黎族自治县陵水中学2024届高三上学期第三次模拟测试数学试题(已下线)专题05 数列解答题(已下线)考向20等比数列及其前n项和(重点) - 3四川省达州市宣汉县土黄中学2022-2023学年高二上学期第一次测试数学试题(已下线)第03讲 等比数列及其前n项和 (高频考点—精讲)-2山东省菏泽第一中学2022-2023学年高二上学期12月月考数学试题(已下线)模块三 专题7 大题分类练(数列)基础夯实练 期末终极研习室(高二人教A版)(已下线)专题21 数列解答题(文科)-3
名校
7 . 给定数列 ,若数列
,若数列 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)已知数列 的通项公式为
的通项公式为 ,试判断
,试判断 是否为封闭数列,并说明理由;
是否为封闭数列,并说明理由;
(2)已知数列 满足
满足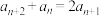 且
且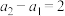 ,设
,设 是该数列
是该数列 的前
的前 项和,试问:是否存在这样的“封闭数列”
项和,试问:是否存在这样的“封闭数列” ,使得对任意
,使得对任意 都有
都有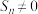 ,且
,且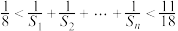 ,若存在,求数列
,若存在,求数列 的首项
的首项 的所有取值;若不存在,说明理由;
的所有取值;若不存在,说明理由;
(3)证明等差数列 成为“封闭数列”的充要条件是:存在整数
成为“封闭数列”的充要条件是:存在整数 ,使
,使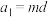 .
.
 ,若数列
,若数列 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.(1)已知数列
 的通项公式为
的通项公式为 ,试判断
,试判断 是否为封闭数列,并说明理由;
是否为封闭数列,并说明理由;(2)已知数列
 满足
满足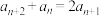 且
且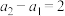 ,设
,设 是该数列
是该数列 的前
的前 项和,试问:是否存在这样的“封闭数列”
项和,试问:是否存在这样的“封闭数列” ,使得对任意
,使得对任意 都有
都有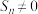 ,且
,且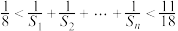 ,若存在,求数列
,若存在,求数列 的首项
的首项 的所有取值;若不存在,说明理由;
的所有取值;若不存在,说明理由;(3)证明等差数列
 成为“封闭数列”的充要条件是:存在整数
成为“封闭数列”的充要条件是:存在整数 ,使
,使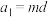 .
.
您最近一年使用:0次
2020-01-01更新
|
607次组卷
|
3卷引用:2018年上海市青浦区高三4月质量调研(二模)数学试题
名校
8 . 已知 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,都有
,都有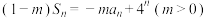 ;
;
(1)若 ,求证:数列
,求证:数列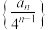 是等差数列,并求此时数列
是等差数列,并求此时数列 的通项公式;
的通项公式;
(2)若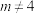 ,求证:数列
,求证:数列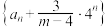 是等比数列,并求此时数列
是等比数列,并求此时数列 的通项公式;
的通项公式;
(3)设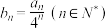 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,都有
,都有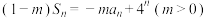 ;
;(1)若
 ,求证:数列
,求证:数列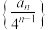 是等差数列,并求此时数列
是等差数列,并求此时数列 的通项公式;
的通项公式;(2)若
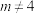 ,求证:数列
,求证:数列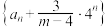 是等比数列,并求此时数列
是等比数列,并求此时数列 的通项公式;
的通项公式;(3)设
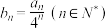 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2019-12-08更新
|
794次组卷
|
3卷引用:2018年上海市复旦附中高三5月三模数学试题
2018·上海浦东新·三模
名校
9 . 设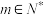 ,若无穷数列
,若无穷数列 满足:对所有整数
满足:对所有整数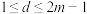 ,都成立
,都成立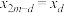 ,则称
,则称 “
“ -折叠数列”.
-折叠数列”.
(1)求所有的实数 ,使得通项公式为
,使得通项公式为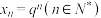 的数列
的数列 是
是 -折叠数列;
-折叠数列;
(2)给定常数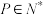 ,是否存在数列
,是否存在数列 ,使得对所有
,使得对所有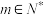 ,
, 都是
都是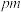 -折叠数列,且
-折叠数列,且 的各项中恰有
的各项中恰有 个不同的值?证明你的结论;
个不同的值?证明你的结论;
(3)设递增数列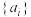 满足
满足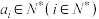 .已知如果对所有
.已知如果对所有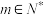 ,
, 都是
都是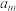 -折叠数列,则
-折叠数列,则 的各项中至多只有
的各项中至多只有 个不同的值,证明:
个不同的值,证明: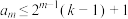 .
.
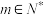 ,若无穷数列
,若无穷数列 满足:对所有整数
满足:对所有整数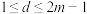 ,都成立
,都成立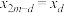 ,则称
,则称 “
“ -折叠数列”.
-折叠数列”.(1)求所有的实数
 ,使得通项公式为
,使得通项公式为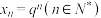 的数列
的数列 是
是 -折叠数列;
-折叠数列;(2)给定常数
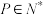 ,是否存在数列
,是否存在数列 ,使得对所有
,使得对所有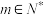 ,
, 都是
都是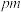 -折叠数列,且
-折叠数列,且 的各项中恰有
的各项中恰有 个不同的值?证明你的结论;
个不同的值?证明你的结论;(3)设递增数列
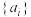 满足
满足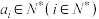 .已知如果对所有
.已知如果对所有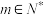 ,
, 都是
都是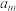 -折叠数列,则
-折叠数列,则 的各项中至多只有
的各项中至多只有 个不同的值,证明:
个不同的值,证明: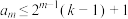 .
.
您最近一年使用:0次
17-18高一下·上海浦东新·期末
名校
10 . 如果一个数列从第2项起,每一项与它前一项的差都大于2,则称这个数列为“阿当数列”.
(1)若数列 为“阿当数列”,且
为“阿当数列”,且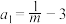 ,
,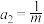 ,
, ,求实数
,求实数 的取值范围;
的取值范围;
(2)是否存在首项为1的等差数列 为“阿当数列”,且其前
为“阿当数列”,且其前 项和
项和 满足
满足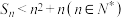 ?若存在,请求出
?若存在,请求出 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3)已知等比数列 的每一项均为正整数,且
的每一项均为正整数,且 为“阿当数列”,
为“阿当数列”,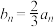 ,
,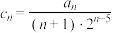 ,当数列
,当数列 不是“阿当数列”时,试判断数列
不是“阿当数列”时,试判断数列 是否为“阿当数列”,并说明理由.
是否为“阿当数列”,并说明理由.
(1)若数列
 为“阿当数列”,且
为“阿当数列”,且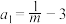 ,
,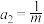 ,
, ,求实数
,求实数 的取值范围;
的取值范围;(2)是否存在首项为1的等差数列
 为“阿当数列”,且其前
为“阿当数列”,且其前 项和
项和 满足
满足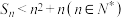 ?若存在,请求出
?若存在,请求出 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.(3)已知等比数列
 的每一项均为正整数,且
的每一项均为正整数,且 为“阿当数列”,
为“阿当数列”,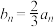 ,
,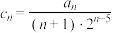 ,当数列
,当数列 不是“阿当数列”时,试判断数列
不是“阿当数列”时,试判断数列 是否为“阿当数列”,并说明理由.
是否为“阿当数列”,并说明理由.
您最近一年使用:0次



