1 . 公元前四世纪,毕达哥拉斯学派对数和形的关系进行了研究,他们借助几何图形(或格点)来表示数,称为形数,形数是联系算数和几何的纽带,下图为五角形数的前4个,现有如下说法:
①记所有的五角形数从小到大构成数列 ,则
,则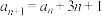 ;
;
②第9个五角形数比第8个五角形数多25;
③前8个五角形数之和为288;
④记所有的五角形数从小到大构成数列 ,则
,则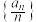 的前20项和为610;则正确的个数为( )
的前20项和为610;则正确的个数为( )
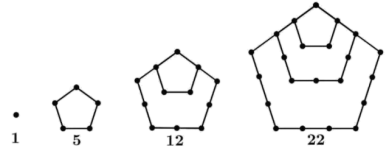
①记所有的五角形数从小到大构成数列
 ,则
,则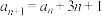 ;
;②第9个五角形数比第8个五角形数多25;
③前8个五角形数之和为288;
④记所有的五角形数从小到大构成数列
 ,则
,则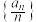 的前20项和为610;则正确的个数为( )
的前20项和为610;则正确的个数为( )
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
2022-01-11更新
|
292次组卷
|
3卷引用:吉林省白城市洮南市第一中学2022-2023学年高二下学期期中数学试题
吉林省白城市洮南市第一中学2022-2023学年高二下学期期中数学试题湖北省武汉市洪山高级中学2021-2022学年高二上学期12月月考数学试题(已下线)山东省济南市2022届高三二模数学试题变式题6-10
2 . 已知数列 满足
满足 ,
,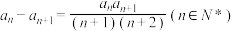 ,则
,则 的值为( )
的值为( )
 满足
满足 ,
,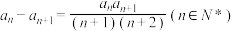 ,则
,则 的值为( )
的值为( )A. | B. | C.1 | D.2 |
您最近一年使用:0次
2021-11-06更新
|
592次组卷
|
2卷引用:吉林省通化市梅河口市第五中学2021-2022学年高二上学期期中数学试题
3 . 数列 满足
满足 ,对任意的
,对任意的 都有
都有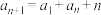 ,则
,则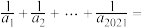
_____________ .
 满足
满足 ,对任意的
,对任意的 都有
都有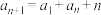 ,则
,则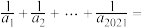
您最近一年使用:0次
2021-03-24更新
|
669次组卷
|
4卷引用:吉林省长春市第二实验中学2022-2023学年高二上学期期中数学试题
4 . 已知数列 的前
的前 项和为
项和为 ,且
,且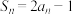 .
.
(1)求 的通项公式.
的通项公式.
(2)当 时,不等式
时,不等式 总成立,若
总成立,若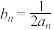 ,对任意正整数
,对任意正整数 ,
,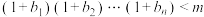 恒成立,求整数
恒成立,求整数 的最小值.
的最小值.
 的前
的前 项和为
项和为 ,且
,且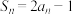 .
.(1)求
 的通项公式.
的通项公式.(2)当
 时,不等式
时,不等式 总成立,若
总成立,若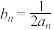 ,对任意正整数
,对任意正整数 ,
,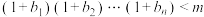 恒成立,求整数
恒成立,求整数 的最小值.
的最小值.
您最近一年使用:0次
5 . 数列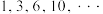 的一个通项公式是( )
的一个通项公式是( )
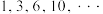 的一个通项公式是( )
的一个通项公式是( )A. | B.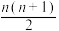 | C.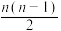 | D. |
您最近一年使用:0次



