名校
解题方法
1 . 19世纪的法国数学家卢卡斯以研究斐波那契数列而著名,以他的名字命名的卢卡斯数列 满足
满足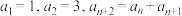 ,若其前
,若其前 项和为
项和为 ,则
,则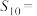 ( )
( )
 满足
满足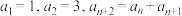 ,若其前
,若其前 项和为
项和为 ,则
,则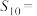 ( )
( )A.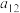 | B.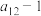 | C.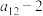 | D.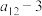 |
您最近一年使用:0次
2024-04-19更新
|
376次组卷
|
4卷引用:北师大版高二模块三专题1第2套小题进阶提升练
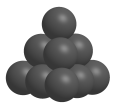
2 . 如图的形状出现在南宋数学家杨辉所著的《详解九章算法•商功》中,后人称为“三角垛”.“三角垛”最上层有1个球,第二层有3个球,第三层有6个球,……第 层有
层有 个球,则数列
个球,则数列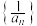 的前100项和为( )
的前100项和为( )
 层有
层有 个球,则数列
个球,则数列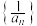 的前100项和为( )
的前100项和为( )
A.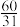 | B.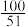 | C.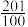 | D.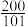 |
您最近一年使用:0次
2024-04-17更新
|
292次组卷
|
3卷引用:北师大版高二模块三专题1第3套小题入门夯实练
名校
解题方法
3 . 我国古代数学家沈括,杨辉,朱世杰等研究过二阶等差数列的相关问题.如果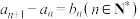 ,且数列
,且数列 为等差数列,那么数列
为等差数列,那么数列 为二阶等差数列.现有二阶等差数列的前4项依次为1,3,6,10,则该数列的第10项为
为二阶等差数列.现有二阶等差数列的前4项依次为1,3,6,10,则该数列的第10项为__________ .
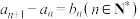 ,且数列
,且数列 为等差数列,那么数列
为等差数列,那么数列 为二阶等差数列.现有二阶等差数列的前4项依次为1,3,6,10,则该数列的第10项为
为二阶等差数列.现有二阶等差数列的前4项依次为1,3,6,10,则该数列的第10项为
您最近一年使用:0次
2023-12-11更新
|
623次组卷
|
7卷引用:模块一专题1《数列基础、等差数列和等比数列》单元检测篇A基础卷(高二人教B版)
(已下线)模块一专题1《数列基础、等差数列和等比数列》单元检测篇A基础卷(高二人教B版)(已下线)模块一 专题2《数列基础、等差数列和等比数列》单元检测篇A基础卷(高二北师大版)陕西省铜川阳光中学2021-2022学年高二上学期期末文科数学试题(已下线)模块一 专题5《等差数列与等比数列》单元检测篇 A基础卷 期末终极研习室(高二人教A版)广东省广州市执信中学2024届高三上学期大湾区数学冲刺卷(一)(已下线)1.2.1 等差数列的概念及其通项公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)黑龙江省齐齐哈尔市第八中学校2024届高三上学期1月大联考考后强化卷数学试题
解题方法
4 . 南宋数学家杨辉所著的《详解九章算法·商功》中出现了如图所示的形状,后人称为“三角垛”.“三角垛”的最上层(即第一层)有1个球,第二层有3个球,第三层有6个球,第四层有10个球,…,设“三角垛”从第一层到第n层的各层球的个数构成一个数列 ,则( )
,则( )
 ,则( )
,则( )
A. | B.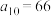 |
C. | D.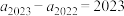 |
您最近一年使用:0次
5 . 高阶等差数列是数列逐项差数之差或高次差相等的数列,中国古代许多著名的数学家对推导高阶等差数列的求和公式很感兴趣,创造并发展了名为“垛积术”的算法,展现了聪明才智 如南宋数学家杨辉在《详解九章算法
如南宋数学家杨辉在《详解九章算法 商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关
商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关 如图是一个三角垛,最顶层有
如图是一个三角垛,最顶层有 个小球,第二层有
个小球,第二层有 个,第三层有
个,第三层有 个,第四层有
个,第四层有 个,则第
个,则第 层小球的个数为( )
层小球的个数为( )
 如南宋数学家杨辉在《详解九章算法
如南宋数学家杨辉在《详解九章算法 商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关
商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关 如图是一个三角垛,最顶层有
如图是一个三角垛,最顶层有 个小球,第二层有
个小球,第二层有 个,第三层有
个,第三层有 个,第四层有
个,第四层有 个,则第
个,则第 层小球的个数为( )
层小球的个数为( )
A. | B. | C. | D.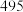 |
您最近一年使用:0次
2022-12-12更新
|
2752次组卷
|
21卷引用:北京市广渠门中学2022-2023学年高二下学期期中考试数学试题
北京市广渠门中学2022-2023学年高二下学期期中考试数学试题(已下线)模块四专题6重组综合练(四川)(8+3+3+5模式)(北师大版高二)(已下线)模块一专题2《数列的通项公式与求和》单元检测篇B提升卷(高二人教B版)(已下线)模块一 专题3《数列的通项公式与求和》单元检测篇B提升卷(高二北师大版)湖湘名校教育联合体五市十校教研教改共同体2023届高三第二次大联考数学试题(已下线)高考新题型-数列(已下线)技巧03 数学文化与数学阅读解题策略(精讲精练)-2广东省汕尾市城区汕尾中学2023届高三下学期第一次月考(期末)数学试题(已下线)专题4 数列广东省惠州市第一中学2022-2023学年高二下学期3月月考数学试题黑龙江省齐齐哈尔市第八中学校2022-2023学年高二下学期期中考试数学试题(已下线)专题10 数列通项公式的求法 微点10 数列通项公式的求法综合训练安徽省合肥市肥东县综合高中2022-2023学年高二下学期第一次月考(2月)数学试题江西省上饶市第一中学2022-2023学年高二下学期第一次月考(3月)数学试题(已下线)模块一 专题6《数列的通项公式与求和问题》单元检测篇 B提升卷(已下线)专题04 数列的概念与等差数列(1)四川省雅安市天立教育集团2023-2024学年高二下学期开学考试数学试题 广西桂林市田家炳中学2023-2024学年高二下学期期中测试数学试题湖北省襄阳市老河口市第一中学2022-2023学年高二上学期元月月考数学试题新疆石河子第一中学2022-2023学年高二下学期5月月考数学试题宁夏青铜峡市宁朔中学2024届高三上学期第四次月考数学(理)试题
6 . 南宋数学家杨辉在《详解九章算法》中论述了有关二阶等差数列的概念,它与一般的等差数列不同,相邻两项的差并不相等,但是逐项差数构成等差数列.例如,数列1,3,6,10,相邻两项的差组成新数列2,3,4,新数列2,3,4为等差数列,这样的数列称为二阶等差数列.现有二阶等差数列 ,则
,则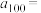
________ .
 ,则
,则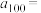
您最近一年使用:0次
2023-02-03更新
|
587次组卷
|
6卷引用:模块一专题2《数列的通项公式与求和》单元检测篇B提升卷(高二人教B版)
(已下线)模块一专题2《数列的通项公式与求和》单元检测篇B提升卷(高二人教B版)(已下线)模块一 专题3《数列的通项公式与求和》单元检测篇B提升卷(高二北师大版)安徽省阜阳市2022-2023学年高三上学期期末教学质量统测数学试题四川省绵阳中学2023届高三2月模拟检测理科数学试题上海市进才中学2022-2023学年高一下学期期末数学试题(已下线)模块一 专题6《数列的通项公式与求和问题》单元检测篇 B提升卷
7 . 已知数列 满足
满足 ,
, ,则
,则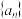 的通项公式
的通项公式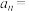 ( )
( )
 满足
满足 ,
, ,则
,则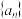 的通项公式
的通项公式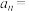 ( )
( )A.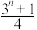 | B.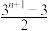 | C. | D.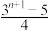 |
您最近一年使用:0次
2022-11-14更新
|
211次组卷
|
5卷引用:陕西省延安市2022-2023学年高二上学期期中理科数学试题
陕西省延安市2022-2023学年高二上学期期中理科数学试题陕西省西安市第七十五中学2022-2023学年高二上学期期中文科数学试题陕西省西安市第七十五中学2022-2023学年高二上学期期中理科数学试题(已下线)模块一 专题2 数列的通项公式与求和【讲】(高二下人教B版)(已下线)模块一 专题3 数列的通项公式与求和【讲】(高二下北师大版)
8 . 如图所示,用刀沿直线切一张圆形的薄饼,切1刀、2刀、3刀、4刀最多可以把饼分成2,4,7,11块,根据其中的规律,则切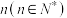 刀最多可以把饼分成
刀最多可以把饼分成______ 块.
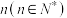 刀最多可以把饼分成
刀最多可以把饼分成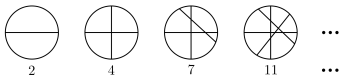
您最近一年使用:0次
2022-07-08更新
|
505次组卷
|
5卷引用:模块一专题1《数列基础、等差数列和等比数列》单元检测篇B提升卷(高二下人教B版)
(已下线)模块一专题1《数列基础、等差数列和等比数列》单元检测篇B提升卷(高二下人教B版)(已下线)模块一 专题2《数列基础、等差数列和等比数列》单元检测篇B提升卷(高二北师大版)河南省南阳市六校2021-2022学年高二下学期期末考试理科数学试题(已下线)专题10 数列通项公式的求法 微点10 数列通项公式的求法综合训练(已下线)模块一 专题5《等差数列与等比数列》单元检测篇 B提升卷 期末终极研习室(高二人教A版)
9 . 已知数列 中,
中, ,
, ,则数列
,则数列 的通项公式为( )
的通项公式为( )
 中,
中, ,
, ,则数列
,则数列 的通项公式为( )
的通项公式为( )A.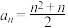 | B.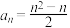 |
C.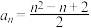 | D.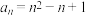 |
您最近一年使用:0次
2020-12-16更新
|
1213次组卷
|
5卷引用:北师大版高二模块三专题1第4套小题入门夯实练



