名校
解题方法
1 . 已知 是数列
是数列 的前n项和,且
的前n项和,且 ,则下列选项中正确的是( )
,则下列选项中正确的是( )
 是数列
是数列 的前n项和,且
的前n项和,且 ,则下列选项中正确的是( )
,则下列选项中正确的是( )A.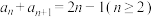 |
B. |
C.若 ,则 ,则 |
D.若数列 单调递增,则 单调递增,则 的取值范围是 的取值范围是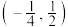 |
您最近一年使用:0次
7日内更新
|
329次组卷
|
2卷引用:江苏省“苏南十校联考”2025届高三10月联考数学试题
解题方法
2 . 对于一个给定的数列 ,令
,令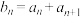 ,则数列
,则数列 称为数列
称为数列 的一阶和数列,再令
的一阶和数列,再令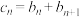 ,则数列
,则数列 是数列
是数列 的二阶和数列,以此类推,可得数列
的二阶和数列,以此类推,可得数列 的p阶和数列.
的p阶和数列.
(1)若 的二阶和数列是等比数列,且
的二阶和数列是等比数列,且 ,
, ,
, ,
,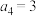 ,求
,求 ;
;
(2)若 ,求
,求 的二阶和数列的前n项和;
的二阶和数列的前n项和;
(3)若 是首项为1的等差数列,
是首项为1的等差数列, 是
是 的一阶和数列,且
的一阶和数列,且 ,
, ,求正整数k的最大值,以及k取最大值时
,求正整数k的最大值,以及k取最大值时 的公差.
的公差.
 ,令
,令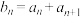 ,则数列
,则数列 称为数列
称为数列 的一阶和数列,再令
的一阶和数列,再令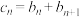 ,则数列
,则数列 是数列
是数列 的二阶和数列,以此类推,可得数列
的二阶和数列,以此类推,可得数列 的p阶和数列.
的p阶和数列.(1)若
 的二阶和数列是等比数列,且
的二阶和数列是等比数列,且 ,
, ,
, ,
,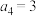 ,求
,求 ;
;(2)若
 ,求
,求 的二阶和数列的前n项和;
的二阶和数列的前n项和;(3)若
 是首项为1的等差数列,
是首项为1的等差数列, 是
是 的一阶和数列,且
的一阶和数列,且 ,
, ,求正整数k的最大值,以及k取最大值时
,求正整数k的最大值,以及k取最大值时 的公差.
的公差.
您最近一年使用:0次
3 . 已知等比数列 的首项
的首项 ,公比为q,记
,公比为q,记
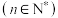 ,则“
,则“ ”是“数列
”是“数列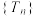 为递减数列”的( )
为递减数列”的( )
 的首项
的首项 ,公比为q,记
,公比为q,记
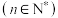 ,则“
,则“ ”是“数列
”是“数列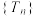 为递减数列”的( )
为递减数列”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
4 . 函数是数学中重要的概念之一,1692年,德国数学家莱布尼茨首次使用function这个词,1734年瑞士数学家欧拉首次使用符号 表示函数.1859年我国清代数学家李善兰将function译作函数,“函”意味着信件,巧妙地揭示了对应关系.密码学中的加密和解密其实就是函数与反函数.对自变量恰当地赋值是处理函数问题,尤其是处理抽象函数问题的常用方法之一.已知对任意的整数
表示函数.1859年我国清代数学家李善兰将function译作函数,“函”意味着信件,巧妙地揭示了对应关系.密码学中的加密和解密其实就是函数与反函数.对自变量恰当地赋值是处理函数问题,尤其是处理抽象函数问题的常用方法之一.已知对任意的整数 均有
均有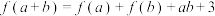 ,且
,且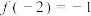 ,则
,则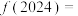
__________ .
 表示函数.1859年我国清代数学家李善兰将function译作函数,“函”意味着信件,巧妙地揭示了对应关系.密码学中的加密和解密其实就是函数与反函数.对自变量恰当地赋值是处理函数问题,尤其是处理抽象函数问题的常用方法之一.已知对任意的整数
表示函数.1859年我国清代数学家李善兰将function译作函数,“函”意味着信件,巧妙地揭示了对应关系.密码学中的加密和解密其实就是函数与反函数.对自变量恰当地赋值是处理函数问题,尤其是处理抽象函数问题的常用方法之一.已知对任意的整数 均有
均有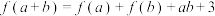 ,且
,且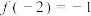 ,则
,则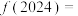
您最近一年使用:0次
7日内更新
|
292次组卷
|
4卷引用:吉林省白城市通榆县毓才高级中学2024-2025学年高三上学期第一次月考数学(理科)试卷
5 . 已知数列 的前
的前 项和为
项和为 ,且
,且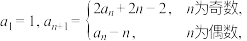 则
则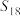 的值为( )
的值为( )
 的前
的前 项和为
项和为 ,且
,且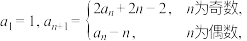 则
则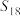 的值为( )
的值为( )| A.1023 | B.1461 | C.1533 | D.1955 |
您最近一年使用:0次
6 . 已知数列  ,记集合
,记集合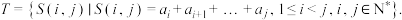
(1)若 ,当
,当 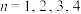 ,即
,即  时,写出集合
时,写出集合  ;
;
(2)若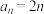 ,是否存在
,是否存在 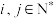 ,使得
,使得 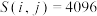 ? 若存在,求出一组符合条件的
? 若存在,求出一组符合条件的 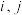 ; 若不存在,说明理由;
; 若不存在,说明理由;
(3)若 ,把集合
,把集合  中的元素从小到大排列,得到的新数列为:
中的元素从小到大排列,得到的新数列为: 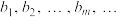 ,若
,若 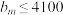 ,求
,求 的最大值.
的最大值.
 ,记集合
,记集合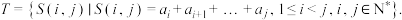
(1)若
 ,当
,当 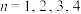 ,即
,即  时,写出集合
时,写出集合  ;
;(2)若
 ,是否存在
,是否存在 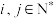 ,使得
,使得 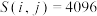 ? 若存在,求出一组符合条件的
? 若存在,求出一组符合条件的 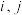 ; 若不存在,说明理由;
; 若不存在,说明理由;(3)若
 ,把集合
,把集合  中的元素从小到大排列,得到的新数列为:
中的元素从小到大排列,得到的新数列为: 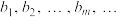 ,若
,若 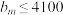 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
7 . 已知数列 满足
满足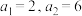 ,且
,且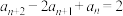 ,若
,若 表示不超过
表示不超过 的最大整数(例如
的最大整数(例如 ,记
,记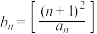 ,则数列
,则数列 的前2024项和为
的前2024项和为__________ .
 满足
满足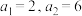 ,且
,且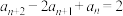 ,若
,若 表示不超过
表示不超过 的最大整数(例如
的最大整数(例如 ,记
,记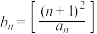 ,则数列
,则数列 的前2024项和为
的前2024项和为
您最近一年使用:0次
2024-11-03更新
|
133次组卷
|
2卷引用:甘肃省西北师范大学附属中学2024-2025学年高二上学期期中考试数学试题
名校
解题方法
8 . 已知等差数列 的首项为
的首项为 ,公差为
,公差为 ,前
,前 项和为
项和为 ,若
,若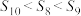 ,则下列说法正确的是( )
,则下列说法正确的是( )
 的首项为
的首项为 ,公差为
,公差为 ,前
,前 项和为
项和为 ,若
,若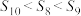 ,则下列说法正确的是( )
,则下列说法正确的是( )A.当 时, 时, 最大 最大 |
B.使得 成立的最小自然数 成立的最小自然数 |
C.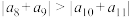 |
D.数列 中最小项为 中最小项为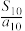 |
您最近一年使用:0次
9 . 已知整数 ,数列
,数列 是递增的整数数列,即
是递增的整数数列,即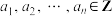 且
且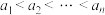 .数列
.数列 满足
满足 ,
, .若对于
.若对于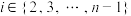 ,恒有
,恒有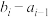 等于同一个常数
等于同一个常数 ,则称数列
,则称数列 为
为 的“左
的“左 型间隔数列”;若对于
型间隔数列”;若对于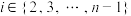 ,恒有
,恒有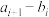 等于同一个常数
等于同一个常数 ,则称数列
,则称数列 为
为 的“右
的“右 型间隔数列”;若对于
型间隔数列”;若对于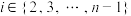 ,恒有
,恒有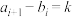 或者
或者 ,则称数列
,则称数列 为
为 的“左右
的“左右 型间隔数列”.
型间隔数列”.
(1)写出数列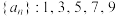 的所有递增的“左右1型间隔数列”;
的所有递增的“左右1型间隔数列”;
(2)已知数列 满足
满足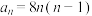 ,数列
,数列 是
是 的“左
的“左 型间隔数列”,数列
型间隔数列”,数列 是
是 的“右
的“右 型间隔数列”,若
型间隔数列”,若 ,且有
,且有 ,求
,求 的值;
的值;
(3)数列 是递增的整数数列,且
是递增的整数数列,且 ,
, .若存在
.若存在 的一个递增的“右4型间隔数列
的一个递增的“右4型间隔数列 ”,使得对于任意的
”,使得对于任意的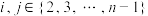 ,都有
,都有 ,求
,求 的关于
的关于 的最小值(即关于
的最小值(即关于 的最小值函数
的最小值函数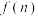 ).
).
 ,数列
,数列 是递增的整数数列,即
是递增的整数数列,即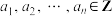 且
且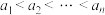 .数列
.数列 满足
满足 ,
, .若对于
.若对于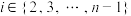 ,恒有
,恒有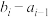 等于同一个常数
等于同一个常数 ,则称数列
,则称数列 为
为 的“左
的“左 型间隔数列”;若对于
型间隔数列”;若对于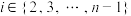 ,恒有
,恒有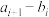 等于同一个常数
等于同一个常数 ,则称数列
,则称数列 为
为 的“右
的“右 型间隔数列”;若对于
型间隔数列”;若对于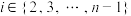 ,恒有
,恒有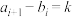 或者
或者 ,则称数列
,则称数列 为
为 的“左右
的“左右 型间隔数列”.
型间隔数列”.(1)写出数列
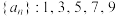 的所有递增的“左右1型间隔数列”;
的所有递增的“左右1型间隔数列”;(2)已知数列
 满足
满足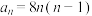 ,数列
,数列 是
是 的“左
的“左 型间隔数列”,数列
型间隔数列”,数列 是
是 的“右
的“右 型间隔数列”,若
型间隔数列”,若 ,且有
,且有 ,求
,求 的值;
的值;(3)数列
 是递增的整数数列,且
是递增的整数数列,且 ,
, .若存在
.若存在 的一个递增的“右4型间隔数列
的一个递增的“右4型间隔数列 ”,使得对于任意的
”,使得对于任意的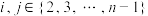 ,都有
,都有 ,求
,求 的关于
的关于 的最小值(即关于
的最小值(即关于 的最小值函数
的最小值函数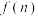 ).
).
您最近一年使用:0次
2024-10-31更新
|
509次组卷
|
2卷引用:浙江省强基联盟2024-2025学年高三上学期10月联考数学试卷
解题方法
10 . 已知数列 的首项为
的首项为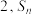 为数列
为数列 的前
的前 项和,
项和,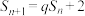 ,其中
,其中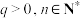 .
.
(1)若 是
是 和
和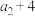 的等差中项,求数列
的等差中项,求数列 的通项公式;
的通项公式;
(2)在(1)的条件下,记集合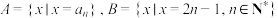 ,若将
,若将 所有元素从小到大依次排列构成一个新数列
所有元素从小到大依次排列构成一个新数列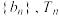 为数列
为数列 的前
的前 项和,求使得
项和,求使得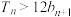 成立的
成立的 的最小值.
的最小值.
 的首项为
的首项为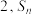 为数列
为数列 的前
的前 项和,
项和,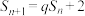 ,其中
,其中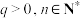 .
.(1)若
 是
是 和
和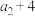 的等差中项,求数列
的等差中项,求数列 的通项公式;
的通项公式;(2)在(1)的条件下,记集合
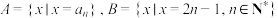 ,若将
,若将 所有元素从小到大依次排列构成一个新数列
所有元素从小到大依次排列构成一个新数列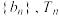 为数列
为数列 的前
的前 项和,求使得
项和,求使得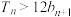 成立的
成立的 的最小值.
的最小值.
您最近一年使用:0次



