1 . 如图,已知 平面
平面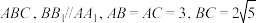 ,
,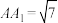 ,
,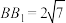 ,点
,点 为
为 的中点.
的中点.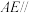 平面
平面 ;
;
(2)求直线 与平面
与平面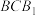 所成角的大小.
所成角的大小.
 平面
平面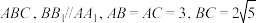 ,
,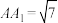 ,
,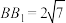 ,点
,点 为
为 的中点.
的中点.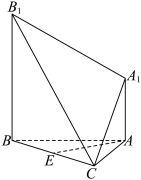
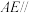 平面
平面 ;
;(2)求直线
 与平面
与平面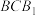 所成角的大小.
所成角的大小.
您最近一年使用:0次
2025高三·全国·专题练习
解题方法
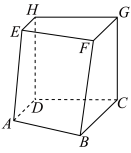
2 . 如图,空间六面体 中,
中,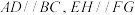 ,
,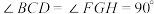 ,平面
,平面
 平面
平面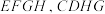 为正方形,平面
为正方形,平面 平面
平面 .求证:
.求证:

 ;
;
 中,
中,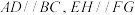 ,
,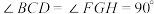 ,平面
,平面
 平面
平面 为正方形,平面
为正方形,平面 平面
平面 .求证:
.求证:

 ;
;
您最近一年使用:0次
解题方法
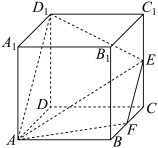
3 . 如图,在棱长均为2的四棱柱 中,点
中,点 是
是 的中点,
的中点, 交平面
交平面 于点
于点 .
.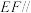 平面
平面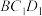 ;
;
(2)已知:条件①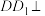 平面
平面 ,条件②
,条件② ,条件③平面
,条件③平面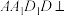 平面
平面 ,从这三个条件中选择两个作为已知,使得四棱柱
,从这三个条件中选择两个作为已知,使得四棱柱 存在且唯一确定,并求二面角
存在且唯一确定,并求二面角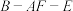 的余弦值.
的余弦值.
 中,点
中,点 是
是 的中点,
的中点, 交平面
交平面 于点
于点 .
.
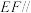 平面
平面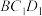 ;
;(2)已知:条件①
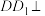 平面
平面 ,条件②
,条件② ,条件③平面
,条件③平面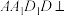 平面
平面 ,从这三个条件中选择两个作为已知,使得四棱柱
,从这三个条件中选择两个作为已知,使得四棱柱 存在且唯一确定,并求二面角
存在且唯一确定,并求二面角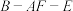 的余弦值.
的余弦值.
您最近一年使用:0次
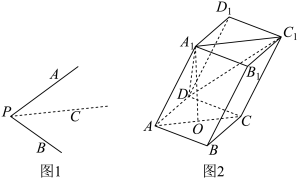
4 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理:如图1,由射线 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记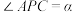 ,
,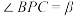 ,
, ,二面角
,二面角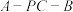 的大小为
的大小为 ,则
,则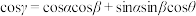 .如图2,四棱柱
.如图2,四棱柱 中,
中,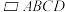 为菱形,
为菱形, ,
,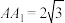 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.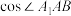 的值;
的值;
(2)直线 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: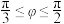 ;
;
(3)过点 作平面
作平面 ,使平面
,使平面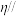 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记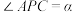 ,
,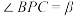 ,
, ,二面角
,二面角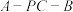 的大小为
的大小为 ,则
,则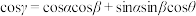 .如图2,四棱柱
.如图2,四棱柱 中,
中,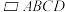 为菱形,
为菱形, ,
,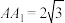 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.
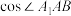 的值;
的值;(2)直线
 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: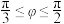 ;
;(3)过点
 作平面
作平面 ,使平面
,使平面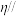 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
您最近一年使用:0次
2024-07-20更新
|
782次组卷
|
6卷引用:重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2
(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2(已下线)拔高点突破04 新情景、新定义下的立体几何问题(六大题型)-1山东省临沂市2023-2024学年高一下学期期末学科素养水平监测数学试题河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题山东省德州市夏津育中万隆中英文高级中学2024-2025学年高二上学期第一次月考数学试题
解题方法
5 . 如图,在六面体 中,
中, ,四边形
,四边形 是平行四边形,
是平行四边形,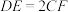 .
.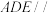 平面
平面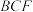 .
.
(2)若G是棱 的中点,证明:
的中点,证明: .
.
 中,
中, ,四边形
,四边形 是平行四边形,
是平行四边形,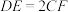 .
.
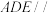 平面
平面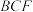 .
.(2)若G是棱
 的中点,证明:
的中点,证明: .
.
您最近一年使用:0次
2024-06-19更新
|
788次组卷
|
4卷引用:6.2 空间几何中的平行与垂直
(已下线)6.2 空间几何中的平行与垂直(已下线)第03讲 直线、平面平行的判定与性质(八大题型)(练习)广东省佛山市高明区2023-2024学年高一下学期5月月考数学试题海南省儋州黄冈实验学校2023-2024学年高一下学期期中考试数学试题
2024高一下·全国·专题练习
解题方法
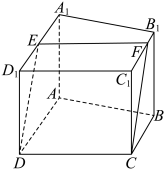
6 . 如图,直四棱柱 被平面
被平面 所截,截面为CDEF,且
所截,截面为CDEF,且 ,
,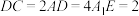 .证明:
.证明: .
.
 被平面
被平面 所截,截面为CDEF,且
所截,截面为CDEF,且 ,
,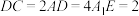 .证明:
.证明: .
.
您最近一年使用:0次
2024高一下·全国·专题练习
解题方法
7 . 如图,空间六面体 中,
中,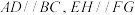 ,平面
,平面
 平面
平面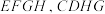 为正方形,求证:
为正方形,求证:

 ;
;
 中,
中,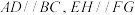 ,平面
,平面
 平面
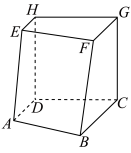
平面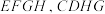 为正方形,求证:
为正方形,求证:

 ;
;
您最近一年使用:0次
2024高一下·全国·专题练习
解题方法
8 . 如图,在四棱锥 中,
中,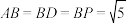 ,
,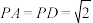 ,
,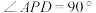 ,
, 、
、 分别是棱
分别是棱 ,
, 的中点,且
的中点,且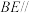 平面
平面 .证明:
.证明: .
.
 中,
中,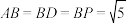 ,
,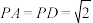 ,
,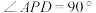 ,
, 、
、 分别是棱
分别是棱 ,
, 的中点,且
的中点,且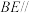 平面
平面 .证明:
.证明: .
.
您最近一年使用:0次
名校
9 . 如下左图,矩形 中,
中, ,
, ,
, .过顶点
.过顶点 作对角线
作对角线 的垂线,交对角线
的垂线,交对角线 于点
于点 ,交边
,交边 于点
于点 ,现将
,现将 沿
沿 翻折,形成四面体
翻折,形成四面体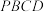 ,如下右图.
,如下右图.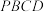 外接球的体积;
外接球的体积;
(2)求证:平面 平面
平面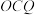 ;
;
(3)若点 为棱
为棱 的中点,请判断在将
的中点,请判断在将 沿
沿 翻折过程中,直线
翻折过程中,直线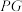 能否平行于面
能否平行于面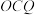 .若能请求出此时的二面角
.若能请求出此时的二面角 的大小;若不能,请说明理由.
的大小;若不能,请说明理由.
 中,
中, ,
, ,
, .过顶点
.过顶点 作对角线
作对角线 的垂线,交对角线
的垂线,交对角线 于点
于点 ,交边
,交边 于点
于点 ,现将
,现将 沿
沿 翻折,形成四面体
翻折,形成四面体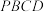 ,如下右图.
,如下右图.
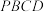 外接球的体积;
外接球的体积;(2)求证:平面
 平面
平面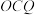 ;
;(3)若点
 为棱
为棱 的中点,请判断在将
的中点,请判断在将 沿
沿 翻折过程中,直线
翻折过程中,直线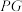 能否平行于面
能否平行于面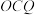 .若能请求出此时的二面角
.若能请求出此时的二面角 的大小;若不能,请说明理由.
的大小;若不能,请说明理由.
您最近一年使用:0次
2024-05-26更新
|
601次组卷
|
4卷引用:11.4.2 平面与平面垂直-【帮课堂】(人教B版2019必修第四册)
(已下线)11.4.2 平面与平面垂直-【帮课堂】(人教B版2019必修第四册)安徽省级示范高中培优联盟2023-2024学年高一下学期春季联赛数学试题安徽省亳州市第二完全中学2023-2024学年高一下学期第二次月考(5月)数学试题广东省湛江市2023-2024学年高一下学期期末调研测试数学试卷
名校
解题方法
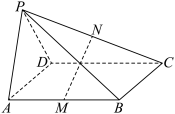
10 . 如图,四棱锥 的侧面
的侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 为矩形,且平面
为矩形,且平面 平面
平面 ,M,N分别为
,M,N分别为 的中点,直线PC与面
的中点,直线PC与面 所成角的正切值为
所成角的正切值为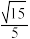 .
.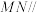 平面
平面 ;
;
(2)证明: .
.
 的侧面
的侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 为矩形,且平面
为矩形,且平面 平面
平面 ,M,N分别为
,M,N分别为 的中点,直线PC与面
的中点,直线PC与面 所成角的正切值为
所成角的正切值为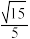 .
.
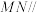 平面
平面 ;
;(2)证明:
 .
.
您最近一年使用:0次



