名校
解题方法
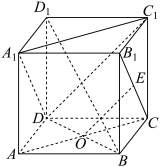
1 . 在棱长为1的正方体 中,
中,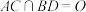 ,E是线段
,E是线段 (含端点)上的一动点,
(含端点)上的一动点,
① ;
;
②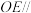 平面
平面 ;
;
③三棱锥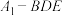 的体积为定值;
的体积为定值;
④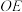 与
与 所成的最大角为
所成的最大角为 .
.
上述命题中正确的个数是( )
 中,
中,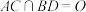 ,E是线段
,E是线段 (含端点)上的一动点,
(含端点)上的一动点,①
 ;
;②
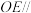 平面
平面 ;
;③三棱锥
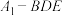 的体积为定值;
的体积为定值;④
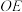 与
与 所成的最大角为
所成的最大角为 .
.上述命题中正确的个数是( )
| A.4 | B.3 | C.2 | D.1 |
您最近一年使用:0次
2024-07-15更新
|
728次组卷
|
4卷引用:天津市嘉诚中学2023-2024学年高一下学期期中质量调查数学试卷
名校
解题方法
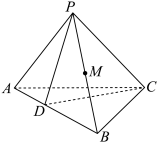
2 . 在三棱锥 中,
中, ,
,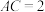 ,
,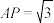 ,
, ,
, 的中点为
的中点为 ,点
,点 在线段
在线段 上,且满足
上,且满足 .
.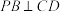 ;
;
(2)当平面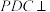 平面
平面 时,
时,
①求点 到平面
到平面 的距离;
的距离;
②若 为
为 的中点,求平面
的中点,求平面 与平面
与平面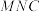 夹角的余弦值.
夹角的余弦值.
 中,
中, ,
,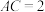 ,
,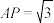 ,
, ,
, 的中点为
的中点为 ,点
,点 在线段
在线段 上,且满足
上,且满足 .
.
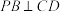 ;
;(2)当平面
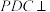 平面
平面 时,
时,①求点
 到平面
到平面 的距离;
的距离;②若
 为
为 的中点,求平面
的中点,求平面 与平面
与平面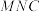 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2024-06-28更新
|
319次组卷
|
2卷引用:浙江省温州市十校联合体2023-2024学年高一下学期期中联考数学试题
名校
3 . 如图,矩形 中,
中, ,
, ,
, 为边
为边 的中点,沿
的中点,沿 将
将 折起,点
折起,点 折至
折至 处(
处(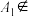 平面
平面 ),若
),若 为线段
为线段 的中点,平面
的中点,平面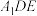 与平面
与平面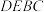 所成二面角
所成二面角 ,直线
,直线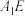 与平面
与平面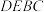 所成角为
所成角为 ,则在
,则在 折起的过程中,下列说法正确的是()
折起的过程中,下列说法正确的是()
 中,
中, ,
, ,
, 为边
为边 的中点,沿
的中点,沿 将
将 折起,点
折起,点 折至
折至 处(
处(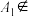 平面
平面 ),若
),若 为线段
为线段 的中点,平面
的中点,平面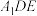 与平面
与平面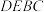 所成二面角
所成二面角 ,直线
,直线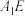 与平面
与平面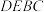 所成角为
所成角为 ,则在
,则在 折起的过程中,下列说法正确的是()
折起的过程中,下列说法正确的是()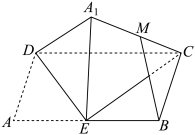
A.存在某个位置,使得 |
B. 面积的最大值为 面积的最大值为 |
C.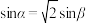 |
D.三棱锥 体积最大时,三棱锥 体积最大时,三棱锥 的外接球的表面积 的外接球的表面积 |
您最近一年使用:0次
解题方法
4 . 如图所示,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点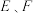 ,且
,且 ,给出下列判断:
,给出下列判断: 与
与 异面;②
异面;② 平面ABCD;③三棱锥
平面ABCD;③三棱锥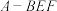 的体积为定值;④
的体积为定值;④ 的面积与
的面积与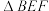 的面积相等;⑤
的面积相等;⑤ .其中判断正确的个数为( )
.其中判断正确的个数为( )
 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点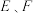 ,且
,且 ,给出下列判断:
,给出下列判断:
 与
与 异面;②
异面;② 平面ABCD;③三棱锥
平面ABCD;③三棱锥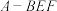 的体积为定值;④
的体积为定值;④ 的面积与
的面积与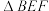 的面积相等;⑤
的面积相等;⑤ .其中判断正确的个数为( )
.其中判断正确的个数为( )| A.2 | B.3 | C.4 | D.5 |
您最近一年使用:0次
解题方法
5 . 如图,在多面体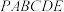 中,
中, 平面
平面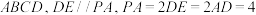 ,四边形
,四边形 是正方形,
是正方形, .
. 与平面
与平面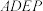 所成角的余弦值;
所成角的余弦值;
(2)证明: 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
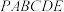 中,
中, 平面
平面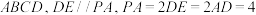 ,四边形
,四边形 是正方形,
是正方形, .
.
 与平面
与平面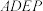 所成角的余弦值;
所成角的余弦值;(2)证明:
 平面
平面 ;
;(3)求三棱锥
 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
6 . 如图所示,在直三棱柱 中,若
中,若 ,
, ,则下列说法中正确的有( )
,则下列说法中正确的有( )
 中,若
中,若 ,
, ,则下列说法中正确的有( )
,则下列说法中正确的有( )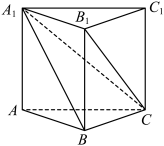
A.三棱锥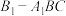 表面积为 表面积为 |
B.点 在线段 在线段 上运动,则 上运动,则 的最小值为 的最小值为 |
C. 、 、 分别为 分别为 、 、 的中点,过点 的中点,过点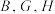 的平面截三棱柱 的平面截三棱柱 ,则该截面周长为 ,则该截面周长为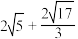 |
D.点 在侧面 在侧面 及其边界上运动,点 及其边界上运动,点 在棱 在棱 上运动,若直线 上运动,若直线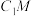 , , 是共面直线,则点 是共面直线,则点 的轨迹长度为 的轨迹长度为 |
您最近一年使用:0次
2024-06-21更新
|
999次组卷
|
3卷引用:黑龙江省佳木斯市第一中学2023-2024学年高一下学期5月期中考试数学试题
名校
7 . 如图,在四棱锥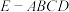 中,
中, 平面
平面 ,
,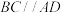 ,且
,且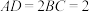 ,
, 是
是 的中点.
的中点. ;
;
(2)若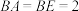 ,直线
,直线 与直线
与直线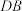 所成角的余弦值为
所成角的余弦值为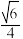 .
.
(ⅰ)求直线 与平面
与平面 所成角;
所成角;
(ⅱ)求二面角 的余弦值.
的余弦值.
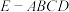 中,
中, 平面
平面 ,
,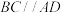 ,且
,且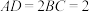 ,
, 是
是 的中点.
的中点.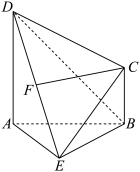
 ;
;(2)若
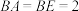 ,直线
,直线 与直线
与直线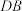 所成角的余弦值为
所成角的余弦值为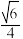 .
.(ⅰ)求直线
 与平面
与平面 所成角;
所成角;(ⅱ)求二面角
 的余弦值.
的余弦值.
您最近一年使用:0次
2024-06-18更新
|
1318次组卷
|
7卷引用:江苏省如皋市2023-2024学年高一下学期教学质量调研(二)数学试题
江苏省如皋市2023-2024学年高一下学期教学质量调研(二)数学试题(已下线)第24题 垂直的证明(高一期末每日一题)四川省泸州市江阳区2023-2024学年高一下学期6月期末数学试题宁夏回族自治区银川一中2023-2024学年高一下学期期末考试数学试卷安徽省六安第二中学河西校区2023-2024学年高一下学期6月期末考试数学试题(已下线)专题11 立体几何测试卷- 【暑假自学课】(沪教版2020)广西百色市平果市铝城中学2024-2025学年高二上学期开学收心考试数学试卷
名校
解题方法
8 . 如图,在棱长为 的正四面体
的正四面体 中,点
中,点 ,
, 分别为
分别为 和
和 的重心,
的重心, 为线段
为线段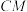 上一点.则下列结论正确的是( )
上一点.则下列结论正确的是( )
 的正四面体
的正四面体 中,点
中,点 ,
, 分别为
分别为 和
和 的重心,
的重心, 为线段
为线段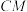 上一点.则下列结论正确的是( )
上一点.则下列结论正确的是( )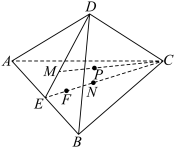
A.若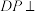 平面 平面 ,则 ,则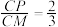 |
B.若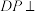 平面 平面 ,则三棱锥 ,则三棱锥 的体积为 的体积为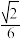 |
C.若 为线段 为线段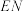 的中点,且 的中点,且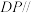 平面 平面 ,则 ,则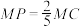 |
D. 的最小值为2 的最小值为2 |
您最近一年使用:0次
名校
解题方法
9 . 已知 、
、 为异面直线,
为异面直线,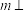 平面
平面 ,
,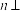 平面
平面 ,若直线
,若直线 满足
满足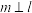 ,
, ,
, ,
,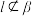 ,则( )
,则( )
 、
、 为异面直线,
为异面直线,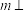 平面
平面 ,
,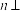 平面
平面 ,若直线
,若直线 满足
满足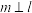 ,
, ,
, ,
,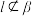 ,则( )
,则( )A.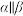 , ,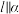 | B. , , |
C. 直线 直线 , ,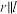 | D. 直线 直线 , , |
您最近一年使用:0次
名校
10 . 如下如图,水平桌面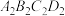 上放置一个透明塑料制成的长方体水槽
上放置一个透明塑料制成的长方体水槽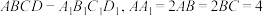 ,水面高度恰为长方体高的一半,在该长方体侧面
,水面高度恰为长方体高的一半,在该长方体侧面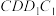 上有一个小孔
上有一个小孔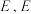 点到
点到 的距离为3.将该长方体水槽绕
的距离为3.将该长方体水槽绕 倾斜(
倾斜( 始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱
始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱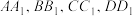 分别相交于点
分别相交于点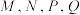 .
.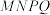 是矩形;
是矩形;
(2)当水恰好流出时,求二面角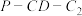 的大小.
的大小.
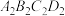 上放置一个透明塑料制成的长方体水槽
上放置一个透明塑料制成的长方体水槽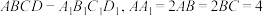 ,水面高度恰为长方体高的一半,在该长方体侧面
,水面高度恰为长方体高的一半,在该长方体侧面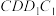 上有一个小孔
上有一个小孔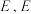 点到
点到 的距离为3.将该长方体水槽绕
的距离为3.将该长方体水槽绕 倾斜(
倾斜( 始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱
始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱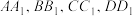 分别相交于点
分别相交于点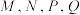 .
.
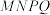 是矩形;
是矩形;(2)当水恰好流出时,求二面角
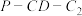 的大小.
的大小.
您最近一年使用:0次



