名校
1 . 如图所示的几何体 ABCDE 中,DA⊥平面 EAB ,AB=AD=AE=2BC=2,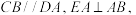 M是EC上的点(不与端点重合),F 为AD上的点,N 为BE的中点.
M是EC上的点(不与端点重合),F 为AD上的点,N 为BE的中点.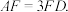
(i) 求证: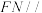 平面
平面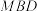
(ii) 求点F 到平面MBD的距离.
(2)若平面MBD与平面ABD所成角(锐角)的余弦值为 试确定点M在EC上的位置.
试确定点M在EC上的位置.
 M是EC上的点(不与端点重合),F 为AD上的点,N 为BE的中点.
M是EC上的点(不与端点重合),F 为AD上的点,N 为BE的中点.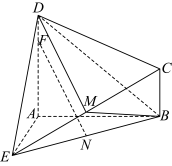
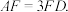
(i) 求证:
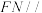 平面
平面
(ii) 求点F 到平面MBD的距离.
(2)若平面MBD与平面ABD所成角(锐角)的余弦值为
 试确定点M在EC上的位置.
试确定点M在EC上的位置.
您最近一年使用:0次
2023-12-18更新
|
247次组卷
|
4卷引用:天津市和平区耀华中学2023-2024学年高二上学期12月月考数学试题
天津市和平区耀华中学2023-2024学年高二上学期12月月考数学试题(已下线)第6章 空间向量与立体几何单元综合测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)江苏省扬州市广陵区红桥高级中学2023-2024学年高二下学期3月月考数学试题江苏省泰州市第三高级中学2023-2024学年高二下学期第一次阶段检测数学试卷
2 . 如图,在三棱台 中,
中,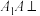 平面
平面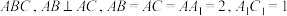 ,
, 为
为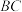 中点.,N为AB的中点,
中点.,N为AB的中点, //平面
//平面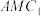 ;
;
(2)求平面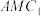 与平面
与平面 所成夹角的余弦值;
所成夹角的余弦值;
(3)求点 到平面
到平面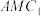 的距离.
的距离.
 中,
中,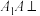 平面
平面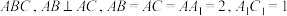 ,
, 为
为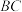 中点.,N为AB的中点,
中点.,N为AB的中点,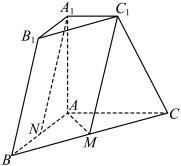
 //平面
//平面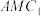 ;
;(2)求平面
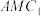 与平面
与平面 所成夹角的余弦值;
所成夹角的余弦值;(3)求点
 到平面
到平面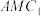 的距离.
的距离.
您最近一年使用:0次
2023-06-08更新
|
22268次组卷
|
29卷引用:天津市益中学校2023-2024学年高二上学期10月月考数学试题
天津市益中学校2023-2024学年高二上学期10月月考数学试题天津市和平区第二南开学校2023-2024学年高二上学期第三次月考数学试题2023年天津高考数学真题(已下线)第04讲 利用几何法解决空间角和距离19种常见考法归类(5)(已下线)第03讲 空间中平行、垂直问题10种常见考法归类(3)江苏省南通市海安市实验中学2022-2023学年高二下学期6月期末模拟数学试题专题06空间向量与立体几何(成品)(已下线)模块五 专题3 期末全真拔高模拟3江苏省南京市第二十九中学2022-2023学年高一下学期期末数学试题(已下线)2023年天津高考数学真题变式题16-20(已下线)第五篇 向量与几何 专题18 空间点线面问题 微点1 空间点线面问题江苏省徐州市邳州市新世纪学校2024届高三上学期统练1数学试题天津市第四十七中学2023-2024学年高三上学期第一次阶段性检测数学试题吉林省吉林市永吉县第四中学2023-2024学年高二上学期9月月考数学试题北京市东城区东直门中学2024届高三上学期期中数学试题天津市滨海新区塘沽第一中学2024届高三上学期第一次月考数学复习卷3(已下线)专题01 空间向量及其应用常考题型归纳(2)(已下线)模块7 空间几何篇 第2讲:立体几何的截面问题【练】专题12空间中直线、平面的平行与垂直关系(解答题)(已下线)专题7.2 空间中的位置关系【十大题型】(已下线)专题7.3 空间角与空间中的距离问题【九大题型】(已下线)专题15 立体几何解答题全归类(9大核心考点)(讲义)-1(已下线)重难点12 立体几何必考经典解答题全归类【九大题型】(已下线)专题06 立体几何 第二讲 立体几何中的计算问题(解密讲义)(已下线)题型20 6类立体几何大题解题技巧福建省福州第二中学2023-2024学年高二下学期第三学段(期中)考试数学试题(已下线)第33题 空间距离解法笃定,向量方法建系第一(优质好题一题多解)(已下线)专题23 立体几何解答题(理科)-3(已下线)专题23 立体几何解答题(文科)-3
3 . 已知正方体 的棱长为1,则点
的棱长为1,则点 到平面
到平面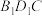 的距离为( )
的距离为( )
 的棱长为1,则点
的棱长为1,则点 到平面
到平面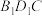 的距离为( )
的距离为( )A. | B. | C. | D. |
您最近一年使用:0次
名校
解题方法
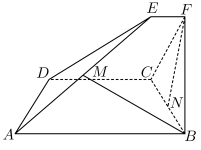
4 . 如图,已知 和
和 都是直角梯形,
都是直角梯形, ,
, ,
,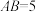 ,
, ,
,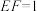 ,
,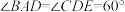 ,二面角
,二面角 的平面角为
的平面角为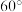 .设M,N分别为
.设M,N分别为 ,
, 的中点.
的中点.
(1)求证: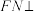 平面
平面 .
.
(2)求直线 与平面
与平面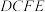 所成角的正弦值.
所成角的正弦值.
(3)求点D到平面 的距离.
的距离.
 和
和 都是直角梯形,
都是直角梯形, ,
, ,
,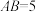 ,
, ,
,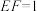 ,
,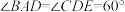 ,二面角
,二面角 的平面角为
的平面角为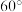 .设M,N分别为
.设M,N分别为 ,
, 的中点.
的中点.
(1)求证:
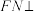 平面
平面 .
.(2)求直线
 与平面
与平面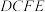 所成角的正弦值.
所成角的正弦值.(3)求点D到平面
 的距离.
的距离.
您最近一年使用:0次
名校
解题方法
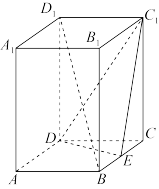
5 . 如图,在直四棱柱 中,侧棱
中,侧棱 的长为3,底面
的长为3,底面 是边长为2的正方形,
是边长为2的正方形, 是棱
是棱 的中点.
的中点.
(1)证明: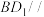 平面
平面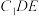 ;
;
(2)求平面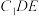 与平面
与平面 的夹角的正切值;
的夹角的正切值;
(3)求点 到平面
到平面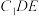 的距离.
的距离.
 中,侧棱
中,侧棱 的长为3,底面
的长为3,底面 是边长为2的正方形,
是边长为2的正方形, 是棱
是棱 的中点.
的中点.
(1)证明:
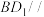 平面
平面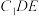 ;
;(2)求平面
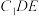 与平面
与平面 的夹角的正切值;
的夹角的正切值;(3)求点
 到平面
到平面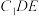 的距离.
的距离.
您最近一年使用:0次
2023-01-03更新
|
841次组卷
|
6卷引用:天津市和平区2022-2023学年高三上学期期末数学试题
名校
解题方法
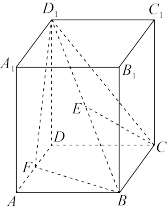
6 . 如图,正四棱柱 中,且
中,且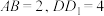 ,点
,点 分别是
分别是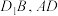 的中点.
的中点.
(1)求直线 与直线
与直线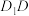 所成角的正切值;
所成角的正切值;
(2)求平面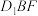 与平面
与平面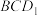 的夹角的余弦值;
的夹角的余弦值;
(3)求点 到平面
到平面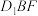 的距离.
的距离.
 中,且
中,且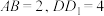 ,点
,点 分别是
分别是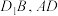 的中点.
的中点.
(1)求直线
 与直线
与直线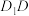 所成角的正切值;
所成角的正切值;(2)求平面
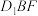 与平面
与平面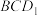 的夹角的余弦值;
的夹角的余弦值;(3)求点
 到平面
到平面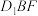 的距离.
的距离.
您最近一年使用:0次
2022-05-24更新
|
1154次组卷
|
2卷引用:天津市和平区2022届高三下学期三模数学试题
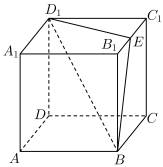
7 . 如图,已知正方体 的棱长为2,
的棱长为2, 的中点为E,则点
的中点为E,则点 到平面
到平面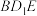 的距离为( )
的距离为( )
 的棱长为2,
的棱长为2, 的中点为E,则点
的中点为E,则点 到平面
到平面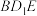 的距离为( )
的距离为( )
A. | B. | C. | D. |
您最近一年使用:0次
2022-02-08更新
|
780次组卷
|
3卷引用:天津市耀华中学2021-2022学年高一下学期期末数学试题
天津市耀华中学2021-2022学年高一下学期期末数学试题安徽省示范高中2021-2022学年高三上学期冬季联赛理科数学试题(已下线)广东省深圳市高级中学(集团)2023届高三上学期期末数学试题变式题6-10
8 . 如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB、PD的中点.若PA=AD=3,CD= .
.
(1)求证:AF 平面PCE;
平面PCE;
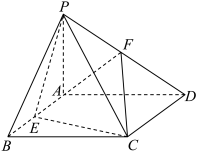
(2)求点F到平面PCE的距离;
(3)求直线FC与平面PCE所成角的正弦值.
 .
.(1)求证:AF
 平面PCE;
平面PCE;
(2)求点F到平面PCE的距离;
(3)求直线FC与平面PCE所成角的正弦值.
您最近一年使用:0次
2020-11-07更新
|
1726次组卷
|
8卷引用:天津市耀华中学2020-2021学年高二(上)第一次段考数学试题
名校
9 . 如图,在四棱锥 中,
中, 平面
平面 ,四边形
,四边形 是矩形,
是矩形,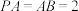 ,
,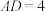 ,
, 是
是 的中点,
的中点, ,垂足为
,垂足为 .
.

(1)证明: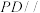 平面
平面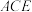 ;
;
(2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角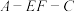 的正弦值.
的正弦值.
 中,
中, 平面
平面 ,四边形
,四边形 是矩形,
是矩形,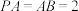 ,
,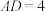 ,
, 是
是 的中点,
的中点, ,垂足为
,垂足为 .
.
(1)证明:
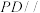 平面
平面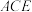 ;
;(2)求点
 到平面
到平面 的距离;
的距离;(3)求二面角
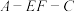 的正弦值.
的正弦值.
您最近一年使用:0次
2020-11-06更新
|
1223次组卷
|
4卷引用:天津市第一中学2020-2021学年高三上学期月考(一)数学试题
天津市第一中学2020-2021学年高三上学期月考(一)数学试题天津市天津一中2021届高三(上)第一次月考数学试题(已下线)2022年全国新高考Ⅰ卷数学试题变式题9-12题(已下线)2022年全国新高考Ⅰ卷数学试题变式题17-19题
10-11高三·重庆·阶段练习
10 . 如图,直二面角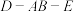 中,四边形ABCD是边长为2的正方形,
中,四边形ABCD是边长为2的正方形, ,F为CE上的点,且
,F为CE上的点,且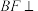 平面ACE.
平面ACE.
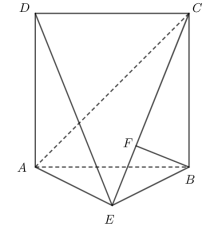
(1)求证 平面BCE;
平面BCE;
(2)求二面角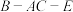 的大小;
的大小;
(3)求点D到平面ACE的距离.
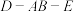 中,四边形ABCD是边长为2的正方形,
中,四边形ABCD是边长为2的正方形, ,F为CE上的点,且
,F为CE上的点,且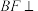 平面ACE.
平面ACE.
(1)求证
 平面BCE;
平面BCE;(2)求二面角
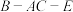 的大小;
的大小;(3)求点D到平面ACE的距离.
您最近一年使用:0次
2022-03-29更新
|
1163次组卷
|
13卷引用:天津市耀华中学2022届高三下学期统练12数学试题
天津市耀华中学2022届高三下学期统练12数学试题(已下线)2012届重庆市八中高三第二次月考文科数学福建省漳州市龙海市程溪中学2018-2019学年高二(上)期中考试数学(理科)试题(已下线)专题46 空间向量与立体几何大题解题模板-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题46 空间向量与立体几何大题解题模板-2021年高考一轮数学(理)单元复习一遍过(已下线)专题43 立体几何大题解题模板-2021年高考一轮数学(文)单元复习一遍过(已下线)第八单元 立体几何 (A卷 基础过关检测)-2021年高考数学(理)一轮复习单元滚动双测卷天津市南开区南大奥宇培训学校2020届高三下学期第三次月考数学试题(已下线)专题03 立体几何大题解题模板-(新教材)2020-2021学年高二数学单元复习(人教A版选择性必修第一册)(已下线)天津市南开中学2022届高三下学期二模数学试题(已下线)临考押题卷01-2022年高考数学临考押题卷(天津卷)2005年普通高等学校招生考试数学(理)试题(福建卷)2005年普通高等学校招生考试数学(文)试题(福建卷)



