1 . 已知四棱锥 中,底面
中,底面 是正方形,
是正方形, 平面
平面 ,
, ,
, 是
是 的中点.
的中点.
(2)求面ADE与面ABD所成角的大小;
 中,底面
中,底面 是正方形,
是正方形, 平面
平面 ,
, ,
, 是
是 的中点.
的中点.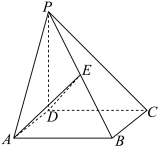
(2)求面ADE与面ABD所成角的大小;
您最近一年使用:0次
2 . 如图,在四棱锥 中,平面
中,平面 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
,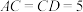 ,
, ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,平面
中,平面 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
,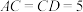 ,
,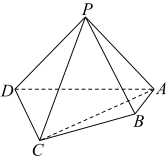
 ⊥平面
⊥平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
3 . 如图,已知四棱锥 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, 平面
平面 ,
, ,
, 分别是
分别是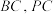 的中点.
的中点. 平面
平面 ;
;
(2)若 ,求二面角
,求二面角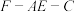 的余弦值.
的余弦值.
 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, 平面
平面 ,
, ,
, 分别是
分别是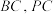 的中点.
的中点.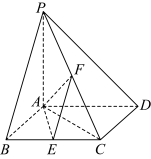
 平面
平面 ;
;(2)若
 ,求二面角
,求二面角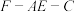 的余弦值.
的余弦值.
您最近一年使用:0次
4 . 已知三棱锥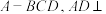 底面
底面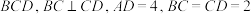 ,点
,点 是
是 的中点,点
的中点,点 为线段
为线段 上一动点,点
上一动点,点 在线段
在线段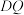 上.
上.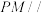 平面
平面 ,求证:
,求证: 为
为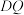 的中点;
的中点;
(2)若 为
为 的中点,求直线
的中点,求直线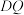 与平面
与平面 所成角的余弦值.
所成角的余弦值.
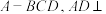 底面
底面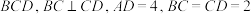 ,点
,点 是
是 的中点,点
的中点,点 为线段
为线段 上一动点,点
上一动点,点 在线段
在线段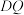 上.
上.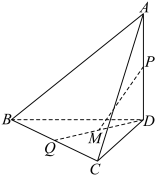
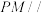 平面
平面 ,求证:
,求证: 为
为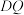 的中点;
的中点;(2)若
 为
为 的中点,求直线
的中点,求直线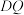 与平面
与平面 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
名校
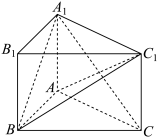
5 . 如图,在直三棱柱 中,
中, ,
, .
.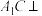 平面
平面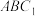 ;
;
(2)求直线 与
与 所成角的余弦值.
所成角的余弦值.
 中,
中, ,
, .
.
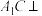 平面
平面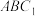 ;
;(2)求直线
 与
与 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
名校
解题方法
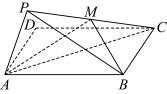
6 . 如图,在矩形纸片 中,
中, ,沿
,沿 将
将 折起,使点
折起,使点 到达点
到达点 的位置,且满足平面
的位置,且满足平面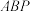 ⊥平面
⊥平面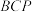 .
. 平面
平面 ,并求
,并求 的长度;
的长度;
(2)若 是线段
是线段 上(不包括端点)的一个动点,是否存在点
上(不包括端点)的一个动点,是否存在点 ,使得直线
,使得直线 与平面
与平面 的夹角为
的夹角为 ?若存在,求
?若存在,求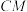 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
 中,
中, ,沿
,沿 将
将 折起,使点
折起,使点 到达点
到达点 的位置,且满足平面
的位置,且满足平面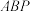 ⊥平面
⊥平面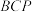 .
.
 平面
平面 ,并求
,并求 的长度;
的长度;(2)若
 是线段
是线段 上(不包括端点)的一个动点,是否存在点
上(不包括端点)的一个动点,是否存在点 ,使得直线
,使得直线 与平面
与平面 的夹角为
的夹角为 ?若存在,求
?若存在,求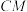 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
您最近一年使用:0次
解题方法
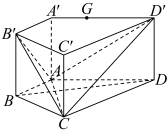
7 . 如图,在直四棱柱 中,
中,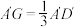 ,
, ,
, ,
, ,
,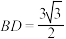 .
.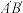 于点M,求线段
于点M,求线段 的长;
的长;
(2)若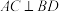 ,当二面角
,当二面角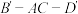 为直二面角时,求直四棱柱
为直二面角时,求直四棱柱 的体积.
的体积.
 中,
中, ,
, ,
, ,
, ,
,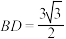 .
.
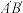 于点M,求线段
于点M,求线段 的长;
的长;(2)若
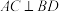 ,当二面角
,当二面角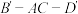 为直二面角时,求直四棱柱
为直二面角时,求直四棱柱 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
8 . 我们规定:在四面体 中,取其异面的两条棱的中点连线称为
中,取其异面的两条棱的中点连线称为 的一条“内棱”,三条内棱两两垂直的四面体称为“垂棱四面体”.
的一条“内棱”,三条内棱两两垂直的四面体称为“垂棱四面体”. 中,
中,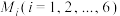 分别为所在棱的中点,证明:
分别为所在棱的中点,证明: 的三条内棱交于一点.
的三条内棱交于一点.
(2)同左图,若 为垂棱四面体,
为垂棱四面体,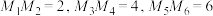 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(3)如右图,在空间直角坐标系中, 平面内有椭圆
平面内有椭圆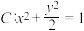 ,
, 为其下焦点,经过
为其下焦点,经过 的直线
的直线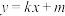 与
与 交于
交于 两点,
两点, 为
为 平面下方一点,若
平面下方一点,若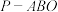 为垂棱四面体,则其外接球表面积
为垂棱四面体,则其外接球表面积 是
是 的函数
的函数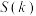 ,求
,求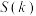 的定义域与最小值.
的定义域与最小值.
 中,取其异面的两条棱的中点连线称为
中,取其异面的两条棱的中点连线称为 的一条“内棱”,三条内棱两两垂直的四面体称为“垂棱四面体”.
的一条“内棱”,三条内棱两两垂直的四面体称为“垂棱四面体”.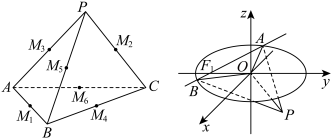
 中,
中,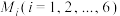 分别为所在棱的中点,证明:
分别为所在棱的中点,证明: 的三条内棱交于一点.
的三条内棱交于一点.(2)同左图,若
 为垂棱四面体,
为垂棱四面体,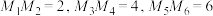 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.(3)如右图,在空间直角坐标系中,
 平面内有椭圆
平面内有椭圆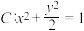 ,
, 为其下焦点,经过
为其下焦点,经过 的直线
的直线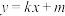 与
与 交于
交于 两点,
两点, 为
为 平面下方一点,若
平面下方一点,若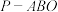 为垂棱四面体,则其外接球表面积
为垂棱四面体,则其外接球表面积 是
是 的函数
的函数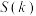 ,求
,求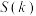 的定义域与最小值.
的定义域与最小值.
您最近一年使用:0次
9 . 如图,在直三棱柱 中,
中,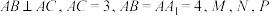 分别为
分别为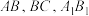 的中点.
的中点.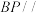 平面
平面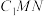 ;
;
(2)求二面角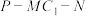 的余弦值.
的余弦值.
 中,
中,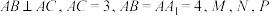 分别为
分别为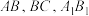 的中点.
的中点.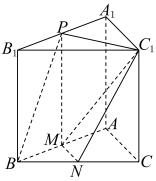
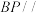 平面
平面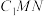 ;
;(2)求二面角
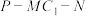 的余弦值.
的余弦值.
您最近一年使用:0次
解题方法
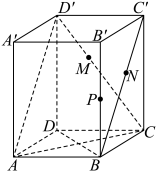
10 . 已知在长方体 中,
中,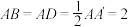 .
. 分别在线段
分别在线段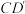 和
和 上,求
上,求 的最小值;
的最小值;
(2)若点 在棱
在棱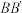 上运动,求直线
上运动,求直线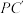 与平面
与平面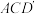 所成角的正弦值的最大值.
所成角的正弦值的最大值.
 中,
中,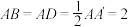 .
.
 分别在线段
分别在线段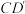 和
和 上,求
上,求 的最小值;
的最小值;(2)若点
 在棱
在棱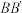 上运动,求直线
上运动,求直线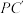 与平面
与平面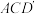 所成角的正弦值的最大值.
所成角的正弦值的最大值.
您最近一年使用:0次



