1 . 已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点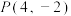 ,求直线l与圆M的方程.
,求直线l与圆M的方程.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点
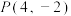 ,求直线l与圆M的方程.
,求直线l与圆M的方程.
您最近一年使用:0次
2017-08-07更新
|
12691次组卷
|
33卷引用:《高频考点解密》—解密18 圆与方程
(已下线)《高频考点解密》—解密18 圆与方程河南省焦作市博爱县第一中学2024届高三下学期开学摸底考试数学试题2017年全国普通高等学校招生统一考试理科数学(新课标3卷精编版)(已下线)《考前20天终极攻略》5月27日 直线与圆【理科】(已下线)《高频考点解密》—解密22 直线与圆锥曲线的位置关系2019届高考数学(理)全程训练:天天练32 圆的方程及直线与圆、圆与圆的位置关系人教A版高中数学 高三二轮(文)专题15 圆锥曲线的综合问题 测试浙教版高中数学 高三二轮 专题10 直线与圆锥曲线的基本问题 测试(已下线)专题9.10 第九章 平面解析几何(单元测试)(测)-浙江版《2020年高考一轮复习讲练测》河北省张家口市第一中学2018-2019学年高一衔接班下学期期末数学试题(已下线)秒杀题型07 圆锥曲线中的直角弦-2020年高考数学试题调研之秒杀圆锥曲线压轴题黑龙江省大庆市铁人中学2020届高三考前模拟训练(二)数学(文)试题(已下线)【新教材精创】2.4.1+圆的标准方程+B提高练-人教A版高中数学选择性必修第一册(已下线)考点25 直线与圆的综合问题-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)【新教材精创】2.3.1+圆的标准方程+B提高练-人教B版高中数学选择性必修第一册(已下线)专题28 抛物线-十年(2011-2020)高考真题数学分项江苏省南京市秦淮中学2020-2021学年高二上学期第一次段考数学试题(已下线)专题13 直线与圆-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)考点37 直线与圆的位置关系-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题54 圆锥曲线大题解题模板-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题9.4 直线与圆、圆与圆的位置关系-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题51 圆锥曲线大题解题模板-2021年高考一轮数学(文)单元复习一遍过(已下线)考点29 圆的方程-备战2022年高考数学(理)一轮复习考点微专题高中数学解题兵法 第八十三讲 集中力量,攻城略地(已下线)专题2.1 圆的方程-《讲亮点》2021-2022学年高二数学新教材同步配套讲练(苏教版2019选择性必修第一册)吉林省梅河口市第五中学2021-2022学年高二上学期第一次月考数学试题(已下线)专题19 圆锥曲线解答题沪教版(2020) 选修第一册 精准辅导 第2章 2.4(2) 抛物线的性质广东省佛山市顺德区华侨中学2024届高三上学期12月月考数学试题陕西省西安市西安中学2024届高三上学期期末数学(文)试题(已下线)第22题 代数几何比翼齐飞,动静互变化难为易(优质好题一题多解)(已下线)专题24 解析几何解答题(理科)-3专题37平面解析几何解答题(第二部分)
名校
2 . 已知过点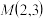 的直线l与抛物线E:
的直线l与抛物线E: 交于点A,B.
交于点A,B.
 若弦AB的中点为M,求直线l的方程;
若弦AB的中点为M,求直线l的方程;
 设O为坐标原点,
设O为坐标原点, ,求
,求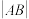 .
.
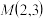 的直线l与抛物线E:
的直线l与抛物线E: 交于点A,B.
交于点A,B. 若弦AB的中点为M,求直线l的方程;
若弦AB的中点为M,求直线l的方程; 设O为坐标原点,
设O为坐标原点, ,求
,求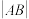 .
.
您最近一年使用:0次
2019-03-06更新
|
2032次组卷
|
8卷引用:【市级联考】河南省新乡市2018-2019学年高二上学期期末考试数学(文)试题
【市级联考】河南省新乡市2018-2019学年高二上学期期末考试数学(文)试题【市级联考】吉林省白山市2018-2019学年高二上学期期末联考数学(理)试题山西省临汾一中、翼城中学、曲沃中学等学校2018-2019学年高二上学期期末数学(文)试题安徽省滁州市九校2019-2020学年高二上学期期末考试数学(文)试题贵州省黔南州2018-2019学年高二上学期期末考试数学(文)试题山西省2018-2019学年高二上学期期末联合考试数学(理)试题(已下线)江西省南昌市2019-2020学年进贤二中高二下学期第一次月考数学(理)试题吉林省四平市第一高级中学2019-2020学年高二上学期第三次月考数学(文)试题
3 . 已知 为坐标原点,点
为坐标原点,点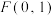 ,
, 为坐标平面内的动点,且2,
为坐标平面内的动点,且2,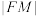 ,
, 成等差数列.
成等差数列.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)设点 的轨迹为曲线
的轨迹为曲线 ,过点
,过点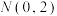 作直线
作直线 交曲线
交曲线 于
于 ,
, 两点,试问在
两点,试问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 为定值?若存在,求出定点
为定值?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 为坐标原点,点
为坐标原点,点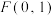 ,
, 为坐标平面内的动点,且2,
为坐标平面内的动点,且2,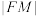 ,
, 成等差数列.
成等差数列.(1)求动点
 的轨迹方程;
的轨迹方程;(2)设点
 的轨迹为曲线
的轨迹为曲线 ,过点
,过点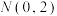 作直线
作直线 交曲线
交曲线 于
于 ,
, 两点,试问在
两点,试问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 为定值?若存在,求出定点
为定值?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
您最近一年使用:0次
2020-05-13更新
|
1016次组卷
|
5卷引用:2020届河南省开封市高三二模数学(理)试题
2020届河南省开封市高三二模数学(理)试题2020届河南省高三适应性测试理科数学试题河南省开封市2020届高三适应性测试理科数学(二模)试题商丘名校2022-2023学年高二上学期第一次联考数(理)试题(已下线)2.1+曲线与方程(2)(重点练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-1)
4 . 已知抛物线 上有三点
上有三点 ,
, ,
, ,
, 的垂心在
的垂心在 轴上,
轴上, ,
, 两点的纵坐标分别为
两点的纵坐标分别为 ,
, ,则点
,则点 的纵坐标为( )
的纵坐标为( )
 上有三点
上有三点 ,
, ,
, ,
, 的垂心在
的垂心在 轴上,
轴上, ,
, 两点的纵坐标分别为
两点的纵坐标分别为 ,
, ,则点
,则点 的纵坐标为( )
的纵坐标为( )A. | B. | C. | D. |
您最近一年使用:0次
2022-09-06更新
|
324次组卷
|
4卷引用:河南省名校联盟2022-2023学年高三上学期9月联考理科数学试题
5 . 过点 的直线与抛物线
的直线与抛物线 相交于
相交于 两点.
两点.
(1)求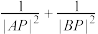 的值.
的值.
(2) 在直线
在直线 上的射影分别为
上的射影分别为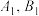 ,线段
,线段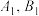 的中点为
的中点为 , 求证
, 求证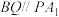 .
.
 的直线与抛物线
的直线与抛物线 相交于
相交于 两点.
两点.(1)求
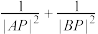 的值.
的值.(2)
 在直线
在直线 上的射影分别为
上的射影分别为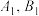 ,线段
,线段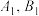 的中点为
的中点为 , 求证
, 求证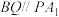 .
.
您最近一年使用:0次
6 . 已知抛物线 :
: 的焦点为
的焦点为 ,过
,过 作互相垂直的直线
作互相垂直的直线 ,
, 分别与
分别与 交于点
交于点 、
、 和
和 、
、 .
.
(1)当 的倾斜角为
的倾斜角为 时,求以
时,求以 为直径的圆的标准方程;
为直径的圆的标准方程;
(2)问是否存在常数 ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 :
: 的焦点为
的焦点为 ,过
,过 作互相垂直的直线
作互相垂直的直线 ,
, 分别与
分别与 交于点
交于点 、
、 和
和 、
、 .
.(1)当
 的倾斜角为
的倾斜角为 时,求以
时,求以 为直径的圆的标准方程;
为直径的圆的标准方程;(2)问是否存在常数
 ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
7 . 已知抛物线 的准线为
的准线为 ,
, 为
为 上一动点,过点
上一动点,过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为 .
.
(I)求证: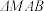 是直角三角形;
是直角三角形;
(II) 轴上是否存在一定点
轴上是否存在一定点 ,使
,使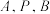 三点共线.
三点共线.
 的准线为
的准线为 ,
, 为
为 上一动点,过点
上一动点,过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为 .
.(I)求证:
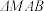 是直角三角形;
是直角三角形;(II)
 轴上是否存在一定点
轴上是否存在一定点 ,使
,使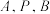 三点共线.
三点共线.
您最近一年使用:0次
2019-09-29更新
|
459次组卷
|
4卷引用:2019年河南省八市重点高中联盟高三9月“领军考试”数学(文)试题
2019年河南省八市重点高中联盟高三9月“领军考试”数学(文)试题2019年河南省八市重点高中联盟高三9月“领军考试”数学(理)试题2020届河南省八市重点高中联盟高三上学期“领军考试”数学(理)试题(已下线)专题9.9 圆锥曲线的综合问题(练)-浙江版《2020年高考一轮复习讲练测》
名校
解题方法
8 . 已知动圆 过定点
过定点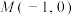 ,且圆心
,且圆心 到直线
到直线 的距离比
的距离比 大
大 .
.
(1)求动圆圆心 的轨迹
的轨迹 的方程;
的方程;
(2)已知轨迹 与直线
与直线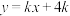 相交于
相交于 两点.试问,在
两点.试问,在 轴上是否存在一个定点
轴上是否存在一个定点 使得
使得 是一个定值?如果存在,求出定点
是一个定值?如果存在,求出定点 的坐标和这个定值;如果不存在,请说明理由.
的坐标和这个定值;如果不存在,请说明理由.
 过定点
过定点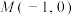 ,且圆心
,且圆心 到直线
到直线 的距离比
的距离比 大
大 .
.(1)求动圆圆心
 的轨迹
的轨迹 的方程;
的方程;(2)已知轨迹
 与直线
与直线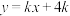 相交于
相交于 两点.试问,在
两点.试问,在 轴上是否存在一个定点
轴上是否存在一个定点 使得
使得 是一个定值?如果存在,求出定点
是一个定值?如果存在,求出定点 的坐标和这个定值;如果不存在,请说明理由.
的坐标和这个定值;如果不存在,请说明理由.
您最近一年使用:0次
9 . 动圆P与圆F:(x-2)2+y2=1外切,且与直线x=-1相切.
(1)求动圆的圆心P的轨迹C的方程;
(2)轨迹C上是否存在两点A,B关于直线y=x-1对称?若有,请求出两点的坐标,若没有,请说明理由.
(1)求动圆的圆心P的轨迹C的方程;
(2)轨迹C上是否存在两点A,B关于直线y=x-1对称?若有,请求出两点的坐标,若没有,请说明理由.
您最近一年使用:0次
解题方法
10 . 已知抛物线 (
( )的焦点为
)的焦点为 ,过
,过 作垂直于
作垂直于 轴的直线与抛物线
轴的直线与抛物线 交于
交于 ,
, 两点,
两点, 为坐标原点,
为坐标原点,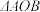 的面积为2.
的面积为2.
(1)求抛物线 的标准方程;
的标准方程;
(2)若直线 与抛物线
与抛物线 交于
交于 ,
, 两点,
两点, (3,2)是线段
(3,2)是线段 的中点,求直线
的中点,求直线 的方程.
的方程.
 (
( )的焦点为
)的焦点为 ,过
,过 作垂直于
作垂直于 轴的直线与抛物线
轴的直线与抛物线 交于
交于 ,
, 两点,
两点, 为坐标原点,
为坐标原点,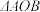 的面积为2.
的面积为2.(1)求抛物线
 的标准方程;
的标准方程;(2)若直线
 与抛物线
与抛物线 交于
交于 ,
, 两点,
两点, (3,2)是线段
(3,2)是线段 的中点,求直线
的中点,求直线 的方程.
的方程.
您最近一年使用:0次



