名校
解题方法
1 . 已知P(1,2)在抛物线C:y2=2px上.
(1)求抛物线C的方程;
(2)A,B是抛物线C上的两个动点,如果直线PA的斜率与直线PB的斜率之和为2,证明:直线AB过定点.
(1)求抛物线C的方程;
(2)A,B是抛物线C上的两个动点,如果直线PA的斜率与直线PB的斜率之和为2,证明:直线AB过定点.
您最近一年使用:0次
2022-04-07更新
|
5842次组卷
|
25卷引用:四川省南充市阆中市阆中中学校2021-2022学年高二下学期期中数学(文)试题
四川省南充市阆中市阆中中学校2021-2022学年高二下学期期中数学(文)试题河北省石家庄市第二中学2022届高三下学期高考考前模拟数学试题(已下线)考点22 抛物线-2-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)抛物线的综合问题(已下线)第二章 平面解析几何之圆锥曲线的方程(A卷·知识通关练)(6)新疆奇台县第一中学2022-2023学年高二上学期期中考试数学试题福建省厦门集美中学2022-2023学年高二上学期第三次月考数学试题河北省邢台市第一中学2022-2023学年高二上学期第三次月考数学试题(已下线)专题3.4 圆锥曲线的方程(基础巩固卷)-2022-2023学年高二数学必考点分类集训系列(人教A版2019选择性必修第一册)(已下线)第16讲 直线和圆锥曲线的位置关系(2)山西省运城市2021届高三下学期高考模拟(5月)数学(理)试题(已下线)3.3 抛物线-2021-2022学年高二数学链接教材精准变式练(苏教版2019选择性必修第一册)(已下线)3.3抛物线(A 基础培优练)-2021-2022学年高二数学同步双培优检测(苏教版2019选择性必修第一册)(已下线)专题15 《圆锥曲线的方程》综合测试卷--《2021--2022高二上学期数学新教材配套提升训练(人教A版2019选择性必修第一册)》(已下线)专题3.16 圆锥曲线中的定点、定值问题大题专项训练(30道)-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题29 抛物线(针对训练)-2023年高考一轮复习精讲精练宝典(新高考专用)陕西省咸阳市实验中学2021-2022学年高二上学期第三次月考文科数学试题山东省临沂市兰陵县第四中学2022-2023学年高二上学期期末数学试题广东省深圳市科学高中2022-2023学年高二上学期期末数学试题(已下线)3.3.2 抛物线的几何性质 (2)内蒙古自治区巴彦淖尔市衡越实验中学2022-2023学年高二下学期期中数学(理)试题(已下线)模块三 专题12 抛物线 B能力卷(已下线)模块三 专题15 抛物线 B能力卷(已下线)模块三 专题5 大题分类练(解析几何)基础夯实练 (已下线)艺体生一轮复习 第八章 解析几何 第41讲 抛物线【练】
2 . 已知抛物线C: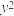 =2px经过点
=2px经过点 (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,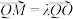 ,
,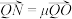 ,求证:
,求证: 为定值.
为定值.
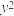 =2px经过点
=2px经过点 (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,
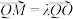 ,
,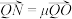 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2018-06-09更新
|
18180次组卷
|
57卷引用:四川省资阳市2022届高三二诊数学理科试题
四川省资阳市2022届高三二诊数学理科试题四川省泸县第五中学2022-2023学年高三上学期第三学月考试数学(理)试题四川省泸州市泸县第一中学2020-2021学年高三上学期开学考试数学(理)试题四川省泸州市泸县第一中学2020-2021学年高三上学期开学考试数学(文)试题(已下线)专题11 圆锥曲线-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)第46讲 范围、最值、定点、定值及探索性问题(讲) — 2022年高考数学一轮复习讲练测(课标全国版)四川省资阳市高中2021-2022学年高三上学期第二次诊断性考试数学(理)试题(已下线)第41讲 解析几何的同构问题-2022年新高考数学二轮专题突破精练(已下线)专题13解析几何中的定值、定点和定线问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题43 盘点圆锥曲线与平面向量交汇问题——备战2022年高考数学二轮复习常考点专题突破(已下线)专题44 盘点圆锥曲线中的定值问题——备战2022年高考数学二轮复习常考点专题突破广东省广州市执信中学2021-2022学年高二下学期期中数学试题浙江省杭州市2022-2023学年高三上学期期末模拟数学试题2018年全国普通高等学校招生统一考试理科数学(北京卷)(已下线)2018年高考题及模拟题汇编 【理科】6.解析几何【市级联考】江苏省南通市2019届高三阶段性学情联合调研数学试题(已下线)2018年11月18日 《每日一题》文数人教版一轮复习-每周一测【全国百强校】山西省祁县中学2018-2019学年高二上学期期末模拟一考试数学(理)试题【全国百强校】云南省玉溪一中2019届高三下学期第五次调研考试数学(文)试题(已下线)2019年6月16日 《每日一题》文数-每周一测湖北省荆门市两校2019-2020学年高三9月月考数学(文)试题(龙泉中学、宜昌一中)上海市青浦高级中学2018-2019学年高三上学期9月质量检测数学试题(已下线)专题9.9 圆锥曲线的综合问题(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题9.8 直线与圆锥曲线位置关系(练)-江苏版《2020年高考一轮复习讲练测》(已下线)专题9.7 抛物线(练)-江苏版《2020年高考一轮复习讲练测》(已下线)专题9.9 圆锥曲线的综合问题(讲)【理】-《2020年高考一轮复习讲练测》2019届重庆市第八中学校高考全真模拟理科数学试题2020届山西省大同四中联盟体高三3月模拟考试数学(理)试题安徽省六安市第一中学2019-2020学年高二下学期3月开学考试数学(理)试题(已下线)专题08 平面解析几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题18 解析几何综合-五年(2016-2020)高考数学(理)真题分项安徽省六安一中2019-2020学年高二(下)开学数学(理科)试题(已下线)专题9.9 圆锥曲线的综合问题(精讲)-2021年高考数学(理)一轮复习讲练测河北省唐山市第一中学2020-2021学年高二上学期期中数学试题(已下线)专题17 圆锥曲线中的椭圆问题-2021年高考数学二轮优化提升专题训练(新高考地区专用)【学科网名师堂】江苏省南通市海安高级中学2020-2021学年高二上学期第二次阶段检测数学试题(已下线)专题4.5 圆锥曲线-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)专题12 解析几何中的定值、定点和定线问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线) 专题22 圆锥曲线的“三定”与探索性问题(练)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题26 圆锥曲线的“三定”与探索性问题(练)-2021年高三数学二轮复习讲练测( 文理通用)内蒙古包头市第四中学2020-2021学年高三上学期期中考试数学(理)试题(已下线)考向36 圆锥曲线中的定点、定值问题(重点)(已下线)专题21 解析几何中的定点与定值问题江苏省常州市第一中学2022-2023学年高二上学期期末数学试题(已下线)专题9.9 圆锥曲线的综合问题(练)-浙江版《2020年高考一轮复习讲练测》(已下线)重组卷04第2章 圆锥曲线测试题 -2021-2022学年高二上学期数学北师大版(2019)选择性必修第一册人教B版(2019) 选修第一册 北京名校同步练习册 第二章 平面解析几何初步 本章测试(已下线)第五篇 向量与几何 专题5 调和点列 微点2 调和点列(二)(已下线)北京十年真题专题08平面解析几何北京十年真题专题08平面解析几何江西省南昌市第二中学2023-2024学年高二上学期期中考试数学试卷江西省新余市实验中学2023-2024学年高二上学期12月月考试数学试题(已下线)3.3.2 抛物线的简单几何性质【第三课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题08 圆锥曲线 第二讲 圆锥曲线中的定点、定直线与定值问题(分层练)(已下线)专题24 解析几何解答题(理科)-2专题12平面解析几何(第二部分)
名校
解题方法
3 . 已知抛物线的方程为 ,直线
,直线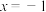 为抛物线的准线,点
为抛物线的准线,点 ,且
,且 为抛物线上的不同两点,若有
为抛物线上的不同两点,若有 与
与 垂直.
垂直.
(1)求抛物线的方程.
(2)证明:直线 过定点.
过定点.
 ,直线
,直线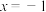 为抛物线的准线,点
为抛物线的准线,点 ,且
,且 为抛物线上的不同两点,若有
为抛物线上的不同两点,若有 与
与 垂直.
垂直.(1)求抛物线的方程.
(2)证明:直线
 过定点.
过定点.
您最近一年使用:0次
2023-11-19更新
|
1057次组卷
|
5卷引用:四川省凉山彝族自治州西昌市2022-2023 学年高二上学期期中检测文科数学试卷
11-12高二上·山东临沂·期末
名校
解题方法
4 . 已知抛物线 与直线
与直线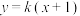 相交于A、B两点.
相交于A、B两点.
(1)求证: ;
;
(2)当 的面积等于
的面积等于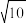 时,求k的值.
时,求k的值.
 与直线
与直线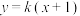 相交于A、B两点.
相交于A、B两点.(1)求证:
 ;
;(2)当
 的面积等于
的面积等于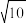 时,求k的值.
时,求k的值.
您最近一年使用:0次
2023-09-18更新
|
777次组卷
|
43卷引用:四川省广安市第二中学校2022-2023学年高二上学期11月期中考试数学(理)试题
四川省广安市第二中学校2022-2023学年高二上学期11月期中考试数学(理)试题四川省成都市锦江区田家炳中学2019-2020学年高二上学期期中数学理科试题沪教版(2020) 选修第一册 领航者 第2章 每周一练(3)(已下线)3.3抛物线A卷2023版 湘教版(2019) 选修第一册 过关斩将 第3章 3.3.2 抛物线的简单几何性质(已下线)第3章 圆锥曲线的方程【单元提升卷】(已下线)2010-2011学年山东省临沂第一中学高二上学期学业水平测试数学试卷(已下线)2011-2012学年黑龙江省緌棱县第一中学高二上学期期末考试文科数学(已下线)2012届陕西省西安中学高三第三次月考文科数学(普通班)(已下线)2013-2014学年山西太原第五中学高二12月月考文科数学试卷2015-2016学年宁夏育才中学高二上期末文科数学试卷2015-2016学年江西玉山一中高二下第一次月考文科数学卷2015-2016学年江西玉山一中高二下第一次月考文数学卷2015-2016学年甘肃省天水市秦安二中高二上学期期末文科数学试卷2016-2017北京西城14中高二上期中数学试题河北省定州市2017-2018学年高二上学期期中考试数学(理)试题吉林省梅河口市第五中学2017-2018学年高二上学期期末考试数学(文)试题2河北省阜城中学2017-2018学年高二上学期第六次月考数学(文)试题(已下线)2018年11月浙江省普通高中学业水平考试数学仿真模拟试题03【市级联考】广东省深圳市高级中学2018-2019学年高二上学期期中考试数学(文)试题【全国百强校】甘肃省天水市第一中学2018-2019学年高二上学期第二学段考试数学(文)试题【全国百强校】福建省厦门外国语学校2018-2019学年高二下学期期中考试数学(文)试题内蒙古自治区乌兰察布市集宁区内蒙古集宁一中2019-2020学年高二上学期12月月考数学(理)试题海南省海口市琼山区海南中学2019-2020学年高二上学期期中数学试题海南省海南中学2019-2020学年高二上学期期中考试数学试题人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.3 抛物线 3.3.2 抛物线的简单几何性质(已下线)专题51 椭圆、双曲线、抛物线(知识梳理)-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题51 椭圆、双曲线、抛物线(知识梳理)-2021年高考一轮数学(理)单元复习一遍过(已下线)考点51 直线与抛物线的位置关系(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)专题48 椭圆、双曲线、抛物线(知识梳理)-2021年高考一轮数学(文)单元复习一遍过湖南省衡阳市田家炳实验中学2020-2021学年高二上学期期中数学试题宁夏青铜峡市高级中学2020-2021学年高二上学期期末考试数学(文)试题安徽省滁州市定远县重点中学2020-2021学年高二上学期期末数学(文)试题黑龙江省哈尔滨市第六中学2020-2021学年高二下学期开学考试数学(理)试题(已下线)专题09 圆锥曲线的方程(同步练习)-(新教材)2020-2021学年高二数学单元复习(人教A版选择性必修第一册)第三章 (综合培优)圆锥曲线的方程 B卷-【双基双测】2021-2022学年高二数学同步单元AB卷(浙江专用)(人教A版2019选择性必修第一册)(已下线)课时3.3.2 抛物线(02)抛物线的简单几何性质-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)(已下线)河北省中等职业学校对口升学考试全真模拟冲刺卷数学试题十八吉林省乾安县第七中学2021-2022学年高二上学期期末考试数学试题湖南省衡阳市衡阳县第四中学2023-2024学年高二上学期11月期中数学试题(A卷)(已下线)模块一 专题4 圆锥曲线 期末终极研习室(2023-2024学年第一学期)高二人教A版(已下线)3.3.2 抛物线的简单几何性质【第一课】“上好三节课,做好三套题“高中数学素养晋级之路【课堂例】每周一练(3) 课堂例题 沪教版(2020)选择性必修第一册 第2章 圆锥曲线
名校
解题方法
5 . 设抛物线 的准线为l,A、B为抛物线上两动点,
的准线为l,A、B为抛物线上两动点,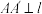 于
于 ,定点
,定点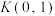 使
使 有最小值
有最小值 .
.
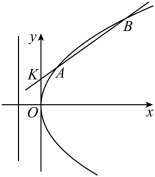
(1)求抛物线的方程;
(2)当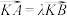 (
(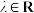 且
且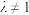 )时,是否存在一定点T满足
)时,是否存在一定点T满足 为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
 的准线为l,A、B为抛物线上两动点,
的准线为l,A、B为抛物线上两动点,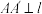 于
于 ,定点
,定点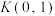 使
使 有最小值
有最小值 .
.
(1)求抛物线的方程;
(2)当
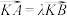 (
(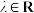 且
且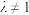 )时,是否存在一定点T满足
)时,是否存在一定点T满足 为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
您最近一年使用:0次
2022-12-04更新
|
1675次组卷
|
10卷引用:四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题
四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题四川省成都市成都市第七中学2022-2023学年高二上学期期中数学文科试题四川省成都市树德中学2022-2023学年高二上学期期中考试数学(理)试题云南省大理市下关第一中学教育集团2022~2023学年高二上学期段考(二)数学试题(A卷)云南省下关第一中学2022-2023学年高二上学期段考(二)数学(A卷)试题辽宁省沈阳市东北育才双语学校2022-2023学年高二上学期期末数学试题(已下线)专题04 圆锥曲线经典题型全归纳(2)广西壮族自治区南宁市第三中学2023届高三模拟数学(理)试题(二)湖南省长沙市长郡中学2023-2024学年高二上学期期中数学试题(已下线)3.3.2 抛物线的简单几何性质【第三课】“上好三节课,做好三套题“高中数学素养晋级之路
6 . 如图,已知点 是焦点为F的抛物线
是焦点为F的抛物线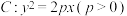 上一点,A,B是抛物线C上异于P的两点,且直线PA,PB的倾斜角互补,若直线PA的斜率为
上一点,A,B是抛物线C上异于P的两点,且直线PA,PB的倾斜角互补,若直线PA的斜率为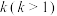 .
.
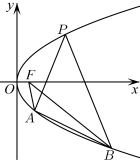
(1)求抛物线方程;
(2)证明:直线AB的斜率为定值并求出此定值;
(3)令焦点F到直线AB的距离d,求 的最大值.
的最大值.
 是焦点为F的抛物线
是焦点为F的抛物线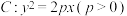 上一点,A,B是抛物线C上异于P的两点,且直线PA,PB的倾斜角互补,若直线PA的斜率为
上一点,A,B是抛物线C上异于P的两点,且直线PA,PB的倾斜角互补,若直线PA的斜率为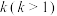 .
.
(1)求抛物线方程;
(2)证明:直线AB的斜率为定值并求出此定值;
(3)令焦点F到直线AB的距离d,求
 的最大值.
的最大值.
您最近一年使用:0次
2022-03-05更新
|
1452次组卷
|
4卷引用:四川省树德中学2021-2022学年高三下学期开学考试数学(文)试题
四川省树德中学2021-2022学年高三下学期开学考试数学(文)试题上海市控江中学2021-2022学年高二下学期期末数学试题(已下线)突破3.3 抛物线(课时训练)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)(已下线)3.3.2 抛物线的几何性质(难点)-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)
7 . 已知直线l: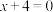 ,M为平面内一动点,过点M作直线l的垂线,垂足为N,且
,M为平面内一动点,过点M作直线l的垂线,垂足为N,且 (O为坐标原点).
(O为坐标原点).
(1)求动点M的轨迹E的方程;
(2)已知点P(0,2),直线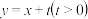 与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
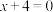 ,M为平面内一动点,过点M作直线l的垂线,垂足为N,且
,M为平面内一动点,过点M作直线l的垂线,垂足为N,且 (O为坐标原点).
(O为坐标原点).(1)求动点M的轨迹E的方程;
(2)已知点P(0,2),直线
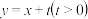 与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
您最近一年使用:0次
2022-04-19更新
|
1251次组卷
|
6卷引用:四川省宜宾市叙州区第一中学校2022届高三下学期高考适应性考试数学(文)试题
四川省宜宾市叙州区第一中学校2022届高三下学期高考适应性考试数学(文)试题四川省宜宾市叙州区第一中学校2022届高三下学期高考适应性考试数学(理)试题黑龙江省哈尔滨市第九中学校2022届高三下学期第三次模拟考试数学(理)试题(已下线)回归教材重难点04 圆锥曲线-【查漏补缺】2022年高考数学(理)三轮冲刺过关黑龙江省哈尔滨市第九中学校2022届高三第三次模拟考试数学(文科)试题(已下线)第10讲 高考难点突破二:圆锥曲线的综合问题(定值问题) (精讲)
解题方法
8 . 在平面直角坐标系xOy中,已知点 ,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.
,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.
(1)求C的方程;
(2)A、B是C上的两点,直线OA、OB的斜率分别为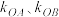 且
且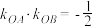 ,求证直线
,求证直线 过定点.
过定点.
 ,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.
,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.(1)求C的方程;
(2)A、B是C上的两点,直线OA、OB的斜率分别为
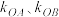 且
且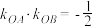 ,求证直线
,求证直线 过定点.
过定点.
您最近一年使用:0次
2022-07-15更新
|
1233次组卷
|
4卷引用:四川省遂宁市2021-2022学年高二下学期期末数学文科试题
名校
解题方法
9 . 已知点 ,直线
,直线 ,
, 为
为 轴右侧或
轴右侧或 轴上动点,且点
轴上动点,且点 到
到 的距离比线段
的距离比线段 的长度大1,记点
的长度大1,记点 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)已知直线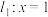 交曲线
交曲线 于
于 ,
, 两点(点
两点(点 在点
在点 的上方),
的上方), ,
, 为曲线
为曲线 上两个动点,且
上两个动点,且 ,求证:直线
,求证:直线 的斜率为定值.
的斜率为定值.
 ,直线
,直线 ,
, 为
为 轴右侧或
轴右侧或 轴上动点,且点
轴上动点,且点 到
到 的距离比线段
的距离比线段 的长度大1,记点
的长度大1,记点 的轨迹为
的轨迹为 .
.(1)求曲线
 的方程;
的方程;(2)已知直线
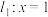 交曲线
交曲线 于
于 ,
, 两点(点
两点(点 在点
在点 的上方),
的上方), ,
, 为曲线
为曲线 上两个动点,且
上两个动点,且 ,求证:直线
,求证:直线 的斜率为定值.
的斜率为定值.
您最近一年使用:0次
2021-05-28更新
|
1926次组卷
|
9卷引用:四川省泸县第一中学2022-2023学年高三上学期期末考试数学(文)试题
四川省泸县第一中学2022-2023学年高三上学期期末考试数学(文)试题四川省泸县第一中学2022-2023学年高三上学期期末考试数学(理)试题四川省大数据精准联盟2021届高三第三次统一监测理科数学试题(已下线)专题21 圆锥曲线综合-备战2022年高考数学(理)母题题源解密(全国乙卷)2023版 北师大版(2019) 选修第一册 突围者 第二章 第四节 课时2 直线与圆锥曲线的综合问题抛物线的综合问题(已下线)3.3 抛物线-2021-2022学年高二数学链接教材精准变式练(苏教版2019选择性必修第一册)(已下线)3.3抛物线(A 基础培优练)-2021-2022学年高二数学同步双培优检测(苏教版2019选择性必修第一册)湖北省黄冈市学海园2024届高三下学期冲刺卷(一)数学试题
名校
解题方法
10 . 已知拋物线的顶点在原点,对称轴为  轴,且经过点
轴,且经过点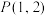 .
.
(1)求抛物线方程;
(2)若直线 与抛物线交于
与抛物线交于 两点,且满足
两点,且满足 ,求证: 直线
,求证: 直线 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
 轴,且经过点
轴,且经过点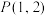 .
.(1)求抛物线方程;
(2)若直线
 与抛物线交于
与抛物线交于 两点,且满足
两点,且满足 ,求证: 直线
,求证: 直线 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
您最近一年使用:0次
2023-09-07更新
|
512次组卷
|
5卷引用:四川省盐亭中学2022-2023学年高二上学期期中数学(理)试题



