20-21高三上·陕西汉中·阶段练习
解题方法
1 . 已知椭圆 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合,且其离心率为
的焦点重合,且其离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)已知与坐标轴不垂直的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 ,求证:
,求证: (
( 为坐标原点)为定值.
为坐标原点)为定值.
 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合,且其离心率为
的焦点重合,且其离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)已知与坐标轴不垂直的直线
 与椭圆
与椭圆 交于
交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 ,求证:
,求证: (
( 为坐标原点)为定值.
为坐标原点)为定值.
您最近半年使用:0次
2023-08-07更新
|
1463次组卷
|
7卷引用:第3章 圆锥曲线与方程章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
(已下线)第3章 圆锥曲线与方程章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)(已下线)2.4.2直线与圆锥曲线的综合问题(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)模块四 专题6 大题分类练(圆锥曲线的方程)基础夯实练(人教A)陕西省汉中市2021届高三上学期第一次校际联考理科数学试题陕西省汉中市2021届高三上学期第一次校际联考文科数学试题(已下线)第八章 平面解析几何(测试)(已下线)信息必刷卷02
名校
解题方法
2 . 已知椭圆 :
: 的短轴长为
的短轴长为 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 的动直线
的动直线 与椭圆
与椭圆 相交于不同的
相交于不同的 两点,在线段
两点,在线段 上取点
上取点 ,满足
,满足 ,证明:点
,证明:点 总在某定直线上.
总在某定直线上.
 :
: 的短轴长为
的短轴长为 ,离心率为
,离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 的动直线
的动直线 与椭圆
与椭圆 相交于不同的
相交于不同的 两点,在线段
两点,在线段 上取点
上取点 ,满足
,满足 ,证明:点
,证明:点 总在某定直线上.
总在某定直线上.
您最近半年使用:0次
2023-08-04更新
|
1199次组卷
|
5卷引用:江苏省常州市田家炳高级中学2023届高三一模热身练习数学试题
江苏省常州市田家炳高级中学2023届高三一模热身练习数学试题江苏省徐州市2023-2024学年高二上学期期中数学试题江苏省连云港市灌云高级中学2024届高三上学期第一次月考数学试题(已下线)第三章 圆锥曲线的方程(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)(已下线)专题06 圆锥曲线大题
解题方法
3 . 已知椭圆 :
: 的右焦点为
的右焦点为 ,
, 为坐标原点,点
为坐标原点,点 为椭圆
为椭圆 上的两点,且
上的两点,且 ,
, 为
为 中点,则
中点,则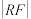 的最小值为( )
的最小值为( )
 :
: 的右焦点为
的右焦点为 ,
, 为坐标原点,点
为坐标原点,点 为椭圆
为椭圆 上的两点,且
上的两点,且 ,
, 为
为 中点,则
中点,则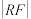 的最小值为( )
的最小值为( )A. | B.1 | C.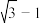 | D. |
您最近半年使用:0次
22-23高二上·广东珠海·期末
名校
解题方法
4 . 已知 为坐标原点,
为坐标原点,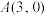 ,动点
,动点 满足
满足 ,记
,记 的轨迹为曲线
的轨迹为曲线 ,直线
,直线 的方程为
的方程为 ,
, 交
交 于两点
于两点 、
、 ,则下列结论正确的是( )
,则下列结论正确的是( )
 为坐标原点,
为坐标原点,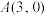 ,动点
,动点 满足
满足 ,记
,记 的轨迹为曲线
的轨迹为曲线 ,直线
,直线 的方程为
的方程为 ,
, 交
交 于两点
于两点 、
、 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 的方程为 的方程为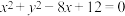 |
B. 的取值范围是 的取值范围是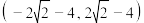 |
C.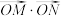 的最小值为8 的最小值为8 |
D. 可能是直角三角形 可能是直角三角形 |
您最近半年使用:0次
名校
解题方法
5 . 已知椭圆 的右焦点为
的右焦点为 ,上顶点为
,上顶点为 ,
, ,离心率为
,离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线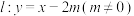 与椭圆
与椭圆 相交于
相交于 两点,且点
两点,且点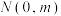 ,当
,当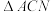 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
 的右焦点为
的右焦点为 ,上顶点为
,上顶点为 ,
, ,离心率为
,离心率为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
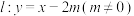 与椭圆
与椭圆 相交于
相交于 两点,且点
两点,且点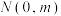 ,当
,当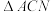 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
您最近半年使用:0次
2023-07-26更新
|
1296次组卷
|
13卷引用:江苏省扬州市宝应县2023-2024学年高二上学期期中数学试题
江苏省扬州市宝应县2023-2024学年高二上学期期中数学试题广西壮族自治区河池市2022-2023学年高二下学期期末教学质量检测数学试题广东省湛江市第一中学2024届高三上学期开学考试数学试题广东省潮州市潮安区凤塘中学2024届高三上学期统测(一)数学试题(已下线)高二上学期期中数学试卷(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)第三章 圆锥曲线的方程 章末测试(基础)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)第五节 椭圆 第二课时 直线与椭圆的位置关系 B素养提升卷广东省郁南县连滩中学2024届高三上学期9月月考数学试题(已下线)考点14 直线与圆锥曲线相交问题 2024届高考数学考点总动员【练】广东省汕尾市陆河县陆河外国语学校2023-2024学年高三上学期11月期中数学试题浙江省诸暨中学暨阳分校2023-2024学年高二上学期期中考试数学试题广东省惠州市博罗县博师高级中学2024届高三上学期9月月考数学试题安徽省合肥市庐江县2023-2024学年高二上学期第二次集体练习数学试题
22-23高二下·贵州黔西·期末
解题方法
6 . 已知 ,
, 分别为椭圆
分别为椭圆 :
: 的左,右顶点,椭圆
的左,右顶点,椭圆 过点
过点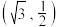 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若 为椭圆上异于
为椭圆上异于 ,
, 的一点,且直线
的一点,且直线 ,
, 分别与直线
分别与直线 :
: 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 ,证明:
,证明: ,
, ,
, 三点共线.
三点共线.
 ,
, 分别为椭圆
分别为椭圆 :
: 的左,右顶点,椭圆
的左,右顶点,椭圆 过点
过点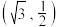 ,且离心率为
,且离心率为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若
 为椭圆上异于
为椭圆上异于 ,
, 的一点,且直线
的一点,且直线 ,
, 分别与直线
分别与直线 :
: 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 ,证明:
,证明: ,
, ,
, 三点共线.
三点共线.
您最近半年使用:0次
名校
解题方法
7 . 已知椭圆 ,圆
,圆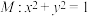 与x轴的交点恰为
与x轴的交点恰为 的焦点,且
的焦点,且 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 .
.
(1)求 的标准方程;
的标准方程;
(2)不过原点的动直线l与 交于
交于 两点,平面上一点
两点,平面上一点 满足
满足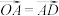 ,连接BD交
,连接BD交 于点E(点E在线段BD上且不与端点重合),若
于点E(点E在线段BD上且不与端点重合),若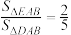 ,试判断直线l与圆M的位置关系,并说明理由.
,试判断直线l与圆M的位置关系,并说明理由.
 ,圆
,圆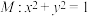 与x轴的交点恰为
与x轴的交点恰为 的焦点,且
的焦点,且 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 .
.(1)求
 的标准方程;
的标准方程;(2)不过原点的动直线l与
 交于
交于 两点,平面上一点
两点,平面上一点 满足
满足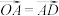 ,连接BD交
,连接BD交 于点E(点E在线段BD上且不与端点重合),若
于点E(点E在线段BD上且不与端点重合),若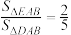 ,试判断直线l与圆M的位置关系,并说明理由.
,试判断直线l与圆M的位置关系,并说明理由.
您最近半年使用:0次
2023-07-09更新
|
535次组卷
|
9卷引用:江苏省连云港市新海高级中学2022-2023学年高二下学期6月月考数学试题
22-23高二下·湖南·期末
名校
解题方法
8 . 已知 为椭圆
为椭圆 上一点,且点
上一点,且点 在第一象限,过点
在第一象限,过点 且与椭圆
且与椭圆 相切的直线为
相切的直线为 .
.
(1)若 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为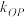 ,证明:
,证明: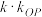 为定值,并求出该定值;
为定值,并求出该定值;
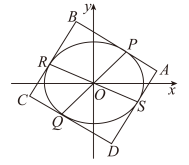
(2)如图,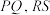 分别是椭圆
分别是椭圆 的过原点的弦,过
的过原点的弦,过 四点分别作椭圆
四点分别作椭圆 的切线,四条切线围成四边形
的切线,四条切线围成四边形 ,若
,若 ,求四边形
,求四边形 周长的最大值.
周长的最大值.
 为椭圆
为椭圆 上一点,且点
上一点,且点 在第一象限,过点
在第一象限,过点 且与椭圆
且与椭圆 相切的直线为
相切的直线为 .
.
(1)若
 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为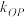 ,证明:
,证明: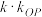 为定值,并求出该定值;
为定值,并求出该定值;(2)如图,
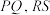 分别是椭圆
分别是椭圆 的过原点的弦,过
的过原点的弦,过 四点分别作椭圆
四点分别作椭圆 的切线,四条切线围成四边形
的切线,四条切线围成四边形 ,若
,若 ,求四边形
,求四边形 周长的最大值.
周长的最大值.
您最近半年使用:0次
2023-07-07更新
|
618次组卷
|
3卷引用:第3课时 课中 直线与椭圆的位置关系
22-23高二下·河南平顶山·期末
名校
解题方法
9 . 已知椭圆 经过点
经过点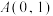 ,且离心率为
,且离心率为 .
.
(1)求椭圆E的方程;
(2)若经过点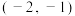 ,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
 经过点
经过点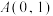 ,且离心率为
,且离心率为 .
.(1)求椭圆E的方程;
(2)若经过点
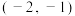 ,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
您最近半年使用:0次
2023-07-06更新
|
2006次组卷
|
8卷引用:3.1.2 椭圆的几何性质(2)
(已下线)3.1.2 椭圆的几何性质(2)河南省平顶山市2022-2023学年高二下学期期末数学试题湖南省长沙市第一中学2022-2023学年高二下学期期末数学试题(已下线)第20讲 椭圆的简单几何性质10种常见考法归类(2)(已下线)模块四 专题6 暑期结束综合检测6(能力卷)(已下线)第02讲 3.1.2椭圆的简单几何性质(2)(已下线)模块三 专题6 大题分类练(圆锥曲线)基础夯实练 期末终极研习室(高二人教A版)(已下线)专题03 椭圆13种常见考法归类(2)
2023·吉林白山·模拟预测
名校
解题方法
10 . 在xOy平面上,设椭圆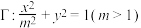 ,梯形ABCD的四个顶点均在
,梯形ABCD的四个顶点均在 上,且
上,且 .设直线AB的方程为
.设直线AB的方程为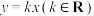
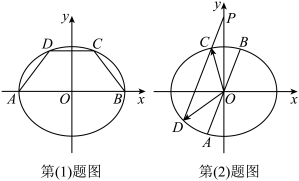
(1)若AB为 的长轴,梯形ABCD的高为
的长轴,梯形ABCD的高为 ,且C在AB上的射影为
,且C在AB上的射影为 的焦点,求m的值;
的焦点,求m的值;
(2)设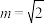 ,直线CD经过点
,直线CD经过点 ,求
,求 的取值范围;
的取值范围;
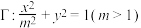 ,梯形ABCD的四个顶点均在
,梯形ABCD的四个顶点均在 上,且
上,且 .设直线AB的方程为
.设直线AB的方程为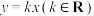

(1)若AB为
 的长轴,梯形ABCD的高为
的长轴,梯形ABCD的高为 ,且C在AB上的射影为
,且C在AB上的射影为 的焦点,求m的值;
的焦点,求m的值;(2)设
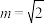 ,直线CD经过点
,直线CD经过点 ,求
,求 的取值范围;
的取值范围;
您最近半年使用:0次



